Контрольная работа по разделу 3.

Задание: оценить тесноту связи между переменными, используя все возможные коэффициенты тесноты связи.

Вариант 1

Возраст, лет	Основные категории потенциальных эмигрантов
	руководители	специалисты	служащие	рабочие
до 30	5	12	19	21
31-40	30	37	40	38
41-50	39	33	27	28
51 и более	26	18	14	13

Вариант 2

Стаж работы, лет	Категории сотрудников
	руководители	служащие	рабочие
до 5	10	11	176
5-10	7	23	216
10-15	5	24	131
15-20	3	20	120
20 и более	3	21	118

Вариант 3

Образование	Основные категории потенциальных эмигрантов
	Руководители	специалисты	служащие	рабочие
Высшее	55	48	12	7
Неполное высшее	5	3	3	5
Среднее специальное	36	44	51	39
Среднее общее	4	4	33	39
Неполное среднее	0	1	1	10

Вариант 4

Оценка Критерии преподавателя оценки качества преподавателя	Высокая	Средняя	Низкая	Затруднялись ответить
Знание предмета	62	26	1	11
Умение обучать	21	61	8	10
Восприимчивость к новому	20	51	10	19
Способность к саморазвитию	25	51	10	14

Вариант 5

Тип школы	Хорошее освоение курса (тыс.чел)	Среднее освоение курса (тыс.чел)	Проблемы с освоением курса (тыс.чел)
А	85,0	11,2	3,8
В	79,3	10,7	9,4
С	61,5	17,6	20,3

Вариант 6

Регион	цена товара, руб
	июнь	июль
1	12	13
2	17	19

Вариант 7

Регион	объем продаж, шт
	июль	август
1	10000	18000
2	20000	9000

Вариант 8

Вид изделия	Произведено, шт.
	январь	февраль
А	458	450
Б	311	324
В	765	752

Вариант 9

Вид изделия	Затраты времени на 1 изделие, чел.-ч
	январь	февраль
А	1,0	0,9
Б	1,2	1,0
В	0,9	0,8

Вариант 10

Мнения респондентов о вероятности увольнения	Рабочие
	Государственные предприятия	кооперативы
Очень вероятно	55	48
Практически исключено	45	52

Вариант 11

Источник средств	Зарождающийся бизнес	Зрелый бизнес
Банковский кредит	31	32
Собственные средства	38	15

Вариант 12

Форма собственности предприятия	Удовлетворенность уровнем жизни
	вполне удовлетворен	не удовлетворен
Государственная	30	55
Частная	10	5

Вариант 13

Основные категории потенциальных эмигрантов	Возраст, лет
	до 30	30-40	40-50	50 и более
	25	35	45	55
Руководители	5	30	39	26
Рабочие	21	38	28	13

Вариант 14

Форма собственности предприятия	Оценка уровня жизни респондентов
	вполне удовлетво-рительная	скорее удовлетво-рен	скорее не удовлетво-рен	совсем не удовлетво-рен
Государственная	31	35	35	35
Муниципальная	17	13	14	9
Смешанная российская	4	2	1	1
Частная	8	5	4	3

Вариант 15

Группы потребителей наркотиков	Семейное положение
	замужем (женат)	не замужем (не женат)
Потреблял	10,0	14,5
Не потреблял	2,5	4,5

Контрольные вопросы по разделу 3.

1. Понятие категориальных данных.

2. Коэффициент корреляции Спирмена.

3. Коэффициент корреляции Юла.

4. Фи-коэффициент и V-коэффициент.

5. Коэффициент корреляции Чупрова.

6. Анализ двухвходовых таблиц .

Методические указания к решению задач по разделу 4.

Экономические данные (со статистической точки зрения) обычно делятся на два вида: перекрестные данные и временные ряды.

Перекрестные данные – это данные по какому – либо экономическому показателю, полученные для разных однотипных объектов (предприятий, фирм, регионов и т.д.). При этом либо все данные относятся к одному и тому же времени, либо их временная принадлежность несущественна.

Временные данные – это последовательность измерений в последовательные моменты времени. В отличие от анализа перекрестных данных анализ временных рядов основывается на предположении, что последовательные значения в наборе данных наблюдаются через равные промежутки времени. Анализ временных рядов включает широкий спектр разведочных процедур и исследовательских методов, которые ставят две основные цели: определение природы временного ряда и предсказание будущих значений временного ряда по настоящим и прошлым значениям (прогнозирован6ие). Обе эти цели требуют, чтобы модель была идентифицирована и более или менее формально описана.

Как и большинство других видов анализа, анализ временных рядов предполагает, что данные содержат систематическую составляющую (обычно включающую несколько компонент) и случайную ошибку, которая затрудняет обнаружение регулярных компонент. Обычно модель временного ряда представляют следующим образом: , гдеtr – это трендовая составляющая, а s – сезонная компонента. e – это случайная ошибка.

Тренд – это основная тенденция развития процесса во времени.

Существует достаточно большое число методов для выделения тренда. Широкое распространение получили метод наименьших квадратов (принципы метода рассмотрены ранее) и метод разностных операторов, для выделения сезонной компоненты – метод сезонного оператора, для выделения тренда – метод скользящей средней.

Рассмотрим метод выделения тренда более подробно.

Подбор адекватной функции тренда осуществляется с помощью метода наименьших квадратов. Для оценивания построенной модели используют R². В практике статистического изучения временных рядов различают следующие основные типы развития явлений во времени:

1. равномерное развитие – развитие с постоянным абсолютным приростом уровней временного ряда. Основная тенденция развития описывается линейным типом тренда: 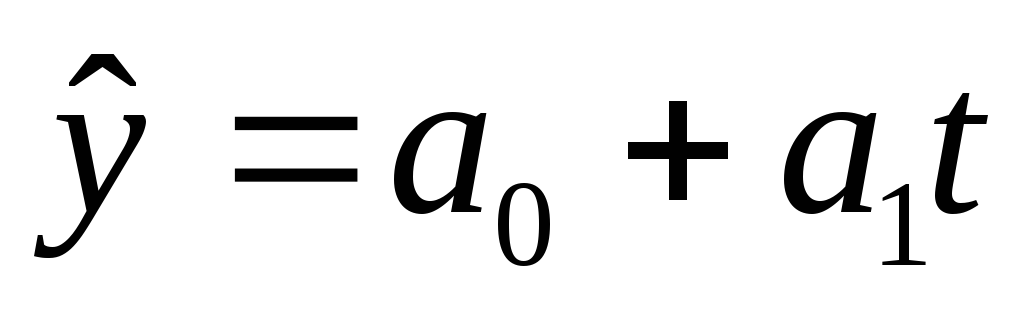, гдеa₀ – постоянная составляющая, a₁ – коэффициент, характеризующий скорость (темп) развития изучаемого процесса и направление его развития (при a₁>0 уровни динамики равномерно возрастают, при a₁<0 – равномерно снижаются).

2. равноускоренное (равнозамедленное) развитие – развитие при постоянном увеличении (замедлении) темпа прироста уровней временного ряда. Основная тенденция развития описывается полиномом второй степени: 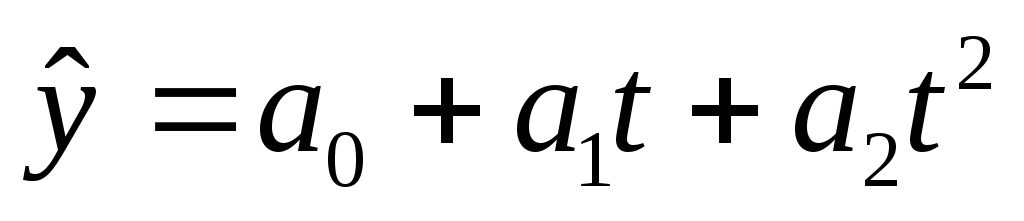, гдеa₂ – коэффициент, характеризующий постоянное изменение скорости (темпа) развития (при a₂>0 происходит ускорение развития, при a₂<0 – замедление развития).

3. развитие с переменным ускорением (замедлением) – развитие при переменном увеличении (замедлении) темпа прироста уровней временного ряда. Основная тенденция описывается полиномом третьей степени: , гдеa₃ – коэффициент, характеризующий изменение ускорения развития (при a₃>0 ускорение возрастает, при a₃<0 – замедление развития).

4. развитие с замедлением роста в конце периода – развитие, при котором прирост в конечных уровнях временного ряда стремиться к нулю. Основная тенденция описывается логарифмической функцией

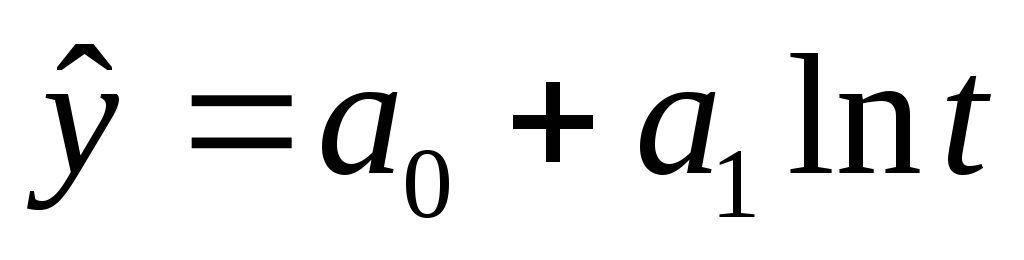
Отметим, что пользоваться трендовыми моделями для краткосрочных и среднесрочных прогнозов следует только при выполнении следующих условий:

• период времени, за который изучается прогнозируемый процесс, должен быть достаточным для выявления закономерностей;

• трендовая модель в анализируемый период должна развиваться эволюционно;

• процесс, описываемый временным рядом, должен обладать определенной инерционностью, т.е. для наступления большого изменения в поведении процесса необходимо значительное время;

• влияние более поздней информации должно сильнее отражаться на прогнозируемой оценке, чем влияние более ранней информации.

В Microsoft Excel трендовые модели строятся на основе диаграмм, представляющих уровни динамики. Для эмпирического временного ряда может быть построена диаграмма одного из следующих типов: гистограмма, линейчатая диаграмма, график, точечная диаграмма, диаграмма с областями.

Для построения линии тренда необходимо выделить временной ряд и выбрать в контекстном меню (вызывается щелчком правой клавиши мыши) команду Добавить линию тренда. Будет вызвано диалоговое окно Линия тренда, содержащее вкладку Тип, на которой задается тип тренда:

1. линейный;

2. логарифмический;

3. полиномиальный (от 2-ой до 6-ой степени включительно);

4. степенной;

5. экспоненциальный;

6. скользящее среднее (с указанием периода сглаживания от 2 до 15). Этот тип будет рассмотрен позднее.

Вкладка Параметры предназначена для задания параметров тренда.

Наряду с линией тренда на графике так же могут быть отражены планки погрешностей. Планки погрешностей представляют собой доверительные области.

Задача 1. Требуется по данным о розничном товарообороте региона построить трендовую модель товарооборота.

Исходные данные:

Год	Объем розничного товарооборота, млрд руб.	Темп роста по годам, %	Абсолютный прирост по годам, млрд руб.
1985	16,4	-	-
1986	17,05	104,0	0,65
1987	17,24	101,1	0,19
1988	18,57	107,7	1,33
1989	19,08	102,7	0,51

Разнохарактерность темпов роста и значительная колеблемость цепных абсолютных приростов наталкивают на мысль, что развитие изучаемого процесса происходит с переменным ускорением, т.е. его основная тенденция описывается полиномом 3-го порядка:

. Однако данная гипотеза требует количественного подтверждения, для чего необходимо осуществить перебор решений по намеченным типам математических функций.

Для нахождения адекватного уравнения тренда используем инструмент "Подбор линии тренда" из мастера диаграмм Microsoft Excel. Результаты подбора приведены в таблице:

Вид уравнения	Уравнение	Коэффициент детерминации,R2
Линейное	y=0.688x+15,604	0,9504
Логарифмическое	y=1,6245Ln(x)+16,113	0,8561
Полином второго порядка	y=0,0614x2+0,3194x+16,034	0,9610
Полином третьего порядка	y=-0.03x3+0,3314x2-0,3886x+16,538	0,9636
Степенное	y=16,152x0.0921	0,8671
Экспоненциальное	y=15,701e0,0388x	0,9538

График наиболее подходящей линии тренда:

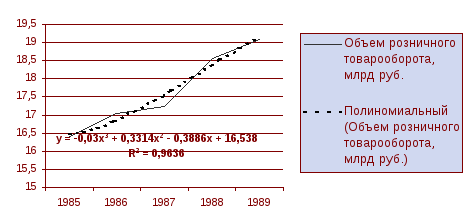
Таким образом, принимая во внимание физическую сущность изучаемого процесса и результаты проведенного аналитического построения (см. таблицу), в качестве модели тренда выбираем полином 3-го порядка.

Метод скользящей средней

Это один из самых старых и широко известных способов сглаживания временного ряда. Сглаживание представляет собой некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Так, метод скользящей средней основан на переходе от начальных значений ряда к их средним значениям на интервале времени, длина которого выбрана заранее (данный интервал времени часто называют "окном"). При этом сам выбранный интервал скользит вдоль ряда.

Получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд, за счет усреднения отклонений исходного ряда. Таким образом, эта процедура дает представление об общей тенденции поведения ряда. Ее применение особенно полезно для рядов с сезонными колебаниями и неясным характером тренда.

Формальное определение метода скользящей средней для окна сглаживания, длина которого выражается нечетным числом p=2m+1. Пусть имеются измерения во времени: y₁, y₂…y_n.

Тогда метод скользящей средней состоит в том, что исходный временной ряд преобразуется в ряд сглаженных значений (оценок) по формуле:

, где р – размер окна, j – порядковый номер уровня в окне сглаживания, m – величена, определяемая по формуле: m = (p-1) / 2.

При применении метода скользящей средней выбор размера окна сглаживания p должен осуществляться исходя из соображений и привязанности к периоду сезонности для сезонных волн. Если процедура скользящего среднего используется для сглаживания не сезонных рядов, то окно выбирают равным трем, пяти или семи. Чем больше размер окна, тем более гладкий вид имеет график скользящих средних.

Задача 2. На основе данных о производстве стиральных машин фирмой за 15 месяцев 2002-2003 гг. нужно произвести сглаживание ряда методом трехчленной скользящей средней.

Месяц	Стиральные машины, тыс. шт.	Трехчленные скользящие суммы	Трехчленные скользящие средние
1	155	-	-
2	163	-	161,7
3	167	485	153,7
4	131	461	152,0
5	158	456	145,3
6	147	436	145,0
7	130	435	140,7
8	145	422	134,3
9	128	403	137,7
10	140	413	142,3
11	159	427	153,0
12	160	459	155,3
13	147	466	152,3
14	150	457	154,0
15	165	462	-

Взяв данные за первые три месяца, исчисляем трехчленные суммы, а затем среднюю:

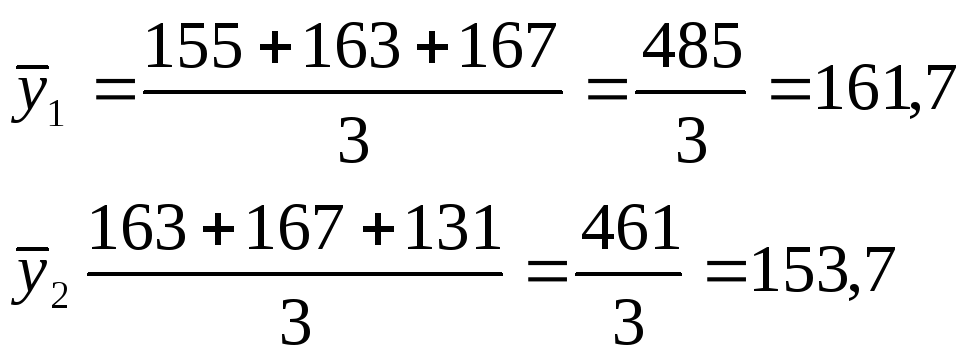и т.д.

Для реализации процедуры скользящей средней можно воспользоваться функцией Microsoft Excel. В закладке "Анализ данных" выбираем "скользящее среднее". Этот режим работы служит для сглаживания уровней временного ряда на основе метода простой скользящей средней. Указывается интервал – т.е. размер окна сглаживания. По умолчанию р=3.

Получаем на выходе следующий результат:

Месяц	Стиральные машины, тыс. шт.	Трехчленные скользящие средние, полученные с помощью инструмента "Скользящее среднее"	Трехчленные скользящие средние, полученные выше вручную
1	155	-	-
2	163	161,6667	161,7
3	167	153,6667	153,7
4	131	152	152
5	158	145,3333	145,3
6	147	145	145
7	130	140,6667	140,7
8	145	134,3333	134,3
9	128	137,6667	137,7
10	140	142,3333	142,3
11	159	153	153
12	160	155,3333	155,3
13	147	152,3333	152,3
14	150	154	154
15	165	-	-

На графике отображен исходный ряд и сглаженный. Теперь для сглаженного ряда проще и точнее можно определить основную тенденцию (например, подобрать линию тренда).