
- •Институт «высшие столыпинские курсы» государственного права и управления
- •Пояснительная записка
- •Студенты также должны иметь представление:
- •Учебно-тематический план по курсу: «Эконометрика»
- •Программа курса
- •Методические указания к решению задач по разделу 1.
- •3. Коэффициент корреляции
- •Решение
- •Контрольная работа по разделу 1.
- •Методические указания к решению задач по разделу 2.
- •Задача 4.
- •Методические указания к решению задач по разделу 3.
- •Коэффициент ранговой корреляции Спирмена.
- •Коэффициент "" Кендалла
- •Анализ двухвходовых таблиц ""
- •Фи-коэффициент
- •Коэффициент сопряженности признаков
- •V – коэффициент Крамера.
- •Коэффициент взаимной сопряженности Чупрова
- •Контрольная работа по разделу 3.
- •Анализ сезонных колебаний
- •Контрольные вопросы для самопроверки по разделу 4.
- •Контрольная работа по разделу 4.
- •Список рекомендуемой литературы
- •I Список рекомендуемой литературы.
Анализ сезонных колебаний
При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по временным периодам: годам, кварталам, месяцам, неделям. Гармонический тренд – один из способов представления сезонных явлений.
Формального математического определения сезонности нет, но зато есть огромное количество всевозможных практических примеров проявления сезонности (например, спрос на меховые шапки подвержен сезонным колебаниям, количество пересылаемых по почте писем также связано с сезонностью – в конце каждого квартала организации пересылают по почте свою отчетность в налоговые инспекции). В сезонности выделяют 2 параметра, которые необходимо оценить – период и форму.
Замечание: для выявления сезонности не обязательно производить наблюдения строго периодически.
Для выявления сезонных колебаний обычно анализируются месячные, годовые и квартальные уровни ряда динамики за год или за несколько лет. При изучении сезонных колебаний используются модели сезонных волн. Например, в следующем виде:
![]() где
k
– определяет гармонику тригонометрического
многочлена,
где
k
– определяет гармонику тригонометрического
многочлена,
t – время.
![]() T
– объем выборки.
T
– объем выборки.
Целью гармонического анализа является выявление и измерение периодических колебаний во временных ряда. Это уравнение представляет собой ряд Фурье. Обычно высчитывают не более четырех гармоник.
Введем
понятия частота
![]() ипериод
ипериод
![]() k-й
гармоники
k-й
гармоники
Будем
строить регрессоры из функций вида
![]() и
и![]() в соответствие с вышеуказанной идеей
– т.е. необходимо построитьT
линейно независимых регрессоров.
в соответствие с вышеуказанной идеей
– т.е. необходимо построитьT
линейно независимых регрессоров.
На
практике описанное выше представление
очень громоздко, пользоваться им нельзя.
Оно нужно для того, чтобы построить т.н.
спектрограмму.
Сначала ищутся оценки всех коэффициентов
в сумме. Тогда значения спектрограммы
![]() Спектрограмма – это графикrk
относительно частот.
Спектрограмма – это графикrk
относительно частот.
Пики спектрограммы соответствуют частотам, вносящим наиболее яркий и значимый вклад в прогноз. Наибольшая частота на графике спектрограмме всегда = ½, это максимальная частота, различимая при дискретных по времени наблюдениях.
Спектрограмма позволяет связать теорию рядов Фурье с практикой прогнозирования. Она дает возможность оценить те частоты, которые вносят наибольший вклад, т.е. аппроксимировать громоздкую сумму разложения Фурье. Иногда ее удается сократить до 2-3 слагаемых.
Замечание: на графике спектрограммы следует выделить не только частоты, соответствующие пикам, но и близкие к ним частоты. В соответствии с общей методологией анализа лучше сначала взять больше частот, чем нужно, а затем исключить избыточные.
Модель ряда с гармоническим трендом:
 ,
,
![]() -
наиболее значимые частоты.
-
наиболее значимые частоты.
Как и полиномиальные тренды, гармонические сводятся к модели линейной регрессии
![]()
![]()
![]()
Время (t) выражается в радиальной мере или градусах:
|
Месяцы (t) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Радиальная мера |
0 |
π/6 |
π/3 |
π/2 |
2π/3 |
5π/6 |
π |
7π/6 |
4π/3 |
3π/2 |
5π/3 |
11π/6 |
|
Градусы |
0 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
320 |
|
Уровни
( |
|
|
|
|
|
|
|
|
|
|
|
|
Эта процедура перехода от номеров времени к градусам называется преобразованием Фурье.
Задача 3. По данным о продаже картофеля на рынках сельхозпродуктов города проанализировать сезонные колебания продаж.
Данные и промежуточные результаты представлены в таблице:
|
Месяц, t |
Продано, y |
ycost |
ysint |
|
|
1 |
30 |
30,0 |
0 |
35,60 |
|
2 |
40 |
36,64 |
20 |
40,51 |
|
3 |
43 |
21,5 |
37,24 |
45,11 |
|
4 |
54 |
0 |
54,00 |
48,03 |
|
5 |
67 |
-33,5 |
58,02 |
48,55 |
|
6 |
29 |
-25,11 |
14,5 |
46,53 |
|
7 |
35 |
-35,00 |
0 |
42,52 |
|
8 |
34 |
-29,44 |
-17,00 |
38,25 |
|
9 |
45 |
-22,50 |
-38,97 |
33,05 |
|
10 |
35 |
0 |
-35,00 |
30,13 |
|
11 |
29 |
14,50 |
-25,11 |
29,61 |
|
12 |
28 |
24,25 |
-14,00 |
31,63 |
|
Итого |
469 |
-20,66 |
53,68 |
469,52 |
На основе полученных итогов данных таблицы находим:
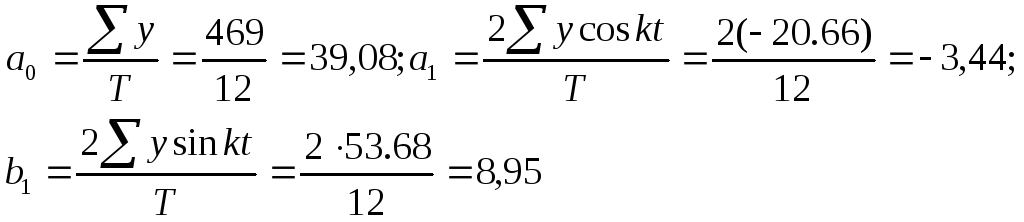
Отсюда
![]() Подставляя
в это уравнение значенияcost
и sint,
получаем теоретические значения
количества проданного картофеля
Подставляя
в это уравнение значенияcost
и sint,
получаем теоретические значения
количества проданного картофеля
![]() .
.
Параметры гармоник второго и высшего порядка рассчитываются аналогично, и их значения последовательно присоединяются к значениям первой гармоники.
Например, опуская расчеты, запишем уравнение для нашего ряда с учетом второй гармоники:
![]() Подставив
в это уравнение значения cos2t
и sin2t,
получим значения
Подставив
в это уравнение значения cos2t
и sin2t,
получим значения![]() по месяцам. Сравнив эти две модели с
помощью, например,R2,
можно сделать вывод, какая гармоника
ряда Фурье близка к фактическим уровням
ряда.
по месяцам. Сравнив эти две модели с
помощью, например,R2,
можно сделать вывод, какая гармоника
ряда Фурье близка к фактическим уровням
ряда.
Для уменьшения времени вычисления преобразования Фурье разработан алгоритм, получивший название быстрого преобразования Фурье. Это преобразование реализовано в Microsoft Excel. Однако у этой процедуры есть один существенный недостаток: входной интервал должен содержать число значений, равных степени 2. Один из способов преодоления данного недостатка – добавление в ряд констант (например, нулей) до тех пор, пока длина ряда не станет равной степени 2.
Задача 4. Даны данные о динамике урожайности зерновых культур в одном из хозяйств области.
|
Год |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
Урожайность |
17,6 |
18,1 |
17,4 |
16,8 |
16 |
15,4 |
14 |
16,6 |
|
Год |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
|
Урожайность |
14,4 |
14,2 |
14,6 |
13,8 |
13,4 |
14,2 |
13,2 |
13,2 |
Решение
задачи начнем с построения трендовой
модели ряда. В Microsoft
Excel
данную операцию удобнее всего проводить
с помощью инструмента "Подбор
линии тренда"
из мастера диаграмм. Анализ трендовых
моделей показывает, что в качестве
рабочей модели модно выбрать линейную
модель:
![]() .
Такой выбор обусловлен тем, что, во-первых,
коэффициент детерминацииR2=0,82
имеет достаточно высокое значение (
лишь очень незначительно уступает
коэффициенту детерминации R2=0,85
для полинома 2-го порядка); во-вторых,
все коэффициенты модели значимы;
в-третьих, при прочих равных условиях
данная модель наиболее проста для
вычислений и наиболее "прозрачна"
для последующей экономической
интерпретации.
.
Такой выбор обусловлен тем, что, во-первых,
коэффициент детерминацииR2=0,82
имеет достаточно высокое значение (
лишь очень незначительно уступает
коэффициенту детерминации R2=0,85
для полинома 2-го порядка); во-вторых,
все коэффициенты модели значимы;
в-третьих, при прочих равных условиях
данная модель наиболее проста для
вычислений и наиболее "прозрачна"
для последующей экономической
интерпретации.
График уравнения тренда показан на рисунке:

Для более детального анализа построенной модели можно использовать режим "Регрессия". Показатели, рассчитанные в данном режиме, представлены в таблице:
|
ВЫВОД ИТОГОВ |
|
|
|
|
|
| ||||
|
Регрессионная статистика |
|
|
|
|
| |||||
|
Множественный R |
0,907548626 |
|
|
|
|
| ||||
|
R-квадрат |
0,823644509 |
|
|
|
|
| ||||
|
Нормированный R-квадрат |
0,811047688 |
|
|
|
|
| ||||
|
Стандартная ошибка |
0,726020725 |
|
|
|
|
| ||||
|
Наблюдения |
16 |
|
|
|
|
| ||||
|
Дисперсионный анализ |
|
|
|
|
| |||||
|
|
df |
SS |
MS |
F |
Значимость F |
| ||||
|
Регрессия |
1 |
34,4648897 |
34,46489 |
65,3851 |
1,21E-06 |
| ||||
|
Остаток |
14 |
7,37948529 |
0,527106 |
|
|
| ||||
|
Итого |
15 |
41,844375 |
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% | ||||
|
Y-пересечение |
17,8875 |
0,38072848 |
46,9823 |
8,3E-17 |
17,0709 |
18,7040 | ||||
|
t |
-0,318382353 |
0,03937400 |
-8,08611 |
1,21E-06 |
-0,4028 |
-0,2339 | ||||
|
ВЫВОД ОСТАТКА |
|
|
| |||||||
|
Наблюдение |
Предсказан- ное Урожайность |
Остатки |
| |||||||
|
1 |
17,56911765 |
0,03088235 |
| |||||||
|
2 |
17,25073529 |
0,84926470 |
| |||||||
|
3 |
16,93235294 |
0,46764705 |
| |||||||
|
4 |
16,61397059 |
0,18602941 |
| |||||||
|
5 |
16,29558824 |
-0,2955882 |
| |||||||
|
6 |
15,97720588 |
-0,5772058 |
| |||||||
|
7 |
15,65882353 |
-1,6588235 |
| |||||||
|
8 |
15,34044118 |
1,25955882 |
| |||||||
|
9 |
15,02205882 |
-0,6220588 |
| |||||||
|
10 |
14,70367647 |
-0,5036764 |
| |||||||
|
11 |
14,38529412 |
0,21470588 |
| |||||||
|
12 |
14,06691176 |
-0,2669117 |
| |||||||
|
13 |
13,74852941 |
-0,3485294 |
| |||||||
|
14 |
13,43014706 |
0,76985294 |
| |||||||
|
15 |
13,11176471 |
0,08823529 |
| |||||||
|
16 |
12,79338235 |
0,40661764 |
| |||||||
Столбец Остатки содержит значения отклонений от основной тенденции (разность между эмпирическими и теоретическими значениями). Гармонический анализ проведем с помощью режима "Анализ Фурье" для остатков. Тогда мы построим обобщенный тренд, описывающий в наших данных и основную тенденцию, и сезонности.
Результат применения режима работы указан в таблице.
|
Остатки |
Y |
Действительная часть, Yd |
Мнимая часть, Ym |
|
|
|
|
R2 |
|
0,0308823 |
0 |
0 |
|
a0 |
0,00 |
|
|
0,0000 |
|
0,8492647 |
3,2179246833565+0,985461907212836i |
3,217925 |
0,985 |
a1 |
0,20 |
b1 |
0,06 |
0,0442 |
|
0,4676470 |
1,39644406072503-1,12572977822617i |
1,396444 |
-1,126 |
a2 |
0,09 |
b2 |
-0,07 |
0,0126 |
|
0,1860294 |
-2,2329138282402-1,2706916705285i |
-2,23291 |
-1,271 |
a3 |
-0,14 |
b3 |
-0,08 |
0,0258 |
|
-0,2955882 |
-0,3470588235293 +1,0470588235294i |
-0,34706 |
1,047 |
a4 |
-0,02 |
b4 |
0,07 |
0,0048 |
|
-0,5772058 |
0,71036905643527-3,48957546372124i |
0,710369 |
-3,490 |
a5 |
0,04 |
b5 |
-0,22 |
0,0495 |
|
-1,6588235 |
-1,2905617077838 +3,3801525747150i |
-1,29056 |
3,380 |
a6 |
-0,08 |
b6 |
0,21 |
0,0511 |
|
1,2595588 |
0,916384794330886-1,02165718009751i |
0,916385 |
-1,022 |
a7 |
0,06 |
b7 |
-0,06 |
0,0074 |
|
-0,6220588 |
-4,2470588235294 |
-4,24706 |
0,000 |
a8 |
-0,27 |
b8 |
0,00 |
0,0705 |
|
-0,5036764 |
0,916384794330889+1,0216571800975I |
0,916385 |
1,022 |
a9 |
0,06 |
b9 |
0,06 |
0,0074 |
|
0,2147058 |
-1,2905617077838-3,38015257471502i |
-1,29056 |
-3,380 |
a10 |
-0,08 |
b10 |
-0,21 |
0,0511 |
|
-0,2669117 |
0,710369056435279+3,4895754637212I |
0,710369 |
3,490 |
a11 |
0,04 |
b11 |
0,22 |
0,0495 |
|
-0,3485294 |
-0,34705882352939 -1,04705882352941i |
-0,34706 |
-1,047 |
a12 |
-0,02 |
b12 |
-0,07 |
0,0048 |
|
0,7698529 |
-2,2329138282402 +1,2706916705285i |
-2,23291 |
1,271 |
a13 |
-0,14 |
b13 |
0,08 |
0,0258 |
|
0,0882352 |
1,39644406072503+1,12572977822617i |
1,396444 |
1,126 |
a14 |
0,09 |
b14 |
0,07 |
0,0126 |
|
0,4066176 |
3,21792468335649-0,98546190721284I |
3,217925 |
-0,985 |
a15 |
0,20 |
b15 |
-0,06 |
0,0442 |
Столбец Действительная часть содержаться данные, полученные с помощью математической функции МНИМ.ВЕЩ., примененной к столбцу Y, а столбец Мнимая часть содержит значения, полученные с помощью математической функции МНИМ.ЧАСТЬ., примененной к столбцу Y.
Действительные и мнимые части связаны с гармоническими коэффициентами следующим образом:
![]() .
R2
=
.
R2
=
![]() .
ГрафикR2
представляет собой спектрограмму.
Посмотрев на график, можно выделить 3
основные гармоники (они соответствуют
3-м основным пикам).
.
ГрафикR2
представляет собой спектрограмму.
Посмотрев на график, можно выделить 3
основные гармоники (они соответствуют
3-м основным пикам).

Их и следует включить в модель.
Тогда для наших данных мы получим следующую модель: y = -0,3184 t + 17,888 + 0,4 cos t –0,12 sin t + 0,04 cos 5t + 0,44 sin 5t – 0,27 cos 8t + 0 sin 8t + 0,04 cos 11t – 0,44 sin 11t .
Проверить значимость гармоник можно, построив линейную регрессию остатков на эти 4 гармоники (8 переменных) и посмотрев значимость коэффициентов. Если хотя бы одна переменная из двух выбранных пар sin и cos значима, оставляем всю гармонику.
Таким образом, получаем гармоническую модель, описывающую наши данные. Сложив трендовую и гармоническую модели, получаем общую модель.
На рисунке представлены графики реальных и подогнанных значений (полученных по обобщенной модели) нашего ряда для остатков после удаления тренда. Причем на рисунке 2 графика подогнанных, оценочных значений – в первом случае мы просто взяли первые четыре гармоники, а для второго графика мы включили 5, 8 и 11 гармоники. Ниже в таблице приведены расчеты.
|
t |
u1 |
u2 |
u3 |
u4 |
y прогнозное 1 |
Остат ки |
u5 |
u8 |
u11 |
y прогноз ное 2 | ||||||||||||
|
0,000 |
0,40224 |
0,08727 |
-0,13956 |
-0,02169 |
0,328 |
0,03088 |
0,04439 |
-0,26544 |
0,04439 |
-0,17664 | ||||||||||||
|
0,393 |
0,32453 |
0,16120 |
0,09322 |
-0,1309 |
0,448 |
0,84926 |
0,38621 |
0,26544 |
0,38554 |
1,03719 | ||||||||||||
|
0,785 |
0,19747 |
0,14078 |
0,21101 |
0,02148 |
0,571 |
0,46764 |
-0,33928 |
-0,26544 |
-0,34104 |
-0,94576 | ||||||||||||
|
1,178 |
0,04037 |
0,03797 |
0,06850 |
0,13093 |
0,278 |
0,18602 |
-0,12716 |
0,26543 |
-0,12315 |
0,01513 | ||||||||||||
|
|
1,570 |
-0,1228 |
-0,0870 |
-0,158 |
-0,0212 |
-0,39 |
-0,2955 |
0,0445 |
-0,2654 |
0,4357 |
0,2149 |
| ||||||||||
|
|
1,963 |
-0,2674 |
-0,1611 |
-0,19 |
-0,1309 |
-0,75 |
-0,5772 |
-0,0578 |
0,2654 |
-0,2121 |
-0,0046 |
| ||||||||||
|
|
2,355 |
-0,3712 |
-0,1409 |
0,0128 |
0,0210 |
-0,478 |
-1,6588 |
-0,2790 |
-0,2654 |
-0,2725 |
-0,8170 |
| ||||||||||
|
|
2,748 |
-0,4187 |
-0,0382 |
0,1998 |
0,131 |
-0,126 |
1,2595 |
0,4190 |
0,2654 |
0,4218 |
1,1063 |
| ||||||||||
|
|
3,140 |
-0,4024 |
0,0868 |
0,1403 |
-0,0208 |
-0,196 |
-0,6220 |
-0,0409 |
-0,2654 |
-0,0520 |
-0,3583 |
| ||||||||||
|
|
3,533 |
-0,3249 |
0,1610 |
-0,0923 |
-0,1310 |
-0,387 |
-0,5036 |
-0,3878 |
0,2654 |
-0,3818 |
-0,5042 |
| ||||||||||
|
|
3,925 |
-0,1980 |
0,1410 |
-0,2110 |
0,0206 |
-0,247 |
0,2147 |
0,3370 |
-0,2654 |
0,3458 |
0,4174 |
| ||||||||||
|
|
4,318 |
-0,0410 |
0,0384 |
-0,0694 |
0,1310 |
0,059 |
-0,2669 |
0,1304 |
0,2654 |
0,1157 |
0,5116 |
| ||||||||||
|
|
4,710 |
0,1222 |
-0,086 |
0,1578 |
-0,0204 |
0,173 |
-0,3485 |
-0,436 |
-0,2653 |
-0,4348 |
-1,1369 |
| ||||||||||
|
|
5,103 |
0,2668 |
-0,1610 |
0,1904 |
-0,131 |
0,165 |
0,7698 |
0,2029 |
0,2653 |
0,2188 |
0,6871 |
| ||||||||||
|
|
5,495 |
0,3709 |
-0,141 |
-0,0118 |
0,0202 |
0,238 |
0,0882 |
0,2817 |
-0,2653 |
0,2664 |
0,2828 |
| ||||||||||
|
|
5,888 |
0,4186 |
-0,0387 |
-0,1995 |
0,1311 |
0,311 |
0,4066 |
-0,4180 |
0,2653 |
-0,4238 |
-0,5765 |
| ||||||||||
Где
![]()
u1=![]()
u2=![]() …,
…,
u11=![]() .
.
{y прогнозное 1} = a0 + u1 +u2 +u3 +u4
{y прогнозное 2} = a0 + u5 +u8 +u11.
Мы подбираем гармоническую модель для остатков. Потом, выбрав из двух моделей одну, наиболее точную, мы складываем ее с трендовой моделью, и получаем обобщенную модель.
График ее выглядит следующим образом:
Из анализа графика можно увидеть, что получившаяся модель достаточно хорошо описывает данные, достаточно точная.
