Решение

1)

-уравнение регрессии.

=2000-40(90/40)²=1797,5

220,9-19,1+67,3-05+202,5=66,6

ЕSS=1797,5-66,6=1797,5-66,6=1730,9

Очень маленькое значение, объем продаж лишь на 3,7% объясняется температурой. Значит, сумма средств, потраченных на лекарство, слабо зависит от температуры.

2)

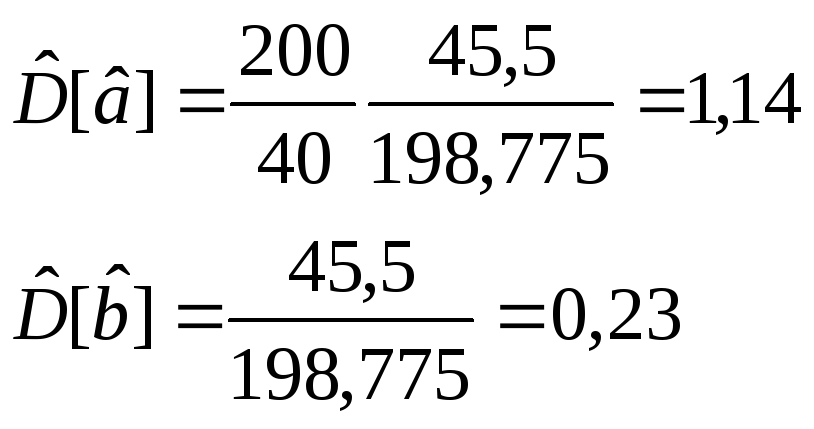
Задача 3. По совокупности 30 предприятий торговли изучается зависимость между признаками: – цена за товар А, тыс. руб.;– прибыль торгового предприятия, млн. руб. При оценке линейной регрессионной модели были получены следующие промежуточные результаты.

Поясните, какой показатель корреляции можно определить по этим данным.

Для вычислений будем использовать следующие формулы:

- общая сумма квадратов отклонений, TSS;

- сумма квадратов отклонений, обусловленная регрессией, RSS;

- остаточная сумма квадратов отклонений, ESS.

Решение. По указанным данным можно определить индекс корреляции для нелинейной регрессии:

Так же можно найти R²:

= 1-=0,675

Не очень большой R² свидетельствует о не очень сильной линейной связи. В то же время был подсчитан коэффициент не линейной связи (0,822), который свидетельствует о достаточно существенной зависимости.

Задача 4: Нахождение параметров регрессии на примере линейной функции.

По семи территориям Уральского региона за 2002 год известны значения двух признаков:

• - расходы на покупку продовольственных товаров в общих расходах, %;

• - среднедневная заработная плата одного работающего, руб.

Номер	Регион
1	Удмуртская респ.	68,8	45,1
2	Свердловская обл.	61,2	59
3	Башкортостан	59,9	57,2
4	Челябинская обл.	56,7	61,8
5	Пермская обл.	55	58,8
6	Курганская обл.	54,3	47,2
7	Оренбургская обл.	49,3	55,2

Задание.

1. Для характеристики зависимости от рассчитать параметры следующих функций: 1.1) линейной; 1.2) степенной;

2. Оценить каждую модель через коэффициент детерминации R². Решение.

1. Линейная регрессия = а + b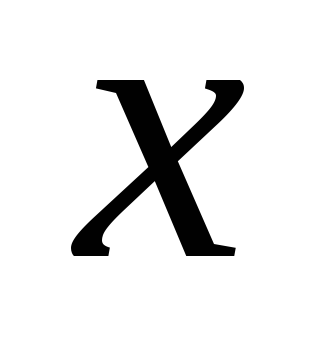

Для определения параметров а и b линейной регрессии по исходным данным рассчитываем

следующие величины:

Результаты промежуточных вычислений приведены в таблице.

таблица 2.1.

							-
1	68,8	45,1	3102,88	2034,01	4733,44	61,33	7,5
2	61,2	59	3610,8	3481	3745,44	56,54	4,7
3	59,9	57,2	3426,28	3271,84	3588,01	57,16	2,8
4	56,7	61,8	3504,06	3819,24	3214,89	55,57	1,2
5	55	58,8	3234	3457,44	3025	56,61	-1,5
6	54,3	47,2	2562,96	2227,84	2948,49	60,61	-6,2
7	49,3	55,2	2721,36	3047,04	2430,49	57,85	-8,5
Итого	405,2	384,3	22162,3	21338,4	23685,8	-55,58	0,0
Среднее значение	57,88	54,9	3166,05	3048,34	3383,68
Σ	5,74	5,86
σ2	32,92	34,34

Уравнение регрессии: = 76,88-0,35.

С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ых пункта. Для определения направления и тесноты связи рассчитаем линейный коэффициент парной корреляции:

Связь умеренная, обратная.

Определим коэффициент детерминации:

• можно рассчитать по формуле R² = (-0,357)² = 0,127.

• получить в рамках оценивания параметров регрессии на компьютере.

Вариация результата на 12,7 % объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения , определим теоретические (расчётные) значения.

2. Степенная функция.

Проведём процедуру линеаризации путём логарифмирования обеих частей уравнения: lg = lga + b * lg

После переобозначения мы будем оценивать регрессию вида: = с + d

							-	(-)2
1	1,8376	1,6542	3,0397	2,7363	3,3767	61,0	7,8	61,29
2	1,7868	1,7709	3,1641	3,1359	3,1925	56,3	4,9	24,21
3	1,7774	1,7574	3,1236	3,0884	3,1592	56,8	3,1	9,60
4	1,7536	1,7910	3,1406	3,2076	3,0751	55,5	1,2	1,42
5	1,7404	1,7694	3,0794	3,1307	3,0289	56,3	-1,3	1,79
6	1,7348	1,6739	2,9040	2,8021	3,0095	60,1	-5,8	34,22
7	1,6928	1,7419	2,9488	3,0344	2,8657	57,4	-8,1	65,73
Итого	12,3234	12,1587	21,4002	21,1354	21,7076	403,5	1,7	198,26
Среднее значение	1,7626	1,7396	3,0572	3,0193	3,1011			28,27
Σ	0,0425	0,0484
σ2	0,0018	0,0012

Рассчитаем С (или lg a) и b:

Получим линейное уравнение: Y= 2,278 – 0,298 X

Выполнив его потенцирование, получим:

= 10^2,278*^-0,298 = 189,7^-0,298

Подставляя в данное уравнение фактические значения , получаем теоретические значения результата .

Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.

Определение: Доверительный интервал – это интервал, накрывающий истинное значение (которое мы не знаем, но строим его оценку, т.е. приблизительное значение) параметра с заданной вероятностью α.

Задача 5. Построить доверительный интервал для истинных значений регрессии при всех наблюдениях( i =1:14).

Решение: Доверительный интервал для одного истинного значения регрессии при заданном уровне значимости будет следующим:

- , где -квантиль распределения Стьюдента приf степенях свободы и заданном уровне значимости α. - дисперсия оценки истинного значения. Она рассчитывается следующим образом:.

Пусть известно, что T=14, 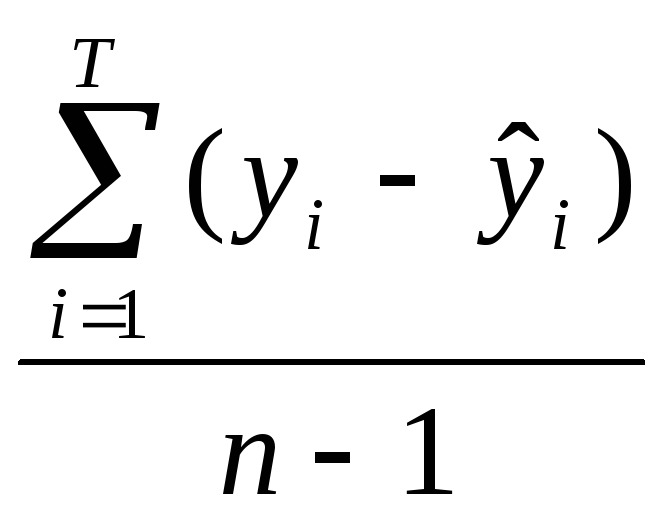=2,0809,Находим квантиль распределения Стьюдентапри α=0,05 иf = 14-1-1=12 степенях свободы. Для этого в Excel в ячейку надо ввести строчку: {==СТЬЮДРАСПОБР(0,05;12)}и нажать Ввод. Он равен 2,179. Пусть с помощью МНК найдены оценки коэффициентов регрессии =7,0356 + 0,5435.

Представим расчеты в таблице. Значенияинам даны. Остальные столбцы рассчитываются.

№							-
1	20	32	24,4276	388,4841	0,9692	2,1119	22,3157	26,53
2	24	30	23,3406	471,3241	1,0360	2,2575	21,0831	25,59
3	28	36	26,6016	246,8041	0,8428	1,8364	24,7652	28,13
4	30	40	28,7756	137,1241	0,7299	1,5905	27,1850	30,36
5	31	41	29,3186	114,7041	0,7047	1,5356	27,7830	30,85
6	33	47	32,5806	22,1841	0,5890	1,2835	31,2971	32,86
7	34	56	37,4716	5,2441	0,5838	1,722	26,1994	38,74
8	37	54	36,3846	18,4041	0,5653	1,2318	35,1252	37,61
9	38	60	39,6456	68,7241	0,6498	1,4159	38,2297	41,06
10	40	55	36,9276	10,8241	0,5732	1,2491	35,6785	38,17
11	41	61	40,1896	86,3041	0,6713	1,4628	38,7268	41,65
12	43	67	43,4496	233,7841	0,8302	1,8089	41,6407	45,25
13	45	69	44,5376	298,9441	0,8914	1,9424	42,5952	46,48

В столбцах 8 и 9 (предпоследний и последний) указаны соответственно нижние и верхние доверительные границы. Например, при =32 истинное значение регрессии генеральной совокупности с доверительной вероятностью 0,95 будет находиться в интервале 22,3157≤≤26,53

Доверительные интервалы для параметров линейной регрессии вычисляются по формуле:

, где - оценка стандартного отклонения.А- это оценка параметра регрессии, т.е. либоа , либо b. Определим доверительные границы для параметров регрессии генеральной совокупности. Точечные оценки параметров: а=7,0356 , b = 0,5435. Стандартные ошибки оценок параметров регрессии = 2,1532, а=2,179 . Зададимся уровнем значимости α=0,05.. В соответствии с выше приведенной формулой получаем следующие доверительные границы для:а:7,0356 ±2,179 * 2,132 , или, 7,0356 ±4,6918.

b: 0,5435±0,0876.

Задачи для самоконтроля.

Задача 6. n = 52;

Построить и оценить модель линейной регрессии: = а + b. Для этого найти:

1) â -? - ? TSS-? ESS-? R²-? Y(-3)-?

Задача 7. Известно, что:

	2	4	-3	2	5	-6	2	4	7
	3	2	-1	3	0	-4	2	5	6

Построить регрессию на , т.е. оценить коэффициенты регрессии

=+.

Найти:; TSS, ESS, RSS, R²,

Задача 8. Пусть Х₁, Х₂, …Х_n – независимые, одинаково распределенные случайные величины.

Приведено 4 оценки для математического ожидания x_i:

1. y₁=x₁

2. y₂=0,2*x₁+0,8*x₂

3. y₃=x₁+x₂-x₃

4. y₄=½x₁+⅓x₂+¼x₃

E[x_i]=μ ; Var[x_i]=V[x_i]

Какие из указанных оценок являются несмещенными?

Какая оценка среди несмещенных является наиболее эффективной?

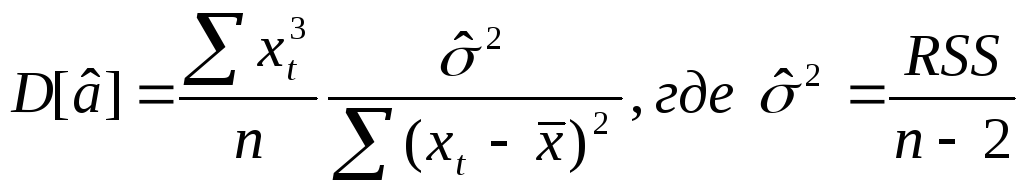Примечание: Несмещенной называется оценка, математическое ожидание которой равно истинному значению, то есть . Эффективной называется оценка, обладающая наименьшей дисперсией. Дисперсия а рассчитывается по формуле:,a