Понятие метрики графа

Метрика графа основана на понятии расстояния. Назовем расстоянием d(x_i, x_j) = d_ij между вершинами x_i,x_jX графа G=(X, U) длину кратчайшей цепи, соединяющей эти вершины. Под длиной цепи понимается число входящих в нее ребер.

Функция d(x_i, x_j), определенная на множестве ребер графа G, называется метрикой графа. Метрика удовлетворяет аксиомам Фреше:

 x_i x_j  X[d(x_i, x_j)  0];

 x_i x_j  X[d(x_i, x_j) = 0  x_i = x_j];

 x_i x_j  X[d(x_i, x_j) = d(x_i, x_j)];

 x_i ,x_j ,x_k  X[d(x_i, x_j) + d(xj, x_k)  d(x_i, x_k)]

т.к. d(x_i, x_j) кратчайшая цепь

Функция расстояний задается матрицей

0, еслиx_i = x_j;

D = || d_ij|| =

d_ij, если x_i  x_j;

	1	2	3	4	5
1	0	3	1	3	2
2	3	0	2	1	1
3	1	2	0	2	1
4	3	1	2	0	1
5	2	1	1	1	0

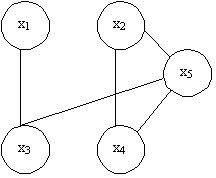
D =

Рисунок 7.24

Список расстояний можно задать в виде множества кортежей длины три < x_i ,x_j ,d_ij >.

Для графа, приведенного на рисунке 7.24.

D={<1,2,3>, <1,3,1>, <1,4,3>, <1,5,2>, <2,3,2>, <2,4,1>, <2,5,1>, <3,4,2>, <3,5,1>, <4,5,1>}

Диаметр графа d(G) определяется как максимальное расстояние между его вершинами.

D(G) = max dij, x_i x_j  X

Интерес представляет нахождение расстояний в графах частного вида, называемых координатной решеткой.

G_r = (X_r, U_r)

В графе G_r = (X_r, U_r) множество X_r соответствует узлам решетки, а U_r - вертикальным и горизонтальным отрезкам, соединяющим узлы решетки.

Введем декартову систему координат с осями s и t.

t

x₁ x₂ x₃ x₄ x₅ x₆ s

Рисунок 25

Расстояние между соседними узлами решетки называют шагом решетки и принимают равным единице. Расстояние между двумя произвольными вершинами в решетке G_r рассчитывается:

d_ij = |s_i – s_j| + |t_i – t_j| ,

где s_i, s_j и t_i, t_j - координаты x_i и x_j .

Обычно задаются размеры решетки p x q, где p – число узлов решетки по оси s, q – not. Например, d(7, 13) = |1 – 2| + |5 – 0| = 6.

Граф G_r удовлетворяет аксиомам Фреше. Если произвольный граф G отображается в G_r так, что любые вершины G размещаются в узлах решетки, то расстояние между вершинами G определяется как расстояние между соответствующими узлами решетки G_r.

Любой граф G может быть отображен в решетку G_r.

Для подсчета суммарной длины L(G) ребер графа G, отображенного в решетку G_r, введем понятие матрицы геометрии D_.

D_ представляет собой часть матрицы расстояний D, в которой исключены элементы d_ij, если вершины x_i x_j  X не смежны в графе G.

0, если r_ij = 0;

d^_ij =

d_ij, если r_ij  0.

Сумма элементов матрицы D_ определяет удвоенную суммарную длину L(G) ребер графа G при данном его отображении в решетку G_r.

Цикломатическое число, раскраска

Наименьшее число ребер, которое необходимо удалить из графа G, чтобы он стал ациклическим, называется цикломатическим числом графа. Для графа G=(X, U), |X| = n, |U| = m цикломатическое число j(G) = m – n + k, где m – число ребер графа, n – число вершин, k – число компонент связности графа. Для графа, состоящего из одной компоненты связности j(G) = m – n + 1; например, на рис.26 j(G) = 7 – 5 = 2; т.е. после удаления двух ребер граф становится ациклическим, в примере это ребра, (например, (х₄, х₂), (х₄, х₃)). Чтобы узнать, какие ребра удалять, необходимо каждый раз удалять ребро, которое разрушает хотя бы один цикл.

Рисунок 7.26

Раскраской вершин графа называется разбиение множества вершин графа на l непересекающихся классов (подмножеств)

таких, что внутри каждого подмножества Х_i не должно быть смежных вершин.

Если каждому подмножеству Х_i поставить в соответствие определенный цвет, то вершины внутри подмножества можно окрасить в один цвет, вершины другого – в другой и т.д. до полной раскраски. В этом случае граф называется l-раскрашиваемым. Наименьшее число подмножеств, на которое разбивается граф при раскраске, называется хроматическим числом K(G).

Очевидно, полный граф K_n можно раскрасить только в n цветов K(Kn)=n.

Для связного графа G = (X, U) с n-1  m  n(n-1)/2 верхняя оценка хроматического числа:

Нижней оценкой K(G) является число вершин в наибольшем полном подграфе графа G.

Хроматическое число обычно определяется с помощью методов линейного программирования.

Важное практическое применение имеют 2-раскрашиваемые или двудольные (граф Кёнига) (бихроматические) графы. Обозначается двудольный граф G_n1,n2 =(X₁, X₂, U), где X₁X₂=X, X₁X₂=, а ребра соединяют только подмножества X₁ и X₂ между собой.

Пример двудольного графа.

G_n1,n2 =(X₁, X₂, U); |X₁| = n₁ = 4;

|X₂| = n₂ = 3; X₁ = {x₁, x₂, x₃, x₄};

X₂ = {x₅, x₆, x₇}.

Рисунок 7.27. Двудольный граф

Граф K_{n1, n2} называется полным двудольным графом, если любая вершина x_iX₁ смежна каждой вершине x_jX₂ (ij).

В двудольном графе множество X₁ можно раскрасить одним цветом, Х₂ – другим цветом.

Рисунок 7.28. Полный двудольный граф К₃₂.

При разработке алгоритмов компоновки, размещения и трассировки возникает необходимость определения двудольности некоторого графа или выделения в этом графе максимальных непересекающихся двудольных частей.

Теорема 4. Граф G_{n1, n2} является двудольным тогда, и только тогда, когда он не имеет простых циклов нечетной длины.

Рассмотрим число внутренней устойчивости. Если любые вершины в графе G = (X, U) X’X, не смежны, то это подмножество называется внутренне устойчивым.

Тождественные преобразования графов, сводимые только к переобозначению вершин и ребер, приводят к получению изоморфных графов.