6. Булевы функции

Двоичная функция двоичного аргумента называется булевой функцией.

y= f(x₁, x₂,…, x_n), x_i {0,1}, y {0,1}, i = 1,n.

Система булевых функций задается следующим образом:

Будем говорить, что две функции равны, если их значения совпадают на любой комбинации значений переменных.

f(x₁,…, x_n) = g (x₁,…, x_n)

Различными считаются функции не совпадающие хотя бы на одной комбинации переменных.

Число различных функций равно ,

Пусть n = 0, тогда = 2, т.е. функция принимает значение 0 или 1.

При n=1 число различных функций равно 4.

х	функция
	нуль	тождественна	отрицательна	единица
0	0	0	1	1
1	0	1	0	1
	0	х	х', ¬x	1

При n=2, число различных функций равно 16.

Функции
х1	x2	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15	f16
0 0 1 1	0 1 0 1	0 0 0 0	0 0 0 1	0 0 1 0	0 0 1 1	0 1 0 0	0 1 0 1	0 1 1 0	0 1 1 1	1 0 0 0	1 0 0 1	1 0 1 0	1 0 1 1	1 1 0 0	1 1 0 1	1 1 1 0	1 1 1 1

Приведем эти булевы функции.

f₁(x₁, x₂) = 0 – константа 0;

f₂(x₁, x₂) = x₁  x₂ – конъюнкция;

f₃(x₁, x₂) = x₁  =

= x₁  x₂ – левая коимпликация (читается «не если x₁, то x₂»);

f₄(x₁, x₂) =   x₁  x₂ = x₁;

f₅(x₁, x₂) =  x₂ = x₁ x₂= =

правая коимпликация;

f₆(x₁, x₂) =  x₂  x₁  x₂ = x₂;

f₇(x₁, x₂) =  x₂  x₁  = x₁  x₂ – сложение по модулю два, дизъюнкция с исключением;

f₈(x₁, x₂) = x₁  x₂ – дизъюнкция;

f₉(x₁, x₂) =  = = x₁○ x₂ – функция Вебба;

f₁₀(x₁, x₂) =  = x₁~ x₂ – функция эквивалентности;

f₁₁(x₁, x₂) = - отрицание;

f₁₂(x₁, x₂) =   x₁   x₁  x₂ =  x₁ = x₁← x₂ – правая импликация (читается «если x₂, то x₁»);

f₁₃(x₁, x₂) = - отрицание;

f₁₄(x₁, x₂) =    x₂  x₁  x₂ =  x₂ = x₁  x₂ – левая импликация (читается «если x₁, то x₂»);

f₁₅(x₁, x₂) =    x₁  =  = x₁| x₂ – функция Шеффера;

f₁₆(x₁, x₂) = 1 –константа 1.

Способы задания булевой функции

1. Табличный способ

Область определения булевой функции – совокупность всевозможных наборов переменных, состоящих из нулей и единиц. Поэтому для задания булевой функции достаточно задать значение функции на всех наборах переменных.

Естественным расположением наборов является расположение в порядке возрастания десятичного числа соответствующего данному набору.

№ набора	х1	х2	х3	f(х1, х2 , х3)
1 2 3 4 5 6 7 8	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 1 0 1 0 1

2. Представление вершинами n-мерного куба.

Множество значений вектора x=(x₁, x₂,…, x_n) составляет булево пространство. Каждому значению вектора сопоставлен элемент пространства. Число компонент вектора определяет размерность пространства.

n = 0 ●

x₁

n= 1

n = 2

n= 3

Расстояние между вершинами n-мерного куба есть число компонент, значениями которых эти вершины отличаются. Также расстояние называется расстоянием по Хемингу. Соседние вершины n-мерного куба различаются одной компонентой.

3. Задание булевой функции формулами.

Пусть F = {f₁, f₂, …, f_n} – множество булевых функций. Формулой над F называется выражение вида F[F] =  (t₁,…, t_n), где F и t_i, либо переменная, либо формула над F. Множество F называется базисом, функция  называется главной (внешней) операцией (функцией), a t_i называются подформулами.

Систему функций будем называть функционально полной, если любая булева функция может быть представлена в виде суперпозиции функций этой системы. Функционально полная система называется базисом. Базис называется безизбыточным, если ни одну из функций базиса нельзя исключить так, чтобы оставшаяся система функций была функционально полной. Базис называется минимальным, если он содержит наименьшее из возможных число функций.

Существует 17 базисов, в каждом из которых нельзя вычеркнуть ни одну функцию без потери полноты.

Базис Вебба – { 0 };

Базис Шеффера – { | };

{, ~ };

Импликативный базис - {, 0};

{, };

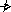{, -} – коимпликативный базис;

{, };

{, ˉ} – импликативный базис;

{&, ˉ} – конъюнктивный базис Буля;

{, ˉ} – дизъюнктивный базис Буля;

{, 1} – коимпликативный базис;

{~, &, 0};

{~, , 0};

{, &, ~};

{, , ~};

{, &, 1} – базис Жегалкина;

{, , 1}.

Техническая реализация базисных функций может быть основана на использовании различных физических явлений, например, импликация и коимпликация может быть основана на использовании магнитных явлений, а функции Шеффера и Вебба – на использовании явлений в полупроводниках.