Операции над отношениями

Для бинарных отношений обычным образом определены теоретико-множественные операции объединения, пересечения и др.

Пусть R₁  А х С отношение из А в С, а R₂  С х В – отношение из С в В.

Композицией двух отношений R₁ и R₂ называется отношение R  А х В из А в В, определяемое следующим образом:

R = R₁○R₂ = {<a,b>| cуществует С такое, что <a,c>  R₁ и <c,b>  R₂}

Обратным отношением для R называется отношение

R¹ = {<a,b>| <b,a>R}

Для любых бинарных отношений выполняются свойства:

Свойство 1:

(R^-1)^-1 = R

Cвойство 2: Пусть S, R – отношения, тогда

(S, R)^-1 = R^-1○ S^-1

Свойство 3: Если R  S и T  Y, то

T R  Y S

Функция f : A→B может быть определена как отношение, определенное на множестве А х В, обладающее свойством:

Если (a,b)  f и (a,c)  f, то b = c.

Область определения функции обозначается как D_f, а область ее значений как R_f.

Если D_f =А и R_f В, то говорят, что функция f задана на множестве А со значениями во множестве В и осуществляет отображение множества А во множество В. Вместо <a,b>  f , пишут b = f(a), здесь b - значение функции, соответствующее аргументу а.

Пусть f : A→B. Функция называется инъективной, если для любых а₁, а₂, b из b=f(a₁) и b=f(a₂) следует, что a₁=a₂ (рисунок 2.6).

Функция f называется сюръективной, если для любого элемента bB существует элемент аА такой, что b=f(а) (рисунок.2.7).

Функция f называется биективной, если f одновременно сюръективна и инъективна (рисунок 2.8).

Если существует биективная функцияf : А →В, то говорят, что f осуществляет взаимнооднозначное соответствие между множествами А и В.

Рисунок.2.5 - Отношение, но не функция

Рисунок 2.6 - Инъективная функция

Рисунок 2.7 - Сюръективная функция

Рисунок 2.8 - Биективная функция

Свойства бинарных отношений

Рассмотрим наиболее важные свойства бинарных отношений. Пусть задано множество А, А х А=А² и отношение R на нем.

Отношение R в множестве А называется рефлексивным, если для каждого элемента аА справедливо утверждение a R a. Если изображать рефлексивность графически, то элемент имеет петлю.

Рисунок 2.9 - Рефлексивное отношение

Отношение R в множестве А называется симметричным, если для любых а,bA выполнено: aRb следует bRa; или (a,b)  R  (b,a)R a b.

Графически симметричность можно изобразить следующим образом:

Рисунок 2.10 – Симметричное отношение

Отношение R называется транзитивным, если для любых a,b,cА, выполняется: a R b и b R c  a R c, при этом a  b, b  c, a  с. Граф, представляющий транзитивное отношение R, выглядит следующим образом:

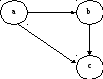
Рисунок 2.11 – Транзитивное отношение

При этом дуга (а,с) называется транзитивно замыкающей дугой.

Бинарное отношение R в множестве А, обладающее свойствами:

рефлексивности: для каждого aA, (a,а) R

транзитивности: для любых a,b,сA следует (a,b)R, (b,с)R (a,с)R.

Называется отношением упорядоченности и обозначается . .

Если любые два элемента а, b упорядоченного множества находятся в отношении упорядоченности ab или ba, то это множество называется линейноупорядоченным, в противном случае – частично упорядоченным.

Например, отношение a  b на множестве действительных чисел является отношением упорядоченности. Во множестве подмножеств некоторого универсального множества U отношение АВ также есть отношение упорядоченности. Схема организации подчинения в учреждении есть отношение частичного порядка на множестве должностей.

Бинарное отношение в множестве А, обладающее свойствами антирефлексивности, антисимметричности и транзитивности, называется отношением строгой упорядоченности и обозначается <.

Рассмотрим отношение включения . Это отношение рефлексивно: A_i  A_i (множество A_i включает само себя). Если A_i  A_j и A_j  A_i, то A _i= A_j, следовательно отношение антисимметрично, если A_i  A_j и A_jA_k, то A_i  A_k, то есть отношение  транзитивно и является отношением упорядоченности . Множество А с заданным на нем отношением упорядоченности  называется упорядоченным этим отношением. Отношение включение является частично упорядоченным множеством.

Частично упорядоченное множество изображают в виде графовG = (X, U). Например, пусть А = {1, 2, 3}. Рассмотрим отношение быть подмножеством. Получаем следующую диаграмму (удалены петли и транзитивно замыкающие дуги), называемую диаграммой Хассе Н.

Рисунок 2.12 – Пример диаграммы Хассе.

Понятие непосредственного старшего легко задается в частично упорядоченном множестве следующим определением: a_i покрывает a_j. Это означает, что a_j < a_i и не найдется такого элемента а_k, что a_j < a_k < a_i. Если рассмотрим подмножество A’  A, и найдем такой элемент a_LA, что a_i < a_L для любого элемента a_iA’, то этот элемент называется мажорантой подмножества A’. Аналогично, если найдется элемент a_A, такой, что a_ < a_j для любого элемента a_j  A’, то элемент a_ называется минорантой подмножества A’.

Если отношение R, определенное на множестве А, является рефлексивным, симметричным и транзитивным, то его называют отношением эквивалентности.

Классом эквивалентности, порожденным элементом х, называется подмножество множества Х, состоящее из тех элементов у  Х, для которых х R y. Класс эквивалентности, порожденный через х, обозначается [x].

Например, дано множество A = {0, 1, 2, 3}. Определим отношение R, отвечающее общепринятому понятию «равно». E = {<0, 0>, <1,1>, <2,2>, <3,3>}. Для заданного отношения эквивалентности Е существуют четыре класса эквивалентности [0] = {0}, [1] = {1}, [2] = {2}, [3] = {3}.

Отношение принадлежности к одной студенческой группе на множестве студентов института – это отношение эквивалентности, и классом эквивалентности является множество студентов одной группы.

Необходимо заметить, что класс эквивалентности порождается любым своим элементом. Классы эквивалентности, соответствующие отношению эквивалентности R определенному на множестве А, разбивают множество А на конечное число непустых непересекающихся множеств.

Например, определим отношение R на множестве натуральных чисел следующим образом:

а R b справедливо, если и только если |a – b| делится на 5 без остатка. В этом случае множество N разбивается на пять бесконечных классов эквивалентности:

{{1,6,11,…}, {2,7,12,…}, {3,8,13,…}, {4,9,14,…}, {5,10,15}}.

Если R – произвольное отношение, определенное на множестве А, то его рефлексивным замыканием называется наименьшее рефлексивное отношение, определенное на множестве А, для которого отношение R является подмножеством.

Например, если R = {<0,1>, <1,1>, <1,2>} – отношение, определенное на множестве A = {0,1,2}, то его рефлексивным замыканием является множество {<0,0>, <0,1>, <1,1>, <1,2>, <2,2>}.

Рисунок 2.13 – Рефлексивное замыкание

Симметричным замыканием является множество {<0,1>, <1,0>, <1,1>, <1,2>, <2,1>}.

Рисунок 2.14 - Транзитивное замыкание {<0,1>, <0,2>, <1,1>, <1,2>}.

Рисунок 2.15 – Симметричное замыкание

Заметим, что рефлексивным замыканием отношения <, определенного на множестве целых чисел, является отношение , его симметричным замыканием является отношение , а транзитивным замыканием является само отношение <.