Изоморфизм графов

Два графа G=(X, U) и G’=(X’, U’) называют изоморфными, если можно установить взаимно-однозначное соответствие XX’ , UU’ такое, что если (x_i, x_j) X  (x_i, x_j) X’ , то ребро u = (x_i, x_j)U  u’ = (x’_i, x’_j) U’. Изоморфизм есть отношение эквивалентности на графах. Изоморфные графы могут быть получены один из другого при помощи перенумерации их вершин. Если изоморфные преобразования проводятся с графом, заданным матрицей смежности, то они сводятся к перестановке местами соответствующих строк и столбцов.

а б

в

Рисунок 29. Граф G и изоморфные ему

В общем случае для определения изоморфизма необходимо сделать n! сравнений.

При покрытии функциональной схемы набором стандартных модулей или при решении задачи типизации необходимо устанавливать изоморфизм между графом G и какой-либо частью другого графа G’.

При конструировании схем к их топологическому чертежу предъявляются требования получения плоского изображения схем.

Граф G=(X, U) называется плоским, если он расположен на плоскости таким образом, что ребра имеют общие точки лишь в вершинах. Граф, изоморфный плоскому расположенный на плоскости и имеющий пересечения ребер, называется планарным.

Область плоскости, ограниченная ребрами плоского графа внутри которой нет ни вершин, ни ребер, называется гранью.

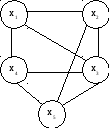
а б

Рисунок 30. Планарный граф (а) и изоморфный ему плоский граф (б)

Ребра грани образуют простой цикл. Плоский граф имеет всегда одну бесконечную грань, не ограниченную ребрами. Существует формула Эйлера, позволяющая установить связь между числом вершин и числом ребер плоского графа:

n – m + f = 2 , где f – число граней плоского графа.

Определить планарность можно с помощью различных критериев.

Пусть задан граф G=(X, U). Подразбиением ребра u_k = (x_i, x_j) называют замену его двумя ребрами u_р1 = (x_i, x_р) и u_р2 = (x_р, x_j) с введением новой вершины x_р . Два графа называют гомеоморфными, если они обладают изоморфными подразбиениями.

Теорема (Понтрягина-Куратовского). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных полному графу К₅ и полному двудольному графу К_3,3.

Граф планарен тогда и только тогда, когда планарны все его связные компоненты.

Распространенная методика определения планарности заключается в нахождении в графе G максимального цикла С, лучше Гамильтонова и размещение его на плоскости в виде замкнутой самопересекающейся кривой. Далее в оставшейся части определяют пересекающиеся по ребрам пути и предпринимают попытки разместить каждый из путей либо внутри С, либо полностью вне С. если таким образом размещается весь граф, следовательно, он планарен, в противном случае – не планарен.

Заметим, что если граф связный и плоский, то и двойственный ему граф G_s также будет плоским и связным.