
А.В.Шатина МО 2012 версия 20.09.2013
.pdf
71
базис
a |
1 |
|
|
a |
3 |
|
|
a |
2 |
|
|
z |
|
|
|
c
0
0
0
b x |
|
b |
|
2 |
|
3 2 |
|
1 2 |
|
0 |
|
0
a |
1 |
|
|
1 |
|
0 |
|
0
0
0
0
a |
2 |
|
|
0 |
|
0 |
|
1
0
0
0
a |
3 |
|
|
0 |
|
1 |
|
0
0
0
0
a |
4 |
|
|
1 |
|
1 2 |
|
1 2 |
|
0
0
0
a |
5 |
|
|
0 |
|
1 2 |
|
1 2 |
|
0
0
-1
a |
6 |
|
|
1 |
|
0 |
|
0
0
1
-1
a |
7 |
|
|
1 |
|
1 2 |
|
1 2 |
|
0
1
-1
a |
8 |
|
|
0 |
|
1 2 |
|
1 2 |
|
0
1
t
Так как 0 , то точка 2;1 2;3 2;0;0;0;0;0 |
является реше- |
нием вспомогательной задачи, а точка 2;1 2;3 |
2;0;0 является |
начальной крайней точкой исходной задачи. Используя получен-
ные разложения векторов по базису |
1 |
, a |
3 |
, a |
2 |
, строим симплекс- |
a |
|
|
ную таблицу исходной задачи:
базис
a |
1 |
|
|
a |
3 |
|
|
a |
2 |
|
|
z |
|
|
|
c
3
2
-2
b x |
|
b |
|
2 |
|
3 2 |
|
|
|
1 2 |
|
8 |
|
3
a |
1 |
|
1
0
0 |
3 |
0 |
-2 |
2 |
-2 |
1 |
t |
||||
a |
2 |
a |
3 |
a |
4 |
a |
5 |
|
|
|
|
|
|
||||
0 |
0 |
1 |
0 |
|
||||
0 |
1 |
1 2 |
1 2 |
3 |
||||
1 |
0 |
1 2 |
1 2 |
1 |
||||
-2 |
2 |
5 |
0 |
|
||||
0 |
0 |
7 |
-1 |
|
||||
Последняя строка содержит один отрицательный элемент,
соответствующий вектору |
a |
5 |
. Вычисляем элементы последнего |
|
столбца и выбираем наименьший положительный, соответству-
ющий разрешающей строке |
a |
2 |
. |
Для нового |
базиса |
1 |
, a |
3 |
, a |
5 |
||||||||||
|
a |
|
|
|||||||||||||||||
строим таблицу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
3 |
|
|
-2 |
|
2 |
-2 |
1 |
|
t |
|
|
|
|
|
|
|
базис |
|
b xb |
a1 |
|
|
a 2 |
|
a3 |
a 4 |
a5 |
|
|
|
|
|
|
|
||
|
a |
1 |
3 |
2 |
1 |
|
|
|
0 |
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
3 |
2 |
1 |
0 |
|
|
-1 |
|
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
5 |
1 |
1 |
0 |
|
|
|
2 |
|
0 |
-1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
9 |
3 |
|
|
|
0 |
|
2 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
0 |
6 |
0 |
|
|
|
|
|
|
|
|
72
Так как
Smax 9 .
0
, то
xˆ 2;0;1;0;1
является решением задачи,
Замечание. В данной задаче можно было ограничиться введением одной искусственной переменной x6 , так как два послед-
них столбца матрицы A задачи являются столбцами единичной
матрицы. Тогда число шагов значительно бы уменьшилось. |
● |
Пример 4. Решить задачу линейного программирования: |
|
f x 2x1 x2 x3 x5 min ; |
(з) |
2x2 x4 x5 3, |
|
x3 2x4 2, |
|
x1 3x2 x4 5, |
|
x1 x2 3, x j 0, j 1,...,5. |
|
На первом шаге приведем данную задачу форме, введя дополнительные переменные x6 , x
к канонической 7 . Получим сле-
дующую задачу:
f x
x |
|
3 |
|
2x x |
2 |
x |
x |
max |
1 |
3 |
5 |
|
|
x1 3x2 x4 x6 5, |
||||
x1 x2 x7 3, |
|
|||
2x2 x4 x5 3, |
|
|||
2x4 2, |
x j 0, j 1, ... ,7 . |
|||
;
(з1)
Полученную задачу линейного программирования (з1) в канонической форме будем решать методом искусственного базиса. Для этого рассмотрим вспомогательную задачу, добавляя искусственные переменные x8 , x9 :
x8 x9 max ; (з2) x1 3x2 x4 x6 5,
x1 x2 x7 3,
2x2 x4 x5 x8 3,

73
x3 2x4 x9 2 |
, |
x j 0, |
j |
Начальная крайняя точка задачи (з2)
1, x
... ,9 . |
|
0 |
0,0,0,0,0,5,3,3,2 |
|
|
.
Базисные векторы
a |
6 |
1,0,0,0 , a |
7 |
|
|
0,1,0,0 , a |
8 |
0,0,1,0 , a |
9 |
|
|
0,0,0,1
.
Составим симплексную таблицу для задачи (з2):
базис
a6
a |
7 |
|
|
a |
8 |
|
|
a |
9 |
|
|
z |
|
|
|
c
0
0
-1
-1
b x |
b |
|
|
|
5
3
3
2
-5
0 |
0 |
0 |
0 |
a1 |
a 2 |
a3 |
a 4 |
1 |
3 |
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
2 |
0 |
-1 |
0 |
0 |
1 |
-2 |
0 |
-2 |
-1 |
3 |
0 |
-2 |
-1 |
3 |
0 0
a |
5 |
a |
6 |
|
|
0 1
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
1 0
0 |
-1 |
-1 |
|||
a |
7 |
a |
8 |
a |
9 |
|
|
|
|||
0 |
0 |
0 |
|||
1 |
0 |
0 |
|||
0 |
1 |
0 |
|||
0 |
0 |
1 |
|||
0 |
-1 |
-1 |
|||
0 |
0 |
0 |
|||
t
5 3
3
3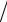 2
2
Из таблицы видно, что разрешающим столбцом является
столбец |
a |
2 |
, а разрешающей строкой |
a |
8 |
. Заменяем в базисе век- |
||||
|
|
|||||||||
тор a |
8 |
на вектор a |
2 |
и строим новую симплексную таблицу: |
||||||
|
|
|||||||||
базис |
c |
b xb |
0 |
0 |
|||
|
a |
1 |
a |
2 |
|||
|
|
|
|
|
|
||
a |
6 |
0 |
1 2 |
1 |
0 |
||
|
|
|
|
|
|
|
|
a |
7 |
0 |
9 2 |
-1 |
0 |
||
|
|
|
|
|
|
|
|
a |
2 |
0 |
3 2 |
0 |
1 |
||
|
|
|
|
|
|
|
|
a |
9 |
-1 |
2 |
0 |
0 |
|
|||||
z |
|
-2 |
0 |
0 |
|
|
|
|
0 |
0 |
|
0 |
0 |
||
a |
3 |
a |
4 |
|
|
||
0 |
1 2 |
||
0 |
1 2 |
||
0 |
1 2 |
||
1 |
-2 |
||
-1 |
2 |
||
-1 |
2 |
||
0
a |
5 |
|
3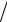 2
2
1 2
2
1 2
2
0 |
0 |
0 |
0
a |
6 |
|
|
1 |
|
0
0
0
0
0
0
a |
7 |
|
0
1
0
0 |
0 |
0 |
-1 -1 t
a |
8 |
a |
9 |
|
|
||
3 2 |
0 |
||
1 2 |
0 |
||
1 2 |
0 |
||
0 |
1 |
0 |
-1 |
1 |
0 |
Заменяем в базисе вектор симплексную таблицу:
a |
9 |
|
на вектор
a |
3 |
|
и строим новую
|
c |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
t |
базис |
|
b xb |
a1 |
a 2 |
a3 |
a 4 |
a5 |
a6 |
a7 |
a8 |
a9 |
|
a6 |
0 |
1 2 |
1 |
0 |
0 |
1 2 |
3 2 |
1 |
0 |
3 2 |
0 |
|
a7 |
0 |
9 2 |
-1 |
0 |
0 |
1 2 |
1 2 |
0 |
1 |
1 2 |
0 |
|

74
|
|
c |
b xb |
базис |
0 |
||
a |
2 |
3 2 |
|
|
|
|
|
a |
3 |
0 |
2 |
|
|
|
|
z |
|
0 |
|
|
|
|
|
Вектор |
|
0
a |
1 |
|
|
0 |
|
0 |
|
0
0
0 ,
0 |
0 |
||
a |
2 |
a |
3 |
|
|
||
1 |
0 |
||
0 |
1 |
||
0 |
0 |
||
0 |
0 |
||
поэтому
0
a |
4 |
|
|
1 2 |
|
-2
0
0
точка
0
a |
5 |
|
|
1 2 |
|
0 |
|
0
0
~ x
|
0 |
0 |
||
|
a |
6 |
a |
7 |
|
|
|
||
|
0 |
0 |
||
|
0 |
0 |
||
|
0 |
0 |
||
|
0 |
0 |
||
|
0;3 2; 2;0; |
|||
-1 |
-1 |
||
a |
8 |
a |
9 |
|
|
||
1 2 |
0 |
||
0 |
1 |
||
0 |
0 |
||
1 |
1 |
||
0;1 2;9
2;9 2;0;
2;0;
t
0
является |
решением вспомогательной задачи (з2). Тогда точка |
|
~ |
0;3 |
2; 2;0;0;1 2;9 2 является начальной крайней точкой за- |
x0 |
||
дачи линейного программирования в канонической форме (з1).
Приступим к решению задачи (з1). Составим первую симплексную таблицу для начальной крайней точки
~ |
0;3 2; 2;0;0;1 2;9 |
2 . Разложения векторов |
x0 |
возьмем из последней симплексной таблицы:
1 |
, a |
4 |
, a |
5 |
b, a |
|
|
базис
a |
6 |
|
|
a |
7 |
|
|
a |
2 |
|
|
a |
3 |
|
|
z |
|
|
|
c
0
0
-1
1
b x |
|
2 |
-1 |
1 |
0 |
-1 |
0 |
0 |
t |
|||||||
a |
1 |
a |
2 |
a |
3 |
a |
4 |
a |
5 |
a |
6 |
a |
7 |
|
||
b |
|
|
|
|
|
|
|
|
|
|||||||
1 2 |
|
1 |
0 |
0 |
1 2 |
3 2 |
1 |
0 |
|
|||||||
9 2 |
|
-1 |
0 |
0 |
1 2 |
1 2 |
0 |
1 |
|
|||||||
3 2 |
|
0 |
1 |
0 |
1 2 |
1 2 |
0 |
0 |
|
|||||||
2 |
|
0 |
0 |
1 |
-2 |
0 |
0 |
0 |
|
|||||||
1 2 |
|
0 |
-1 |
1 |
3 2 |
1 2 |
0 |
0 |
|
|||||||
|
|
-2 |
0 |
0 |
3 2 |
3 2 |
0 |
0 |
|
|||||||
Из таблицы видно, что разрешающим столбцом является столбец a1 , а разрешающей строкой a6 . Заменяем в базисе вектор a6 на вектор a1 и строим новую симплексную таблицу:
базис
a |
1 |
|
a7
a 2
c
2
0
-1
b xb
1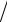 2
2
5
3 2
2
a |
1 |
|
1 |
0 |
0
-1
a |
2 |
|
0 |
0 |
1
1 0
a3 |
a 4 |
0 |
1 2 |
0 |
0 |
0 1 2
-1 0
a5 |
a6 |
3 2 |
1 |
1 |
1 |
1 2 0
0
a |
7 |
|
0 |
1 |
0
t

75
базис
a |
3 |
|
|
z |
|
c
1
b x |
|
b |
|
2 |
|
3 2 |
|
2
a |
1 |
|
0
2
0
-1
a |
2 |
|
0
-1
0
1 |
0 |
-1 |
|||
a |
3 |
a |
4 |
a |
5 |
|
|
|
|||
1 |
-2 |
0 |
|||
1 |
1 2 |
7 2 |
|||
0 |
1 2 |
9 2 |
|||
0 |
0 |
||
a |
6 |
a |
7 |
|
|
||
0 |
0 |
||
2 |
0 |
||
2 |
0 |
||
|
|
|
|
t
Далее заменяем в базисе вектор новую симплексную таблицу:
a |
1 |
|
на вектор
a |
4 |
|
и строим
c
базис
a |
4 |
0 |
|
|
|
a |
7 |
0 |
|
|
|
a |
2 |
-1 |
|
|
|
a |
3 |
1 |
|
|
|
z |
|
|
|
|
|
Так как
b xb
1
5
2
4
2
0
|
2 |
-1 |
1 |
0 |
|
|
a1 |
a 2 |
a3 |
a 4 |
|
|
2 |
0 |
|
0 |
1 |
|
0 |
0 |
|
0 |
0 |
|
1 |
1 |
|
0 |
0 |
|
4 |
0 |
|
1 |
0 |
|
3 |
-1 |
1 |
0 |
|
|
1 |
0 |
|
0 |
0 |
, то точка |
0;2;4;1;0;0;5 |
||||
-1 |
0 |
0 |
t |
a5 |
a6 |
a7 |
|
3 |
2 |
0 |
|
1 |
1 |
1 |
|
1 |
1 |
0 |
|
6 |
4 |
0 |
|
5 |
3 |
0 |
|
6 |
3 |
0 |
|
|
|
|
|
является решением за-
дачи (з1). Тогда точка
xˆ 0;2;4;1;0
является решением исходной
задачи (з).
Ответ:
x 0;2;4;1;0 abs min з, |
S |
|
ˆ |
|
min |
|
|
2
.
●
Задачи для самостоятельного решения
Решить симплекс-методом задачи линейного программирования в канонической форме с заданной начальной крайней точкой:
6.1. f x 2x1 x
|
x1 2x2 |
||
|
x |
x |
2 |
|
1 |
|
|
x |
0, i 1, |
||
i |
|
|
|
23x3 x4 max ;
5x3 x4 4 ,
x3 |
2x4 1, |
... ,4 |
, x0 0;0;1;1 |
6.2. f x 6x1 x2 4x3 5x4 max ; 3x1 x2 x3 x4 4,
5x1 x2 x3 x4 4 ,
76
|
xi 0, i 1, ... ,4 |
, |
x0 |
1;0;0;1 |
||
6.3. |
f x x1 x2 x3 |
x4 |
x5 max ; |
|||
|
2x1 3x2 5x3 7x4 9x5 19 , |
|||||
|
x1 x2 x4 2x5 2, |
|
||||
|
xi 0, i 1, ... ,5, |
|
x0 0;0;1;2;0 |
|||
6.4. |
f x x1 2x2 |
2x3 x4 6x5 |
max |
|||
|
x1 3x2 3x3 x4 9x5 18 |
, |
||||
|
x1 5x2 2x4 8x5 13, |
|
||||
|
x |
x |
|
3 |
|
|
|
3 |
5 |
x0 0;1;2;0;1 |
|||
|
xi 0, i 1, ... ,5, |
|||||
;
Решить задачу линейного программирования симплексметодом, находя начальную крайнюю точку методом искусственного базиса:
6.5. |
x1 4x2 x3 max ; |
|
x1 x2 x3 3, |
|
2x1 5x2 x3 0, |
|
xi 0, i 1, ... ,3. |
6.6. |
f x 6x1 8x2 x3 3x4 min ; |
|
2x1 5x2 x3 2x4 20 , |
|
12x1 6x2 2x3 x4 72 , |
|
xi 0, i 1, ... ,4 |
Указание: привести предварительно задачу к канонической |
|
форме. |
f x x1 4x4 max ; |
6.7. |
|
|
x1 2x2 2x3 x4 5x5 13, |
|
2x1 2x2 4x4 x5 5, |
|
x1 x2 x3 x4 2x5 5 |
xi 0, i 1, ... ,5.
77
Найти решение задач линейного программирования:
6.8.
6.9.
6.10.
f
f x x1 |
x2 |
x3 min |
; |
||||||||||||
|
x1 3x2 5x3 1, |
|
|
|
|||||||||||
|
x1 x2 x3 3, |
|
|
|
|
||||||||||
|
2x |
x |
2 |
|
4x |
0 |
|
|
|
||||||
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
xi |
0, i 1,2,3. |
|
|
|
|
|
||||||||
x 2x x |
2 |
3x |
5x |
4 |
max |
||||||||||
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|||
2x1 3x2 x3 2x4 30 |
, |
|
|||||||||||||
4x1 2x2 x3 2x4 40 |
, |
|
|||||||||||||
x1 2x2 3x3 x4 25, |
|
||||||||||||||
|
xi 0, i 1, ... ,4 |
|
|
|
|
|
|||||||||
f x 2x |
|
x |
2 |
x |
3 |
x |
5 |
min |
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
2x |
|
x |
|
x |
3, |
|
|
|
|
|
||||
|
2 |
|
|
4 |
|
5 |
|
|
|
|
|
|
|
||
|
x |
|
2x |
2, |
|
|
|
|
|
||||||
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
x1 3x2 x4 5, |
|
|
|
|
||||||||||
x |
x 3, x |
j |
0, j 1,...,5 |
|
|||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;
;
Занятие 7. Транспортная задача
Транспортная задача является важным частным случаем задачи линейного программирования. Она представляет собой математическую модель задач по оптимизации перевозок.
Постановка
A1, A2 ,..., Am , на
задачи. Имеется |
m |
станций отправления |
которых сосредоточено соответственно
a1, a2 ,..., am единиц некоторого однородного груза. Этот груз следует перевезти в n пунктов назначения B1, B2 ,..., Bn , причем в каждый из них надлежит завезти соответственно b1,b2 ,...,bn единиц груза. Стоимость перевозки единицы груза из пункта Ai в пункт B j равна cij .
78
Обозначим через
xij
количество единиц груза, предназна-
ченного к отправке из пункта
Ai
в пункт
B j
. Получим задачу о
нахождении плана перевозок, при котором общая стоимость перевозок окажется минимальной:
m n
cij xij min ;
i1 j 1
n |
|
|
xij ai , |
i 1,..., m ; |
|
j 1 |
|
|
m |
|
|
xij |
b j , |
j 1,..., n ; |
j 1 |
|
|
xij 0, |
i 1,..., m, j 1,..., n . |
|
(з)
(1)
(2)
Условие (1) означает, что из пункта
Ai
весь груз вывезен в
пункты назначения, а завезенного в пункт
условие (2) означает, что количество груза, B j со всех пунктов отправления, соответ-
ствует требуемому. Транспортную задачу удобно записывать в виде платежной матрицы:
|
b |
b |
… |
b |
|
1 |
2 |
|
n |
a |
c |
c |
… |
c1n |
1 |
11 |
12 |
|
|
a2 |
c21 |
c22 |
… |
c2n |
… |
… |
… |
… |
… |
am |
cm1 |
cm2 |
… |
cmn |
m |
m n |
n m |
n |
В поставленной задаче ai xij xij b j . В |
|||
i 1 |
i 1 j 1 |
j 1i 1 |
j 1 |
этом случае говорят, что задана замкнутая модель транспортной задачи.
Если суммарные запасы пунктов отправления больше сум-
m |
n |
марной потребности пунктов назначения, т.е. ai b j , то ра- |
|
i 1 |
j 1 |
79
|
n |
|
венства (1) заменяются неравенствами: |
xij |
ai |
|
j 1 |
|
условия (2) остаются без изменений. В этом случае к замкнутой модели следует:
а) ввести фиктивный пункт назначения |
Bn 1 |
|
m |
n |
|
величиной ввоза bn 1 ai b j ; |
|
|
i 1 |
j 1 |
|
,
i 1,..., m , а
для сведения с требуемой
б) положить ci,n 1 0, i 1,..., m; |
|
в) ввести дополнительные переменные |
xi,n1 0, i 1,..., m . |
Тогда придем к замкнутой модели транспортной задачи.
Если в задаче имеется дополнительное требование, состоящее в том, что из некоторого пункта Ai груз должен быть полностью вывезен, то стоимость перевозки единицы груза из пункта
Ai в пункт Bn 1 следует положить равной |
M , где M - достаточ- |
|
но большое положительное число, т.е. ci,n 1 M . |
||
Если суммарные запасы отправителей меньше суммарных |
||
|
m |
n |
запросов пунктов назначения, т.е. ai |
b j , то равенства (2) |
|
|
i 1 |
j 1 |
заменяются неравенствами: |
|
|
m |
|
|
xij b j , j 1,..., n, а условия (1) остаются без изменений. В |
||
i 1 |
|
|
этом случае для сведения к замкнутой модели следует: |
||
а) вести фиктивный пункт отправления Am 1 с требуемой |
||
n |
m |
|
величиной вывоза am 1 b j ai ; |
|
|
j 1 |
i 1 |
|
б) положить cm 1, j 0, |
j 1,..., n ; |
|
в) ввести дополнительные переменные xm 1, j 0, j 1,..., n . Тогда придем к замкнутой модели транспортной задачи.
80
Если в задаче имеется дополнительное требование |
полно- |
стью удовлетворить потребности пункта назначения B j , |
то сле- |
дует положить |
cm1, j |
жительное число.
M
, где
M
