3. Более удобными (по сравнению с уравнением и уравнением ) являются каноническое и параметрические уравнения прямой. Эти уравнения получаются из решения следующей задачи.

Задача 2. Найти прямую, проходящую через точку параллельно вектору .

Решение. Обозначим искомую прямую через .

координаты векторов пропорциональны

. Полученное уравнение называется каноническим уравнением прямой на плоскости. При решении задачи главную роль сыграло условие коллинеарности двух векторов. Это условие использовалось в формулировке: два вектора параллельны тогда и только тогда, когда пропорциональны из координаты.

Если при решении этой же задачи использовать условие коллинеарности двух векторов в виде: , то получим,

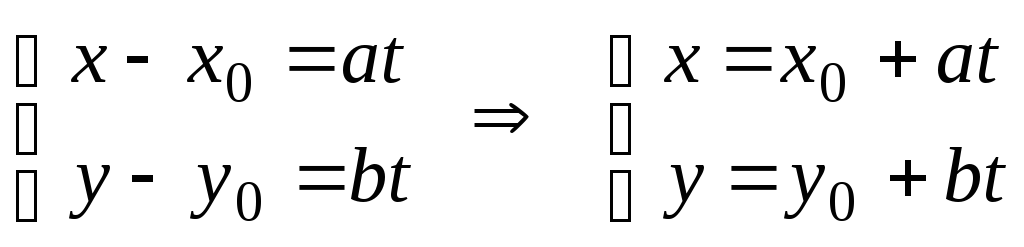. Такая система равенств называется параметрическими уравнениями прямой на плоскости.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

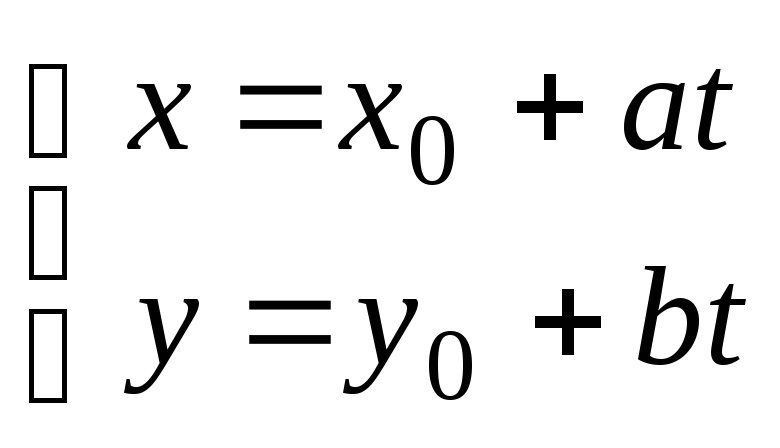Каноническое уравнение и параметрические уравнения прямой имеют то преимущество над уравнением и общим уравнением прямой , что из канонического и параметрических уравнений прямой видна точка , лежащая на прямой, и направляющий вектор . Например,

1) - каноническое уравнение прямой, проходящей через точку параллельно вектору ,

2) - каноническое уравнение прямой, проходящей через точку параллельно вектору ,

3) 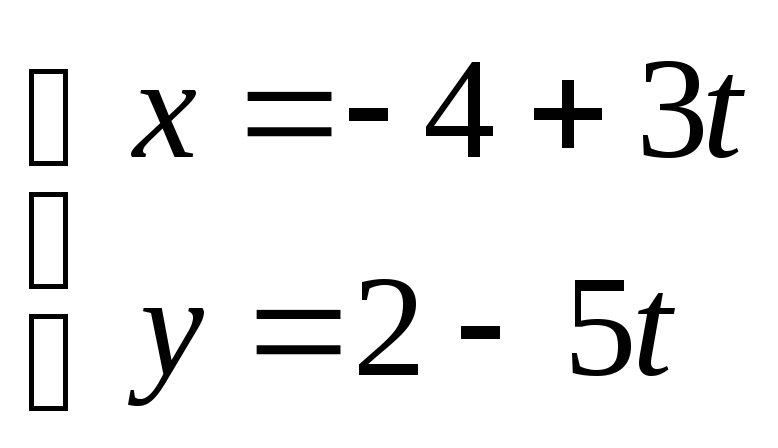- параметрические уравнение прямой, проходящей через точку параллельно вектору ,

4) - параметрические уравнение прямой, проходящей через точку параллельно вектору .

Из канонического или параметрических уравнения прямой на плоскости легко найти общее уравнение прямой и уравнение вида . Например,

1) - каноническое уравнение прямой - общее уравнение прямой - уравнение прямой с угловым коэффициентом наклона.

2) - - параметрические уравнение прямой - каноническое уравнение прямой - общее уравнение прямой

- уравнение прямой с угловым коэффициентом наклона.

Все многочисленные задачи по нахождению уравнения прямой на плоскости могут быть сведены к решению задачи 1 или задачи 2. Покажем это на следующих примерах.

Пример 3. Найти общее уравнение прямой, проходящей через точки .

Решение. - направляющий вектор искомой прямой. Теперь решаемую задачу можно сформулировать в виде рассмотренной выше задачи 2: найти общее уравнение прямой, проходящей через точку параллельно вектору

. Обозначим искомую прямую через , тогда:

координаты векторов пропорциональны

- каноническое уравнение прямой - общее уравнение искомой прямой.

Пример 4. Найти общие уравнения двух прямых, проходящих через точку параллельно и перпендикулярно прямой :.

Решение. Пусть - прямая, проходящая через точкупараллельно прямой, и - прямая, проходящая через точку перпендикулярно прямой . Из уравнения прямой находим нормальный к этой прямой вектор . Этот вектор является вектором нормали к прямой и направляющим вектором для прямой . Поэтому, нахождение прямой повторяет решение задачи 1, а нахождение прямой повторяет решение задачи 2.

1)

первый ответ: - общее уравнение прямой .

2) координаты векторов пропорциональны

- каноническое уравнение прямой

второй ответ: - общее уравнение прямой .

Пример 5. Пусть точки - вершины треугольника . Найти канонические уравнения следующих четырех прямых: идущих по стороне , по высоте, медиане и биссектрисе треугольника из вершины .

Решение.

1) Обозначим прямую, идущую по стороне через . Нахождение канонического уравнения этой прямой проводится аналогично решению задачи из примера 3.

- направляющий вектор искомой прямой .

координаты векторов пропорциональны

ответ: - каноническое уравнение прямой .

2) Обозначим прямую, идущую по высоте треугольника из вершины через .

Направляющий вектор прямой является вектором нормали к прямой . По вектору нетрудно найти направляющий вектор прямой . Действительно, скалярное произведение этих векторов равно нулю. Пусть , тогда из можно взять . Найдем уравнение прямой , проходящей через точку параллельно вектору :

координаты векторов пропорциональны

ответ: - каноническое уравнение прямой .

3) Обозначим прямую, идущую по медиане треугольника из вершины через .

Найдем еще одну точку на прямой . В качестве этой точки можно точку - срединную точку отрезка : .

- направляющий вектор прямой . Дальнейшие рассуждения таковы:

координаты векторов пропорциональны

ответ: - каноническое уравнение прямой .

4) Обозначим прямую, идущую по биссектрисе треугольника из вершины через . Найдем направляющий вектор прямой . Сначала найдем векторы ,

, затем их орты ,

. Сумма ортов - вектор, направленный по диагонали параллелограмма, построенного на векторах . Т.к. эти векторы имеют одинаковую длину , то параллелограмм является ромбом, а диагональ ромба является одновременно его биссектрисой. Следовательно, вектор

- направляющий вектор прямой . Вместо вектора в качестве направляющего вектора прямой лучше взять вектор . Найдем уравнение прямой .

координаты векторов пропорциональны

ответ: - каноническое уравнение прямой .

Пример 6. Стороны треугольника лежат на прямых заданных общими уравнениями. .

Найти длину высоты этого треугольника из вершины .

Решение. Сначала найдем вершину , которая служит точкой пересечения прямых и . Поскольку эта точка лежит на обеих прямых, ее координаты можно определить из системы . Решение этой системы найдем по правилу Крамера:

.

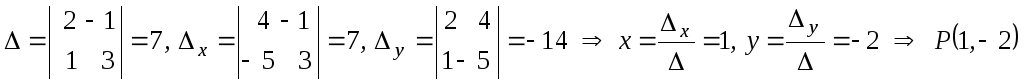Из уравнения прямой находим нормальный к ней вектор , который будет параллелен прямой , идущей по высоте , т.е. является направляющим вектором прямой . Найдем общее уравнение прямой .

координаты векторов пропорциональны

- каноническое уравнение прямой

- общее уравнение прямой .

Теперь найдем точку пересечения прямых и , как решение системы

. Эту систему тоже решим по правилу Крамера.

.

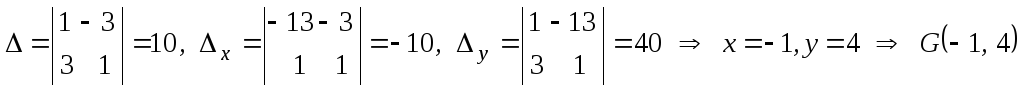Точка является проекцией точки на прямую .

.