
Занятие 9(Фдз 10)
.doc
Занятие 9 (Фдз 10).
Приведение квадратичной формы к каноническому и нормальному виду методом Лагранжа.
9.1. Канонический и нормальный вид квадратичной формы. Получение нормального вида из канонического. Теорема о приведении квадратичной формы к каноническому виду. Метод Лагранжа приведения квадратичной формы к каноническому виду. Положительный и отрицательный индексы, ранг квадратичной формы. Закон инерции. Три инварианта квадратичной формы.
9.1. Квадратичная форма вида
![]() (1)
(1)
называется
канонической.
Если в каноническом виде (1) квадратичной
формы коэффициенты
![]() равны либо
равны либо
![]() ,
либо
,
либо
![]() ,
либо 0, то такую квадратичную форму
называют
,
либо 0, то такую квадратичную форму
называют
нормальной. Матрица квадратичной формы в каноническом или нормальном виде является диагональной матрицей.
Линейным
преобразованием координат
![]()
![]()
![]() называется преобразование вида
называется преобразование вида
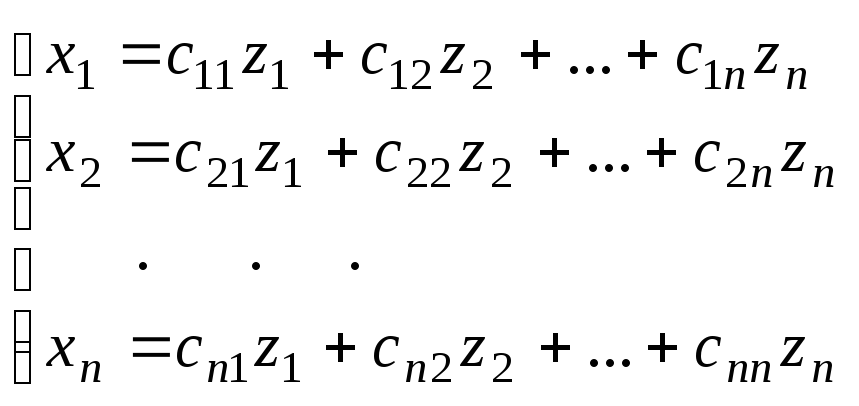 или в матричном
виде
или в матричном
виде
 .
(2)
.
(2)
 называется матрицей
линейного преобразования. Линейное
преобразование (2) называется невырожденным,
если определитель матрицы
называется матрицей
линейного преобразования. Линейное
преобразование (2) называется невырожденным,
если определитель матрицы
![]() отличен от нуля.
отличен от нуля.
В результате применения преобразования (2) квадратичная форма меняется по закону
![]() ,
где
,
где
 ,
,
![]() .
(3)
.
(3)
Теорема Лагранжа (о приведении квадратичной формы к каноническому виду). Любую квадратичную форму можно линейным невырожденным преобразованием координат (2) привести к каноническому виду.
Основывающийся на этой теореме метод Лагранжа приведения квадратичной формы к каноническому виду посредством преобразований (2) заключается в последовательном выделении из квадратичной формы полных квадратов. Действие этого метода продемонстрируем на примерах ниже.
Ранг
![]() квадратичной формы
квадратичной формы
![]() совпадает с рангом матрицы этой формы.
Проще всего
совпадает с рангом матрицы этой формы.
Проще всего
![]() находится из канонического вида (1)
квадратичной формы:
находится из канонического вида (1)
квадратичной формы:
![]() ,
где
,
где
![]() -
число ненулевых коэффициентов
-
число ненулевых коэффициентов
![]() в
(1).
в
(1).
Число
![]() положительных коэффициентов
положительных коэффициентов
![]() в
(1) называется
положительным индексом инерции,
число
в
(1) называется
положительным индексом инерции,
число
![]() отрицательных коэффициентов
отрицательных коэффициентов
![]() в
(1) называется
отрицательным индексом инерции
квадратичной формы.
в
(1) называется
отрицательным индексом инерции
квадратичной формы.
Квадратичные
формы подчиняются закону
инерции,
согласно которому положительный и
отрицательный индексы инерции не зависят
от способа приведения квадратичной
формы линейными преобразованиями
координат к каноническому виду (1) и
всегда принимают одни и те же значения.
Таким образом, величины
![]() и
и
![]() являются
инвариантами квадратичной
формы.
являются
инвариантами квадратичной
формы.
Ранг
![]() квадратичной формы можно найти по
индексам инерции:
квадратичной формы можно найти по
индексам инерции:
![]() .
.
Еще одним инвариантом
квадратичной
формы служит
число
![]() нулевых коэффициентов
нулевых коэффициентов
![]() в
(1). Величина
в
(1). Величина
![]() также не зависит от того, каким линейным
преобразованием координат квадратичная
форма приведена к каноническому виду.
также не зависит от того, каким линейным
преобразованием координат квадратичная
форма приведена к каноническому виду.
В начале приведем примеры квадратичных форм в каноническом и нормальном виде с указанием их ранга и трех инвариантов.
1)
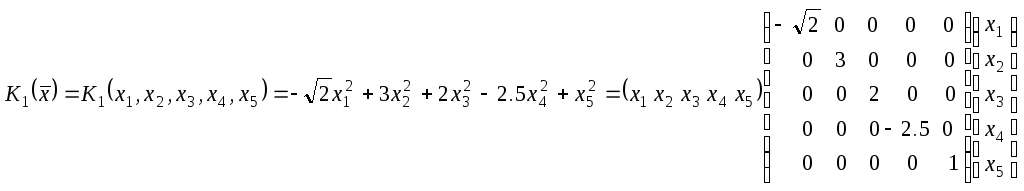 - квадратичная форма канонического
вида,
- квадратичная форма канонического
вида,
![]() - ранг квадратичной формы
- ранг квадратичной формы
![]() ,
,
![]() - инварианты этой формы.
- инварианты этой формы.
2)
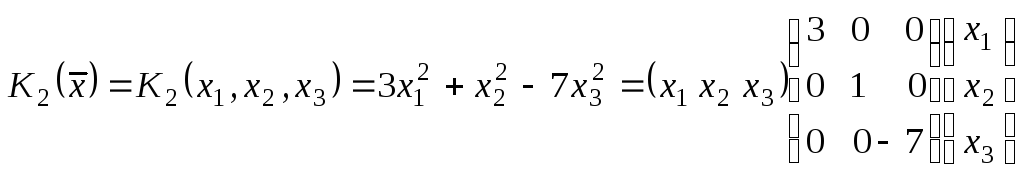 - квадратичная форма канонического
вида,
- квадратичная форма канонического
вида,
![]() - ранг
- ранг
![]() ,
,
![]() - инварианты
- инварианты
![]() .
.
3)
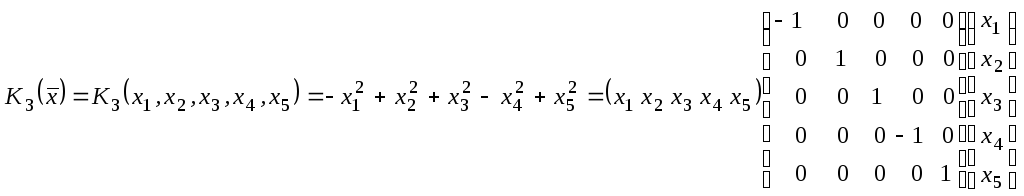 -
-
квадратичная форма
нормального вида,
![]() - ранг
- ранг
![]() ,
,
![]() - инварианты
- инварианты
![]() .
.
4)
 - квадратичная форма нормального вида,
- квадратичная форма нормального вида,
![]() - ранг
- ранг
![]() ,
,
![]() - инварианты
- инварианты
![]() .
.
5)
 - квадратичная форма нормального вида,
- квадратичная форма нормального вида,
![]() - ранг
- ранг
![]() ,
,
![]() - инварианты
- инварианты
![]() .
.
6)
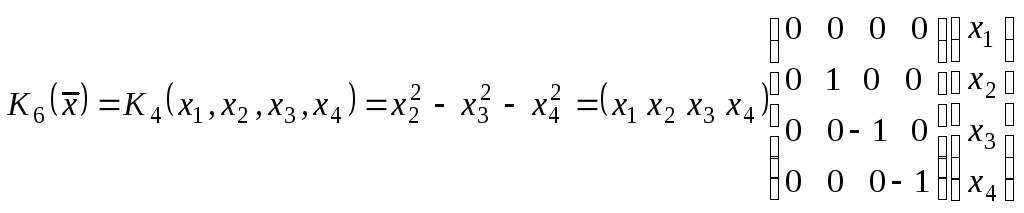 - квадратичная форма нормального вида,
- квадратичная форма нормального вида,
![]() - ранг
- ранг
![]() ,
,
![]() - инварианты
- инварианты
![]() .
.
Теперь на примерах ниже изложим метод Лагранжа приведения квадратичной формы к каноническому виду.
Пример 1. Методом Лагранжа привести к каноническому виду квадратичную форму
![]() .
Найти также нормальный вид и инварианты
.
Найти также нормальный вид и инварианты
![]() .
.
Решение.
![]() содержит слагаемое
с
содержит слагаемое
с
![]() .
Это позволяет выделить полный квадрат
из слагаемых, содержащих координату
.
Это позволяет выделить полный квадрат
из слагаемых, содержащих координату
![]() .
.
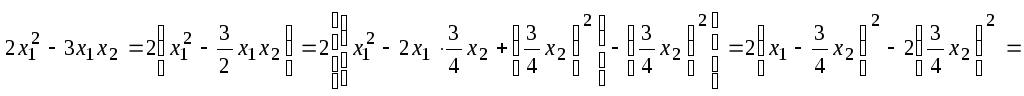
![]()
![]()
![]() - канонический
вид квадратичной формы.
(4)
- канонический
вид квадратичной формы.
(4)
Этот канонический вид получен после замены
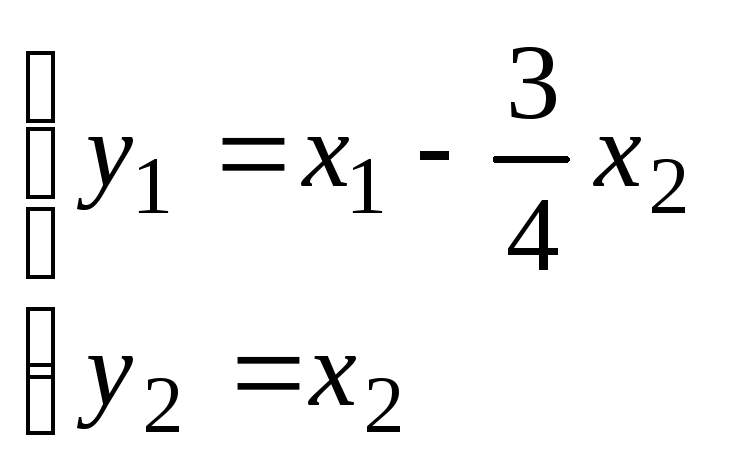 .
.
Из уравнений замены находится невырожденное линейное преобразование координат
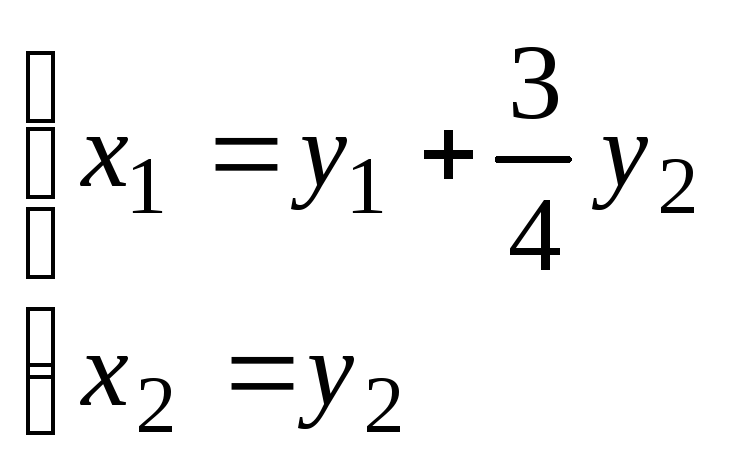 ,
(5)
,
(5)
приводящее заданную квадратичную форму к каноническому виду (4).
Проверка.
![]()
![]() .
.
Результаты проверки доказывают справедливость сделанных выводов.
Теперь, пользуясь каноническим видом (4), найдем нормальный вид квадратичной формы.
(4)
![]() - нормальный вид квадратичной формы.
- нормальный вид квадратичной формы.
Здесь
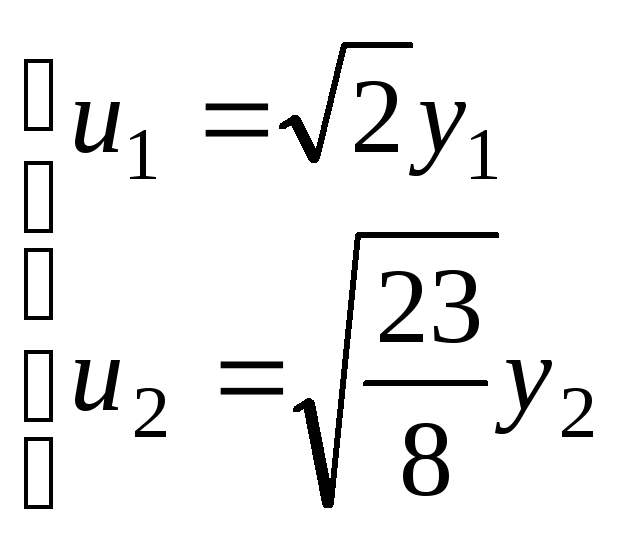 .
.
Приведем другое решение поставленной задачи.
![]() содержит слагаемое
с
содержит слагаемое
с
![]() .
Поэтому метод Лагранжа можно начать с
выделения полного квадрата из слагаемых,
содержащих координату
.
Поэтому метод Лагранжа можно начать с
выделения полного квадрата из слагаемых,
содержащих координату
![]() .
.
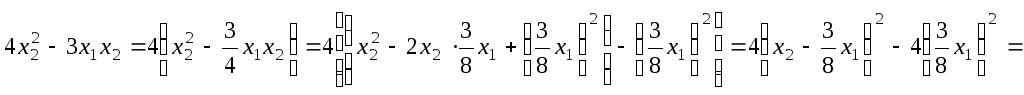
![]()
![]() - канонический
вид квадратичной формы.
(6)
- канонический
вид квадратичной формы.
(6)
Этот канонический вид получен в результате невырожденного линейного преобразования
 .
(7)
.
(7)
(6)
![]() - нормальный вид квадратичной формы.
- нормальный вид квадратичной формы.
Здесь
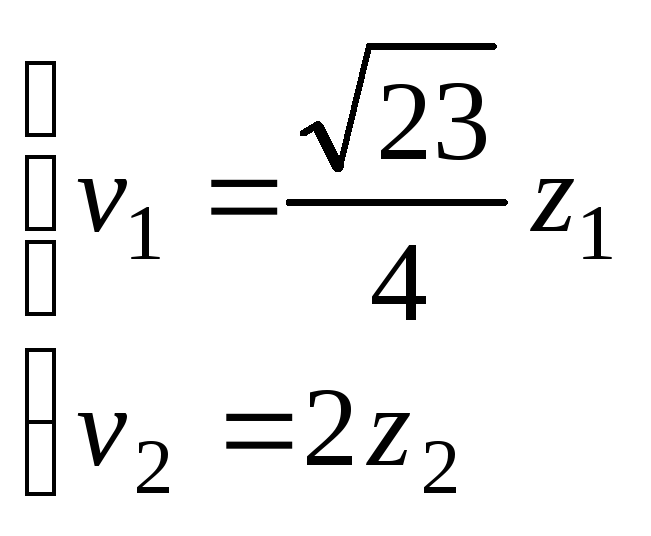 .
.
Канонический вид (4) отличается от канонического вида (6). Проведенные решения показывают, что метод Лагранжа может проходить различными способами и приводить заданную квадратичную форму к различным каноническим видам. Однако все ответы должны подчиняться закону инерции. Из (4) и (6) следует такой общий результат:
![]() - инварианты
квадратичной формы.
- инварианты
квадратичной формы.
Пример 2. Методом Лагранжа привести к каноническому виду квадратичную форму
![]() .
Найти также нормальный вид
.
Найти также нормальный вид
![]() и ее индексы инерции.
и ее индексы инерции.
Решение.
![]() содержит слагаемое
с
содержит слагаемое
с
![]() .
Поэтому, начнем метод Лагранжа с выделения
полного квадрата из слагаемых, содержащих
координату
.
Поэтому, начнем метод Лагранжа с выделения
полного квадрата из слагаемых, содержащих
координату
![]() .
.
![]()
![]()
![]() .
.
Сумма
![]() ,
стоящая после выделенного квадрата,
содержит член с
,
стоящая после выделенного квадрата,
содержит член с
![]() .
.
Поэтому, в этой
сумме можно выделить полный квадрат из
слагаемых с координатой
![]() .
.
![]()
![]()
![]() - канонический
вид квадратичной формы.
(8)
- канонический
вид квадратичной формы.
(8)
Здесь
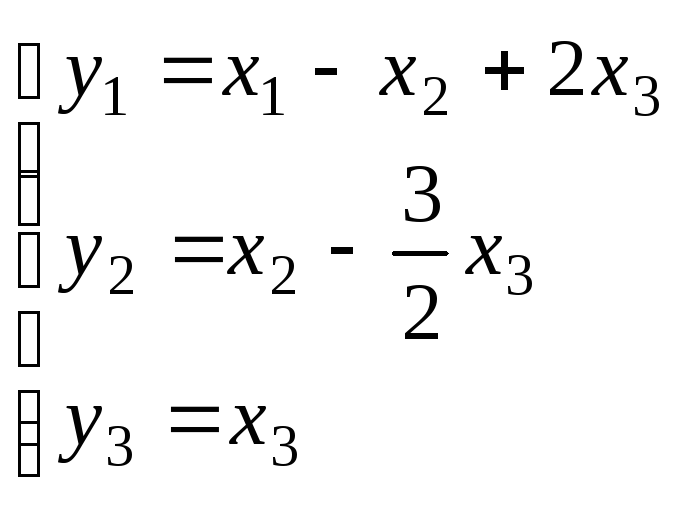 .
.
Из этих формул, поднимаясь по уравнениям снизу вверх, находится линейное преобразование координат, приводящее заданную квадратичную форму к каноническому виду (8)
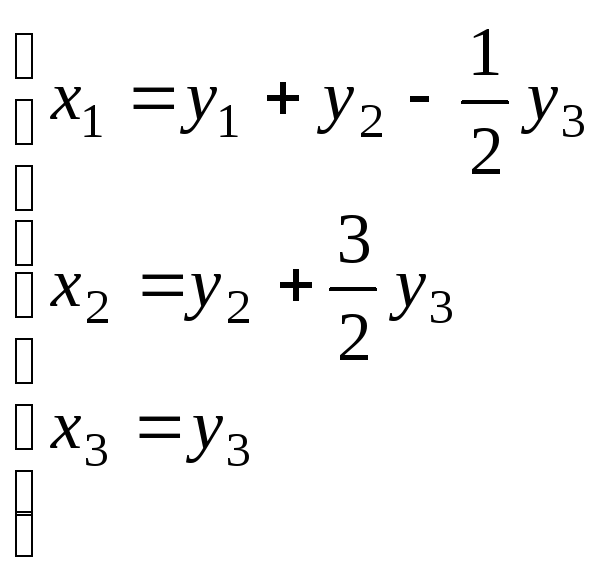 .
(9)
.
(9)
(8)
![]() - нормальный вид квадратичной формы.
- нормальный вид квадратичной формы.
![]() - индексы инерции квадратичной формы.
- индексы инерции квадратичной формы.
Пример 3. Методом Лагранжа привести к каноническому виду квадратичную форму
![]() .
Найти также нормальный вид и инварианты
.
Найти также нормальный вид и инварианты
![]() .
.
Решение.
В данной квадратичной
форме нет слагаемых с квадратами
координат, и присутствуют только
смешанные члены. В этом случае необходимо
применить специальное линейное
преобразование координат, позволяющее
получить слагаемые с квадратами
координат. Наличие смешанного члена с
![]() позволяет использовать такое специальное
линейное преобразование
позволяет использовать такое специальное
линейное преобразование
 или в матричной
форме
или в матричной
форме
 .
(10)
.
(10)
![]()
![]() .
.
Теперь можно выделить полные квадраты аналогично тому, как это делалось в примерах выше.
![]() .
.
![]() .
.
![]()
![]()
![]()
![]() - канонический
вид квадратичной формы.
(11)
- канонический
вид квадратичной формы.
(11)
Здесь
 .
(12)
.
(12)
Из (10), (12) находим невырожденное линейное преобразование, приводящее заданную квадратичную форму к каноническому виду (11).
 ,
где
,
где
![]() .
.
Вычисление матрицы
![]() линейного преобразования предоставляем
читателю.
линейного преобразования предоставляем
читателю.
(11)
![]() - инварианты квадратичной формы.
- инварианты квадратичной формы.
Пример 4. Методом Лагранжа привести к каноническому виду квадратичную форму
![]() .
Найти также нормальный вид и инварианты
квадратичной формы.
.
Найти также нормальный вид и инварианты
квадратичной формы.
Решение.
Сначала выделим
полный квадрат из слагаемых с координатой
![]() .
.
![]()
![]() .
.
![]() .
.
За выделенным
квадратом стоит сумма из смешанных
членов
![]() и
и
![]() .
.
Следующий ход в
методе Лагранжа – специальное линейное
преобразование координат. Сделаем его
на основе слагаемого
![]() .
.
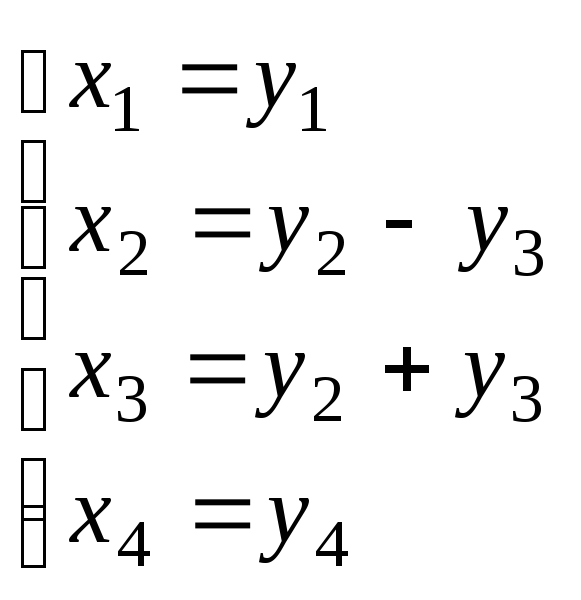 или
или
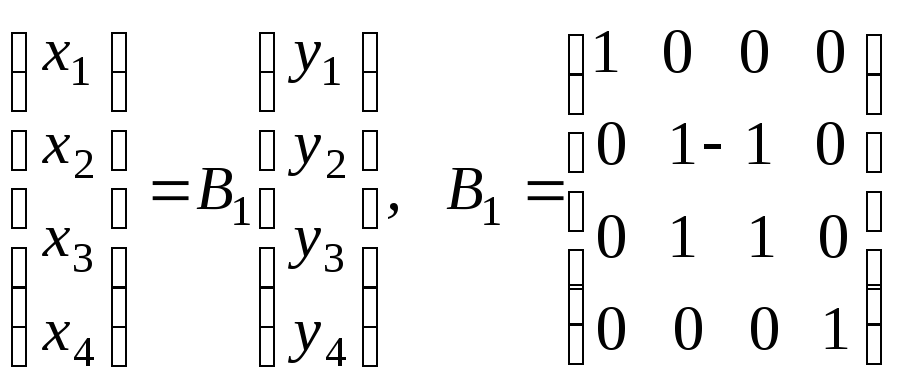 .
(13)
.
(13)
![]()
![]() .
.
Теперь можно
выделить полный квадрат из суммы
![]() ,
содержащей слагаемые с координатой
,
содержащей слагаемые с координатой
![]() .
.
![]() .
.
![]() .
.
Теперь выделим
полный квадрат из суммы
![]() ,
содержащей слагаемые с координатой
,
содержащей слагаемые с координатой
![]() .
.
![]() .
.
![]()
![]()
![]() - канонический
вид квадратичной формы.
(14)
- канонический
вид квадратичной формы.
(14)
Здесь
 или
или
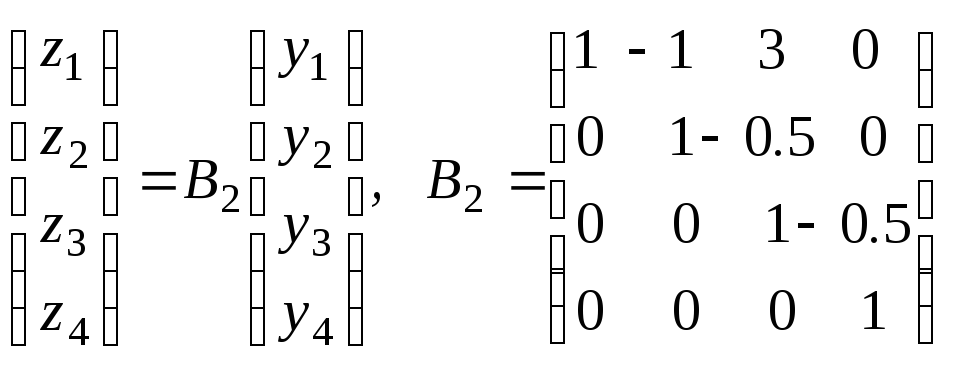 .
(15)
.
(15)
(13), (15)
![]()
 - линейное преобразование, приводящее
квадратичную форму
- линейное преобразование, приводящее
квадратичную форму
![]() к каноническому виду.
к каноническому виду.
(14)
![]() - инварианты
- инварианты
![]() .
.
(14)
![]() - нормальный вид квадратичной формы.
- нормальный вид квадратичной формы.
__________________________________________________________________________________
Домашнее задание.
1. Методом Лагранжа привести к каноническому, а затем нормальному виду квадратичные формы, приведенные ниже. Записать невырожденные преобразования координат, приводящие квадратичные формы к каноническому виду.
1.1.
![]() ,
,
![]() .
.
1.2.
![]() ,
,
![]() .
.
