Декартово произведение множеств. Отношение.

1. Отношение

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.

1.1. Одноместное отношение.

С одной переменной

1.2. Бинарное отношение

С двумя

1.3. БИНАРНЫЕ ОТНОШЕНИЯ на множестве

Понятие бинарного отношения на заданном (непустом) множестве позволяет формализовать операции попарного сравнения элементов данного множества.

Рассмотрим непустое множество X. Любое подмножество R (не путать с R - множеством вещественных чисел) из X 2 = X i X называется бинарным отношением на множестве X. Если пара (x, y) входит в R, иногда будем писать xRy и говорить, что элемент x находится в отношении R с y.

Примерами бинарных отношений на множестве R действительных чисел являются следующие подмножества из R2 = R i R.

Пример 1. {(x, y) k R2: x2 + y2 = 1}.

Пример 2. {(x, y) k R2: x # y}.

Пример 3. {(x, y) k R2: | x | = | y |}.

Пример 4. {(x, y) k R2: x = y}.

В обыденной жизни суждения типа "Иван - сын Петра", "Татьяна старше Алексея", "Воронеж южнее Москвы", <Слова "ночь" и "день" содержат одинаковое число букв> приводят к бинарным отношениям на подходящем множестве. Например, последнее суждение (остальные попробуйте формализовать сами) определяет бинарное отношение R на множестве X всех слов: xRy, если число букв в словах x и y одинаково.

2.Варианты представления бинарных отношений на множестве (матричное, грфовое)

Другой широко распространенный способ представления отношений основан на использовании ориентированных графов. При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x, y) отношения  дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y. Граф бинарного отношения  изображен на рисунке 3.

Рис. 3. Граф бинарного отношения

Для бинарных отношений, определенных на конечных множествах, часто используется матричный способ задания. Пусть на некотором конечном множестве Xзадано отношение a. Упорядочим каким-либо образом элементы множества X = {x₁, x₂, ..., x_n} и определим матрицу отношения A = [a_ij] следующим образом:

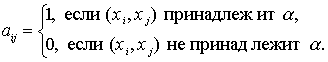
Таким образом, матрица отношения , представленного графом на рисунке 3, имеет вид

Часто матрицу отношения называют булевой, чтобы подчеркнуть, что ее элементами являются только нули и единицы.

3. Обратное бинарное отношение.

Обратное отношение (отношение, обратное к R) — это двухместное отношение, состоящее из пар элементов (у, х), полученных перестановкой пар элементов (х, у) данного отношения R.

4. Отношение функция.

Функция — двухместное отношение R, определенное на некотором множестве, отличающееся тем, что каждому значению x отношения xRy соответствует лишь одно-единственное значение y. Пример: «y отец x». Свойство функциональности отношения R записывается в виде аксиомы: (xRy и xRz)→(y≡z). Поскольку каждому значению x в выражениях xRy и xRz соответствует одно и то же значение, то y и z совпадут, окажутся одними и теми же. Функциональное отношение однозначно, поскольку каждому значению x отношения xRy соответствует лишь одно-единственное значение y, но не наоборот.

5. Оснавные свойства бинарных отношений на множестве

• В математике бинарное отношение на множестве X называется рефлексивным, если всякий элемент этого множества находится в отношении R с самим собой. Формально, отношение рефлексивно, если

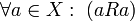
• В математике бинарное отношение на множестве X называется симметричным, если для каждой пары элементов множества выполнение отношения aRb влечёт выполнение отношения bRa.Формально, отношение симметрично, если .

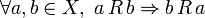
• В математике бинарное отношение на множестве называется транзитивным, если для любых трёх элементов множества выполнение отношений aRb и bRc влечёт выполнение отношения aRc.Формально, отношение транзитивно, если .

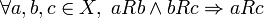
6. Транзитивное замыкание.

Транзитивное замыкание в теории множеств — это операция на бинарных отношениях. Транзитивное замыкание бинарного отношения R на множестве X есть наименьшее транзитивное отношение на множестве X, включающее R.

Например, если X — это множество людей (и живых, и мёртвых), а R — отношение «является родителем», то транзитивное замыкание R — это отношение «является предком». Если X — это множество аэропортов, а xRy эквивалентно «существует рейс из x в y», и транзитивное замыкание R равно P, то xPy эквивалентно «можно долететь из x в y самолётом» (хотя иногда придётся лететь с пересадками)

7. Отношение эквивалентности. Фактор множества.

ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ

Часто бывает, что некоторое множество является объединением своих подмножеств, никакие два из которых не имеют общих элементов (не пересекаются). В этом случае говорят, что множество разбито на непересекающиеся подмножества.

Разбиение на подмножества часто используется для классификации объектов. Например, когда составляют каталог книг в библиотеке, то все множество книг разбивают на книги по естественным наукам, общественно-политическим наукам, книги беллетристического характера и т.д.

В биологии все множество животных разбивается на типы, типы - на классы и т.д.

В математике плоскость (рассматриваемую как множество точек) можно разбить на прямые, параллельные оси абсцисс, трехмерное пространство можно представить как объединение концентрических сфер различных радиусов (начиная с r = 0).

При разбиении множества на подмножества используют понятие эквивалентности элементов. Для этого определяют, что значит "элемент x эквивалентен элементу y", после чего объединяют эквивалентные элементы в одно подмножество. При разумном понятии эквивалентности данное множество разбивается на взаимно непересекающиеся подмножества, объединение которых есть все множество.

Перейдем к формулировке соответствующих понятий. Бинарное отношение R ? X i X называется отношением эквивалентности на множестве X, если оно рефлексивно, симметрично и транзитивно.

Если R - отношение эквивалентности на X и (a, b) k R, то элементы a и b называются эквивалентными, при этом используется запись a ї b.

Из первых четырех примеров бинарных отношений на R отношениями эквивалентности являются третье и четвертое.

Рассмотрим еще несколько примеров отношений эквивалентности.

Пример 7. Пусть Z - множество целых чисел и m $ 1 - некоторое фиксированное число. Определим отношение эквивалентности R как подмножество из Z i Z, состоящее из таких пар (p, q) k Z i Z, что число p - q делится на m.

Пример 8. Пусть X = Z i N, где N - множество натуральных чисел. Отношение эквивалентности R на X определим формулой (p, q) ~ (p', q'), если pq' = p'q.

Пример 9. Пусть X - множество прямых на плоскости (или в пространстве). Определим отношение эквивалентности R на X: A ї B, если прямые A и B параллельны или совпадают. Таким образом, R состоит из упорядоченных пар прямых, которые параллельны друг другу или совпадают.

Пример 10. Пусть Y - множество направленных отрезков пространства (для направленного отрезка, соединяющего точки A и B с началом в точке A и концом в точке B, используется обозначение ). Два направленных отрезка и называются эквивалентными, если они имеют одинаковую длину, лежат на параллельных прямых и одинаково направлены. Так, введенное множество пар эквивалентных направленных отрезков является отношением эквивалентности.

Далее символом X обозначается множество, на котором задано отношение эквивалентности R.

Каждое подмножество A из X называется классом эквивалентности, если: 1) оно состоит из эквивалентных друг другу элементов и 2) если x k X эквивалентен хотя бы одному элементу из A, то x k A.

Теорема. Два класса эквивалентности либо совпадают, либо не пересекаются.

Доказательство. Пусть A и B - два класса эквивалентности из X. Допустим, что они пересекаются и c - общий элемент, то есть c k A < B. Если x - произвольный элемент из A, то x ~ c. Поскольку c k B, то и x k B. Таким образом, A ? B. Аналогично доказывается, что B ? A. Итак, A = B. Теорема доказана.

ФАКТОР-МНОЖЕСТВА

Пусть X - множество и R - отношение эквивалентности на нем. Из свойства транзитивности отношения эквивалентности следует, что любой класс эквивалентности является множеством всех элементов, эквивалентных произвольному элементу из этого класса. Таким образом, из теоремы следует, что отношение эквивалентности позволяет данное множество X представить в виде объединения взаимно непересекающихся классов эквивалентности.

Совокупность всех классов эквивалентности называется фактор-множеством. Оно обозначается символом X/R.

Как уже отмечалось, каждый элемент x из множества X полностью определяет класс эквивалентности, его содержащий, который далее обозначается символом , так что (и , если и только если x ї y). Элемент x называется представителем класса A, если x k A.

Теперь вернемся к рассмотрению примеров отношений эквивалентности и найдем соответствующие фактор-множества.

В первом примере фактор-множество состоит из m подмножеств вида

Например, при m = 2 оно состоит из двух классов: четных чисел и нечетных чисел.

Во втором примере каждый класс эквивалентности называется рациональным числом, а фактор-множество X/R - множеством рациональных чисел. Таким образом, каждое рациональное число (в обычной форме записи) есть совокупность пар (p, q) k Z i N, для которых pn = qm. Обычно рациональное число отождествляют с некоторым представителем класса эквивалентности. Множество рациональных чисел обозначим символом Q.

Сложение рациональных чисел осуществляется следующим образом: r1 + r2 = класс эквивалентности, содержащий пару (pn + mq, qn), если (p, q) k r1 и (m, n) k r2 для заданных r1 , r2 k Q. Это определение корректно, то есть не зависит от выбора представителей из r1 и r2 (почему ?). Аналогично вводится умножение рациональных чисел.

Обратимся к четвертому примеру. Каждый класс эквивалентности называется свободным вектором или просто вектором. Таким образом, вектор - это подмножество направленных отрезков пространства, имеющих одинаковую длину, лежащих на параллельных прямых и одинаково направленных.

Если a, b - два вектора, то их суммой является тот класс эквивалентности d, содержащий направленный отрезок , который определяется по правилу параллелограмма по любому представителю из a и представителю с началом в точке A. Это определение сложения векторов корректно и не зависит от выбора представителя из a.

8. Упорядочение

Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементов   и   имеет место   или  .

Важнейший частный случай линейно упорядоченных множеств ― вполне упорядоченные множества.

Упорядоченное множество — множество с заданным отношением порядка.

Упорядоченные и частично упорядоченные множества(математичексие), множества, в которых каким-либо способом установлен порядок следования их элементов или, соответственно, частичный порядок. Понятия порядка и частичного порядка следования элементов определяются следующим образом. Говорят, что для пары элементов х, у множества М установлен порядок, если указано, который из этих элементов следует за другим (если у следует за хили, что то же самое, х предшествует у, то пишут х ?у, у ?х). Говорят, что в множестве М установлен частичный порядок следования элементов, если для некоторых пар его элементов установлен порядок, причём выполнены следующие условия: 1) никакой элемент не следует сам за собой; 2) если х ?у и у ?z,то х ?z (транзитивность отношения порядка). Может случиться, что в частично упорядоченном множестве М порядок не установлен ни для какой пары элементов М. С др. стороны, может случиться, что порядок установлен для всех пар различных элементов М, в этом случае частичный порядок следования элементов, установленный в множестве М, называют просто порядком следования элементов, или линейным порядком (упорядоченные множества, таким образом, являются видом частично упорядоченных множеств). Например, будем считать, что комплексное число a? + b?i следует за комплексным числом и а + bi, если a? > a и b? > b. Любое множество комплексных чисел становится тогда частично упорядоченным. В частности, частично упорядоченным становится любое множество действительных чисел (рассматриваемых как специальный случай комплексных). Т. к. при этом порядок следования таков, что действительное число a? следует за действительным числом а тогда и только тогда, когда a? больше а, то всякое множество действительных чисел оказывается даже просто упорядоченным. Понятия частично упорядоченного (иначе = полуупорядоченного) и упорядоченного множества принадлежат к числу основных общих понятий математики (см. Множеств теория), Вполне упорядоченные множества. Упорядоченное множество называется вполне упорядоченным, если каждое его подмножество обладает первым элементом (т. е. элементом, за которым следуют все остальные). Все конечные упорядоченные множества вполне упорядочены. Натуральный ряд, упорядоченный по возрастанию (а также некоторыми др. способами), образует вполне упорядоченное множество. Важность вполне упорядоченных множеств определяется главным образом тем, что для них справедлив принцип трансфинитной индукции (см. Трансфинитные числа). Упорядоченные множества, имеющие одинаковый порядковый тип, обладают и одинаковой мощностью, так что можно говорить о мощности данного порядкового типа. С др. стороны, конечные упорядоченные множества одинаковой мощности имеют один и тот же порядковый тип, так что каждой конечной мощности соответствует определённый конечный порядковый тип. Положение меняется при переходе к бесконечным множествам. Два бесконечных упорядоченных множества могут иметь одну и ту же мощность, но разные порядковые типы. Направленные множества. Частично упорядоченное множество называется направленным, если для всяких его элементов х и у существует такой элемент z, что z ?х и z ?у (a ?b означает, что либо a ?b, либо а = b). Понятие направленного множества позволяет дать весьма общее определение предела. Пусть f (p) - числовая (для простоты) функция, заданная на направленном множестве М; число с называется пределом f (p) по направленному множеству М, если для всякого e > 0 найдётся такой элемент , что для всех p из М таких, что р ³ р выполняется неравенство . Это определение позволяет установить все обычные свойства предела и охватывает весьма широкий класс частных случаев. Историческая справка. Теорию упорядоченных множеств создал Г. Кантор. В 1883 он ввёл понятие вполне упорядоченного множества и порядкового числа, а в 1895 = понятие упорядоченного множества и порядкового типа. В 1906=07 С. О. Шатуновский сформулировал определения направленного множества (у Шатуновского = расположенный комплекс) и предела по направленному множеству (амер. математиками Э. Г. Муром и Г. Л. Смитом эти же понятия были рассмотрены независимо от Шатуновского, но значительно позднее = в 1922). Общее понятие частично упорядоченного множества принадлежит Ф. Хаусдорфу (1914).  Лит.: Александров П. С., Введение в общую теорию множеств и функций, М. = Л., 1948; Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973; Хаусдорф Ф., Теория множеств, пер. с нем., М. = Л., 1937; Куратовский К., Мостовскиq А., Теория множеств, пер. с англ., М., 1970; Бурбаки Н., Теория множеств, пер. с франц., М., 1965.

9. Интервал упорядочного множества; связь с гиперкубом и картой карно.

Интервал И Сегмент

- простейшие множества точек на прямой. Интервалом (или промежутком) наз. множество точек прямой, заключенных между фиксированными точками Аи В, причем сами точки Аи Вне причисляются к интервалу. Сегментом (или отрезком) наз. множество точек прямой, лежащих между точками А и В, к к-рому присоединены и сами эти точки. Термины "интервал" и "сегмент" применяются также для обозначения соответствующих множеств действительных чисел: интервал состоит из чисел х, удовлетворяющих неравенствам а<x<b, a сегмент - из чисел х, удовлетворяющих неравенствам Интервал обозначается ( а, b), иногда ] а, b[, а сегмент [ а, b]. Термин "интервал" употребляется также в более широком смысле для обозначения произвольного связного множества на прямой. В этом случае к интервалам относятся собственно интервал ( а, b), бесконечные, или несобственные, интервалы (, ), сегмент [ а, b]и полуинтервалы [ а, b),( а, b], При этом круглая скобка обозначает, что соответствующий конец интервала не принадлежит к рассматриваемому множеству, а квадратная - что принадлежит. бсэ-з. Более общим является понятие интервала в частично упорядоченном множестве. Интервалом [ а, b]здесь наз. совокупность всех таких элементов хданного частично упорядоченного множества, к-рые удовлетворяют неравенству Интервал частично упорядоченного множества, состоящий в точности из двух элементов, наз. простым. Л. А. Скорняков.

10. Максимальный интервал. Задача упрощения Сднф и СКНФ

11. Лексико графический порядок

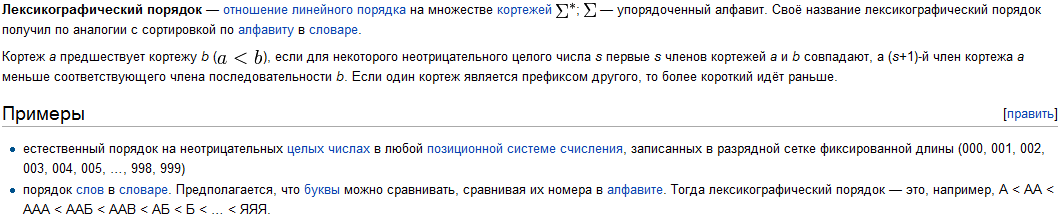
Реляционные базы данных.

1. Оснавные аспекты реляционных баз данных

Реляционная база данных — база данных, основанная на реляционной модели данных. Слово «реляционный» происходит от англ. relation (отношение^[1]). Для работы с реляционными БД применяют реляционные СУБД.

Реляционная база данных – описывает некоторые сущности или объекты и их свойства и записывают их в виде отношений.

Использование реляционных баз данных было предложено доктором Коддом из компании IBM в 1970 году.

Цели создания реляционной модели формулировались следующим образом.

• Обеспечение более высокой степени независимости от данных. Прикладные программы не должны зависеть от изменений внутреннего представления данных, в частности от изменений организации файлов, переупорядочивания записей и путей доступа.

• Создание прочного фундамента для решения семантических вопросов, а также проблем непротиворечивости и избыточности данных. В частности, в статье Кодда вводится понятие нормализованных отношений, т.е. отношений без повторяющихся групп.

• Расширение языков управления данными за счет включения операций над множествами.

2. Задачи реляционной субд.

Реляционная СУБД (РСУБД; иначе Система управления реляционными базами данных, СУРБД) — СУБД, управляющая реляционными базами данных.

Понятие реляционный (англ. relation — отношение) связано с разработками известного английского специалиста в области систем баз данных Эдгара Кодда (Edgar Codd).

Эти модели характеризуются простотой структуры данных, удобным для пользователя табличным представлением и возможностью использования формального аппарата алгебры отношений и реляционного исчисления для обработки данных.

Реляционная модель ориентирована на организацию данных в виде двумерных таблиц. Каждая реляционная таблица представляет собой двумерный массив и обладает следующими свойствами:

• каждый элемент таблицы — один элемент данных

• все ячейки в столбце таблицы однородные, то есть все элементы в столбце имеют одинаковый тип (числовой, символьный и т. д.)

• каждый столбец имеет уникальное имя

• одинаковые строки в таблице отсутствуют

• порядок следования строк и столбцов может быть произвольным

Базовыми понятиями реляционных СУБД являются:

• атрибут

• отношение

• кортеж

Отношение — фундаментальное понятие реляционной модели данных. По этой причине модель и называется реляционной (от лат. relatio — отношение, связь).

В математике корте́ж или  -ка (упорядоченная  -ка) — упорядоченный конечный набор длины   (где   — любое натуральное число либо 0), каждый из элементов которого   принадлежит некоторому множеству  ,  . Элементы кортежа могут повторяться в нём любое число раз (этим, в частности, он отличается от упорядоченного множества, куда каждый элемент может входить только в одном экземпляре).

3. Структура отношений: имя атрибута – имя домена.

Отношение. Плоская таблица, состоящая из столбцов и строк.

В любой реляционной СУБД предполагается, что пользователь воспринимает базу данных как набор таблиц. Однако следует подчеркнуть, что это восприятие относится только к логической структуре базы данных, т.е. к внешнему и к концептуальному уровням архитектуры ANSI-SPARC. Подобное восприятие не относится к физической структуре базы данных, которая может быть реализована с помощью различных структур хранения.

Атрибут. Именованный столбец отношения.

В реляционной модели отношения используются для хранения информации об объектах, представленных в базе данных. Отношение обычно имеет вид двумерной таблицы, в которой строки соответствуют отдельным записям, а столбцы — атрибутам. При этом атрибуты могут располагаться в любом порядке — независимо от их переупорядочииания отношение будет оставаться одним и тем же, а потому иметь тот же смысл.

Например, информация об отделениях компании может быть представлена отношением Branch, включающим столбцы с атрибутами faranchNo (Номер отделения), street (Улица), city (Город) и postcode (Почтовый индекс). Информация о работниках компании может быть представлена отношением Staff (Персонал), включающим столбцы с атрибутами staffNo (Табельный номер сотрудника), fName (Имя), IName (Фамилия), position (Должность), sex (Пол), DOB (Дата рождения), salary (Зарплата), branchNo (Номер отделения). На рисунке показаны примеры отношений Branch и Staff. Как видно из этого примера, каждый столбец содержит значения одного и того же атрибута — например, столбец branchNo содержит только номера существующих отделений компании.

Домен. Набор допустимых значений одного или нескольких атрибутов.

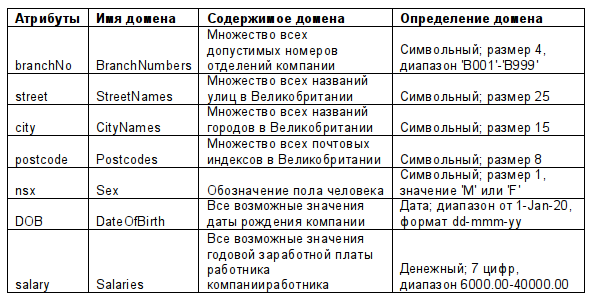
Домены представляют собой чрезвычайно мощный компонент реляционной модели. Каждый атрибут реляционной базы данных определяется на некотором домене. Домены могут отличаться для каждого из атрибутов, но два и более атрибутов могут определяться на одном и том же домене. В таблице представлены домены для некоторых атрибутов отношений Branch и Staff. Обратите внимание, что в любой момент времени в доменах могут существовать значения, которые реально не представлены значениями соответствующего атрибута. Понятие домена имеет большое значение, поскольку благодаря нему пользователь может централизованно определять смысл и источник значений, которые могут получать атрибуты. В результате при выполнении реляционной операции системе доступно больше информации, что позволяет избежать в ней семантически некорректных операций. Например, бессмысленно сравнивать название улицы с номером телефона, даже если для обоих этих атрибутов определениями доменов являются символьные строки. С другой стороны, помесячная арендная плата объекта недвижимости и количество месяцев, в течение которых он сдавался в аренду, принадлежат разным доменам (первый атрибут имеет денежный тип, а второй — целочисленный). Однако умножение значений из этих доменов является допустимой операцией. Как следует из этих двух примеров, обеспечить полную реализацию понятия домена совсем непросто, поэтому во многих реляционных СУБД они поддерживаются не полностью, а лишь частично.

Кортеж. Строка отношения.

Элементами отношения являются кортежи, или строки, таблицы. В отношении Branch каждая строка содержит семь значений, по одному для каждого атрибута. Кортежи могут располагаться в любом порядке, при этом отношение будет оставаться тем же самым, а значит, и иметь тот же смысл.

Описание структуры отношения вместе со спецификацией доменов и любыми другими ограничениями возможных значений атрибутов иногда называют его заголовком (или содержанием (intension)). Обычно оно является фиксированным, до тех пор, пока смысл отношения не изменится за счет добавления в него дополнительных атрибутов. Кортежи называются расширением (extension), состоянием (state) или телом отношения, которое со временем изменяется.

Степень. Степень отношения определяется количеством атрибутов, которое оно содержит.

Отношение Branch, показанное на рисунке, имеет четыре атрибута, и, следовательно, его степень равна четырем. Это значит, что каждая строка таблицы является четырехэлементным кортежем, т.е. кортежем, содержащим четыре значения. Отношение только с одним атрибутом имеет степень 1 и называется унарным (unary) отношением (дара одноэлементным кортежем). Отношение с двумя атрибутами называется бинарным (binary), отношение с тремя атрибутами — тернарным (ternary), а для отношений с большим количеством атрибутов используется термин п-арное (п-агу). Определение степени отношения является частью заголовка отношения.

Кардинальность. Количество кортежей, которое содержится в отношении.

Количество содержащихся в отношении кортежей называется кардинальностью отношения. Эта характеристика меняется при каждом добавлении или удалении кортежей. Кардинальность является свойством тела отношения и определяется текущим состоянием отношения в произвольно взятый момент. И наконец, мы подошли к определению самой реляционной базы данных.

Реляционная база данных. Набор нормализованных отношений, которые различаются по именам.

Реляционная база данных состоит из отношений, структура которых определяется с помощью особых методов, называемых нормализацией (normalization).

4.функциональные зависимости.

Реляционная база данных содержит как структурную, так и семантическую информацию. Структура базы данных определяется числом и видом включенных в нее отношений, и связями типа "один ко многим", существующими между кортежами этих отношений. Семантическая часть описывает множество функциональных зависимостей, существующих между атрибутами этих отношений. Дадим определение функциональной зависимости.

Определение:

Если даны два атрибута X и Y некоторого отношения, то говорят, что Y функционально зависит от X, если в любой момент времени каждому значению X соответствует ровно одно значение Y.

Функциональная зависимость обозначается X -> Y. Отметим, что X и Y могут представлять собой не только единичные атрибуты, но и группы, составленные из нескольких атрибутов одного отношения.

Можно сказать, что функциональные зависимости представляют собой связи типа "один ко многим", существующие внутри отношения.

Некоторые функциональные зависимости могут быть нежелательны.

Определение:

Избыточная функциональная зависимость - зависимость, заключающая в себе такую информацию, которая может быть получена на основе других зависимостей, имеющихся в базе данных.

Корректной считается такая схема базы данных, в которой отсутствуют избыточные функциональные зависимости. В противном случае приходится прибегать к процедуре декомпозиции (разложения) имеющегося множества отношений. При этом порождаемое множество содержит большее число отношений, которые являются проекциями отношений исходного множества. (Операция проекции описана в разделе, посвященном реляционной алгебре). Обратимый пошаговый процесс замены данной совокупности отношений другой схемой с устранением избыточных функциональных зависимостей называется нормализацией.

Условие обратимости требует, чтобы декомпозиция сохраняла эквивалентность схем при замене одной схемы на другую, т.е. в результирующих отношениях:

• не должны появляться ранее отсутствовавшие кортежи;

• на отношениях новой схемы должно выполняться исходное множество функциональных зависимостей.

5. Теоретико множественные операции и иные операции над отношениями.

Напомним, что

алгеброй - называется множество объектов с заданной на нем совокупностью операции, замкнутых относительно этого множества, называемого основным множеством.

Основное множество в реляционной алгебре - это всё возможное множество отношений.

Всего Э. Ф. Коддом было предложено 8 операций для реляционной алгебры. В общем это множество избыточное, так как одни операции могут быть представлены через другие, однако множество операций выбрано из соображений максимального удобства при реализации произвольных запросов к БД. Все множество операций можно разделить на две группы: теоретико-множественные операции и специальные операции. В первую группу входят 4 операции. Три первые теоретико-множественные операции являются бинарными, то есть в них участвуют два отношения и они требуют эквивалентных схем исходных отношений.

Объединение двух отношений - это отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно.

Пусть заданы два отношения R₁ = { r₁ } , R₂ = { r₂ }. где r₁ и r₂ — соответственно кортежи отношений R₁ и R₂, то объединение

R₁ R₂ = { г | г R₁ r R₂ }. Здесь r — кортеж нового отношения, — операция логического сложения «ИЛИ».

Пример применения операции объединения приведен на рис. 4.1. Исходными отношениями являются отношения R₁ и R₂, которые содержат перечни деталей. изготавливаемых соответственно на первом и втором участках цеха. Отношение R₃ содержит общин перечень деталей, изготавливаемых в цеху, то есть характеризует общую номенклатуру цеха.

R1
Шифр детали	Название детали
00011073	Гаика Ml
00011075	Гайка М2
00011076	Гаика M3
00011003	Болт Ml
00011006	Болт МЗ
00013063	Шайба Ml
00013066	Шайба МЗ

 

R2
Шифр детали	Название детали
00011073	Гайка М1
00011076	Гайка М3
00011077	Гайка М4
00011004	Гайка М2
00011006	Гайка М3

 

R3
Шифр детали	Название детали
00011073	Гайка Ml
00011075	Гайка М2
00011076	Гайка МЗ
00011003	Болт Ml
00011006	Болт МЗ
00013063	Шайба Ml
00013066	Шайба МЗ
00011077	Гайка М4
00011004	Болт М2

Пересечение отношений в реляционной алгебре - это отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям. R₁ и R₂:

R₃ = R₁  R₂={ г | r R₁ ^ г R₂ }, здесь ^ - операция логического умножения (логическое «И»).

В отношении R₄ содержатся перечень деталей, которые выпускаются одновременно на двух участках цеха.

R4
Шифр детали	Название детали
00011073	Гайка Ml
00011076	Гайка МЗ
00011006	Болт МЗ

Разность отношений в реляционной алгебре - это отношение R₁ и R₂, содержащее множество кортежей, принадлежащих R₁ и не принадлежащих R₂:

R₅ = RI \ R₂ = { r | r R₁ ^ r R₂ }

Отношение R₅ содержит перечень деталей, изготавливаемых только на участке 1, отношение R_G содержит перечень деталей, изготавливаемых только на участке 2.

R₆ = R₂ \ R₁ = { r | r R₂ ^ rR₁ }

R5
Шифр детали	Название детали
00011075	Гайка М2
00011003	Болт Ml
00013063	Шайба Ml
00013066	Шайба МЗ

 

R6
Шифр детали	Название детали
00011077	Гайка М4
00011004	Болт М2

Следует отметить, что первые две операции, объединение и пересечение, являются коммутативными операциями, то есть результат операции не зависит от порядка аргументов в операции. Операция же разности является принципиально несимметричной операцией, то есть результат операции будет различным для разного порядка аргументов, что и видно из сравнения отношений R₅ и R₆.

В отличие от навигационных средств манипулирования данными в теоретико-графовых моделях операции реляционной алгебры позволяют получить сразу иной качественный результат, который является семантически гораздо более ценным и понятным пользователям. Например, сравнение результатов объединения и разности номенклатуры двух участков позволит оценить специфику производства: насколько оно уникально на каждом участке, и, в зависимости от необходимости, принять соответствующее решение по изменению номенклатуры.

Для демонстрации возможностей трех первых операций реляционной алгебры рассмотрим еще один пример — уже из другой предметной области. Исходными являются три отношения R₁ R₂ и R₃. Все они имеют эквивалентные схемы.

• R₁= (ФИО, Паспорт, Школа);

• R₂= (ФИО, Паспорт, Школа);

• R₃= (ФИО, Паспорт, Школа).

Рассмотрим ситуацию поступления в высшие учебные заведения, которая была характерна для периода, когда были разрешены так называемые репетиционные вступительные экзамены, которые сдавались раньше основных вступительных экзаменов в вуз. Отношение R₁ содержит список абитуриентов, сдававших репетиционные экзамены. Отношение, R₂ содержит список абитуриентов, сдававших экзамены на общих условиях. И наконец, отношение R₃ содержит список абитуриентов, принятых в институт. Будем считать, что при неудачной сдаче репетиционных экзаменов абитуриент мог делать вторую попытку и сдавать экзамены в общем потоке, поэтому некоторые абитуриенты могут присутствовать как в первом, так и во втором отношении.

Ответим на следующие вопросы:

1. Список абитуриентов, которые поступали два раза и не поступили в вуз. R = R₁  R₂ \ R₃

2. Список абитуриентов, которые поступили в вуз с первого раза, то есть они сдавали экзамены только один раз и сдали их так хорошо, что сразу были зачислены в вуз. R = (R₁ \ R₂   R₃ ) (R₂ \ R₁  R₃)

3. Список абитуриентов, которые поступили в вуз только со второго раза.

Прежде всего это те абитуриенты, которые присутствуют в отношениях R₁ и R₂, потому что они поступали два раза, и присутствуют в отношении R₃, потому что они поступили. R = R₁   R₂   R₃

4. Список абитуриентов, которые поступали только один раз и не поступили.

Это прежде всего те абитуриенты; которые присутствуют в R₁ и не присутствуют в R₂, и те, кто присутствуют в R₂ и не присутствуют в R₁. И разумеется, никто из них не присутствует в R₃. R = (R₁ \ R₂)  (R₂ \ R₁) \ R₃ 

В отсутствие скобок порядок выполнения операций реляционной алгебры естественный, поэтому сначала будут выполнены операции в скобках, а затем будет выполнена последняя операция вычитания отношения R₃.

Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами.

Кроме перечисленных трех теоретико-множественных операций в рамках реляционной алгебры определена еще одна теоретико-множественная операция — расширенное декартово произведение. Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция расширенного декартова произведения, обозначаемая R₁ ® R₂, допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.

Сцеплением, пли конкатенацией, кортежей с = <c₁, с₂, ..., с_n> и q = <q₁, q₂, ..., q_m> называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей с и q обозначается как (с , q).

(с, q) = <с₁ с₂, ... , с_n, q₁, q₂, .... q_m>

Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q.

Все предыдущие операции не меняли степени или арности отношений — это следует из определения эквивалентности схем отношений. Операция декартова произведения меняет степень результирующего отношения.

Расширенным декартовым произведением отношения R, степени n со схемой

S_R1=(А₁,А₂...,А_n) и отношения R₂ степени m со схемой

S_R2=(В₁,В₂, ... , В_m) называется отношение R₃ степени n+m со схемой

S_R3 = (А₁, А₂, ... , А_n, В₁, В₂, ..., В_m),

содержащее кортежи, полученные сцеплением каждого кортежа г отношения R] с каждым кортежем q отношения R₂.

То есть если R₁ = { r }, R₂ = { q }

R₁ R₂ = {(r, q) | r R₁ ^ q R₂}

Операцию декартова произведения с учетом возможности перестановки атрибутов в отношении можно считать симметричной. Очень часто операция расширенного декартова произведения используется для получения некоторого универсума — т. е. отношения, которое характеризует все возможные комбинации между элементами отдельных множеств. Однако самостоятельного значения результат выполнения операции обычно не имеет, он участвует в дальнейшей обработке. Например, на производстве в отношении 07 задана обязательная номенклатура деталей для всех цехов, а в отношении 08 дан перечень всех цехов.

R7
Шифр детали	Название детали
00011073	Гайка M1
00011075	Гайка М2
00011076	Гайка МЗ
00011003	Болт М1
00011006	Болт МЗ
00013063	Шайба Ml
00013066	Шайба МЗ
00011077	Гайка М4
000ll004	Болт М2
00011005	Болт М5
00011006	Болт М6
00013062	Шайба М2

 

R8

Цех

Цех 1

Цех 2

Цех 3

Тогда отношение R₉, которое соответствует ситуации, когда каждый цех изготавливает все требуемые детали, будет выглядеть следующим образом:

R9
Шифр детали	Название детали	Цех
00011073	Гайка Ml	Цех 1
00011075	Гайка М2	Цех 1
00011076	Гайка МЗ	Цех 1
00011003	Болт Ml	Цех 1
00011006	Болт МЗ	Цех 1
00013063	Шайба Ml	Цех 1
00013066	Шайба МЗ	Цех 1
00011077	Гайка М4	Цех 1
00011004	Болт М2	Цех 1
00011005	Болт М5	Цех 1
00011006	Болт Мб	Цех 1
00013062	Шайба М2	Цех 1
00011073	Гайка Ml	Цех 2
00011075	Ганка М2	Цех 2

 

R10
Шифр	Название детали	Цех
00011073	Гайка Ml	Цех 1
(МО И 075 000 11 076	Гайка М2 Гайка МЗ	Цех 1 Цех 1
000 11 003	! Болт Ml	Цех 1
0011 0006	Болт МЗ	Цех 1
00013063	Шайба Ml	Цех 1
000 11060	Шайба МЗ	Цех 1
000 11 004	Болт М2	Цех 1
00011077	Гайка М4	Цех 1
00011006	Болт МЗ	Цех2
00013063	Шайба Ml	Цех 2
0013066	Шайба МЗ	Цех 2
00011077	Гайка М4	Цех 2
0001 0778	Болт М2	Цех 2

 

00011076	Гайка МЗ	Цех 2
00011U03	Болт Ml	Цех 2
00011006	Болт МЗ	Цех 2
00013063	Шайба Ml	Цех 2
00013066	Шайба МЗ	Цех 2
00011077	Гайка М4	Цех 2
00011004	Болт М'2	Цех 2
00011005	Болт М5	Цех 2
00011006	Болт Мб	Цех 2
00013062	Шайба М2	Цех 2
00011073	Гайка Ml	ЦсхЗ
00011075	Гайка М2	ЦехЗ
00011076	Гайка МЗ	Цех 3
00011003	Болт Ml	ЦехЗ
00011006	Болт МЗ	ЦехЗ
00013063	Шайба Ml	Цех 3
00013066	Шайба МЗ	ЦехЗ
00011077	Гайка М4	ЦехЗ
00011004	Болт М2	Цех 3
00011005	Болт М5	ЦехЗ
00011006	Болт Мб	ЦехЗ
00013062	Шайба М2	ЦехЗ

 

00011006	Болт Мб	Цех 2
00013062	Шайба М2	Цех 2
00011073	Гайка Ml	ЦeхЗ
00011075	Гайка М2	ЦехЗ
00011076	Гайка МЗ	ЦехЗ
00011003	Болт Ml	ЦехЗ
00011006	Болт МЗ	Цех 3
00013063	Шайба Ml	Цех 3
00013066	Шайба МЗ	ЦехЗ
00011077	Гайка М4	Цeх3
00011005	Болт М5	Цех3
00011006	Болт Мб	Цех3
00011005	Болт М5	Цех 1
00011006	Болт Мб	Цех 1
00013062	Шайба М2	Цех1

В каких запросах нужно использовать расширенное декартово произведение? Эта операция моделирует некоторую ситуацию, которая характеризуется словом «все». Поэтому если нам надо узнать, какие детали в каких цехах из общей обязательной номенклатуры не выпускаются, то мы можем вычесть из полученного отношения R₉ отношение R₁₀, характеризующее реальный выпуск деталей в каждом цехе.

Отношение R₁₁, которое является результатом выполнения этой операции, имеет вид:

R₁₁ ⁼ R₉ \ R₁₀

R11
Шифр детали	Название детали	Цех
00011073	Гайка Ml	Цех 2
00011075	Гайка М2	Цех 2
00011076	Гайка МЗ	Цех 2
00011004	Болт М2	ЦехЗ
00013062	Шайба М2	ЦехЗ
00011003	Болт Ml	Цех 2
00011005	Болт М5	ЦехЗ

Группа теоретико-множественных операций избыточна, так, например, операцию можно заменить сочетанием операций объединения и пересечения.

(R₁  R₂) \ (R₁ \ R₂) \ (R₂ \ R₁)

Однако это достаточно сложная формула, и именно поэтому все три теоретико-множественные операции вошли в базовый набор операций реляционной алгебры.

Далее мы переходим к группе операций, названных специальными операциями реляционной алгебры.

6. Основные понятия ER: сущность – объект, атрибут – характеристика объекта. Мощность связи – один к одному, один ко многим или многие ко многим. Модальность связи – обязательная или необязательная.

10.2. Семантическая модель Entity-Relationship (Сущность-Связь)

В этой лекции мы кратко рассмотрим некоторые черты одной из наиболее популярных семантических моделей данных – модели «Сущность-Связь» (часто ее называют кратко ER-моделью от Entity-Relationship).

Здесь следует сделать два замечания, касающиеся, главным образом, терминологии. Оба термина relationи relationship могут быть переведены на русский язык как отношение. Поэтому в русскоязычной литературе ER-модель иногда называют моделью сущность-отношение, а иногда и реляционной семантической моделью. Наверное, в этом нет ничего страшного, если говорить о ER-модели в отрыве от тематики проектирования реляционных баз данных.

Но если требуется одновременно использовать термины ER-модели и реляционной модели данных, то, безусловно, требуется применять для терминов relation и relationship разные русские эквиваленты. За этими терминами стоят весьма различные понятия. В реляционной модели отношение (relation) – это единственная родовая структура данных. С помощью этого же механизма представляются «связанные» сущности (вспомните, например, про внешние ключи). Как мы увидим немного позже, в ER-модели для представления схемы базы данных используются два равноправных понятия – сущность и связь. Связи в ER-модели играют роль, отличную от той, какую играют отношения в реляционной модели данных.

Кроме того, в русскоязычную терминологию вошла и чистая транслитерация термина relation именно в смысле отношение. Мы говорим, например, про реляционную модель данных, реляционную алгебру и т. д., понимая модель данных, основанную на отношениях, алгебру отношений и т. п. По этому поводу, по крайней мере, в контексте баз данных, разумно окончательно зарезервировать термины relation иотношение для обозначения понятий реляционной модели данных, а для термина relationshipиспользовать другой допустимый русскоязычный эквивалент – связь.

На использовании разных вариантов ER-модели основано большинство современных подходов к проектированию баз данных (главным образом, реляционных). Модель была предложена Питером Ченом (Peter Chen) в 1976 г. Моделирование предметной области базируется на использовании графических диаграмм, включающих небольшое число разнородных компонентов. Простота и наглядность представления концептуальных схем баз данных в ER-модели привели к ее широкому распространению в CASE-системах, поддерживающих автоматизированное проектирование реляционных баз данных. Среди множества разновидностей ER-моделей одна из наиболее популярных и развитых применялась в системе CASE компании Oracle. Мы обсудим некоторый упрощенный вариант этой модели. Если говорить более точно, сосредоточимся на ее структурной и целостной частях.

10.2.1. Основные понятия er-модели

Основными понятиями ER-модели являются сущность, связь и атрибут. Сущность – это реальный или представляемый объект, информация о котором должна сохраняться и быть доступной.⁴³⁾ В диаграммах ER-модели  сущность представляется в виде прямоугольника, содержащего имя сущности. При этом имя сущности – это имя типа, а не некоторого конкретного экземпляра этого типа.⁴⁴⁾ Для большей выразительности и лучшего понимания имя сущности может сопровождаться примерами конкретных экземпляров этого типа.

  Рис. 10.1.  Пример типа сущности

На рис. 10.1 изображена сущность  АЭРОПОРТ с примерными экземплярами «Шереметьево» и «Хитроу». Эта примитивная диаграмма тем не менее несет важную информацию. Во-первых, она показывает, что в базе данных будут содержаться однотипные структуры данных (экземпляры сущности), описывающие аэропорты. Во-вторых, поскольку в жизни существует несколько точек зрения на аэропорты (например, точка зрения пилота, точка зрения пассажира, точка зрения администратора) и этим точкам зрения соответствуют разные структуры данных, то приведенные примеры аэропортов позволяют несколько сузить допустимый набор точек зрения. В нашем случае приведены примеры международных аэропортов, так что, скорее всего, имеется точка зрения пассажира или пилота международных авиарейсов.

При определении типа сущности необходимо гарантировать, что каждый экземпляр сущности может быть отличим от любого другого экземпляра той же сущности. Это требование в некотором роде аналогично требованию отсутствия кортежей-дубликатов в реляционных таблицах.

Связь – это графически изображаемая ассоциация, устанавливаемая между двумя типами сущностей. Как и сущность, связь – это типовое понятие, все экземпляры обоих связываемых типов сущностей подчиняются устанавливаемым правилам связывания. Поэтому правильнее говорить о типе связи, устанавливаемой между типами сущности, и об экземплярах типа связи, устанавливаемых между экземплярами типа сущности.⁴⁵⁾ В обсуждаемом здесь варианте ER-модели эта ассоциация всегда является бинарной и может существовать между двумя разными типами сущностей или между типом сущности и им же самим (рекурсивная связь). В любой связи выделяются два конца (в соответствии с существующей парой связываемых сущностей), на каждом из которых указываются имя конца связи, степень конца связи (сколько экземпляров данного типа сущности должно присутствовать в каждом экземпляре данного типа связи), обязательность связи (т. е. любой ли экземпляр данного типа сущности должен участвовать в некотором экземпляре данного типа связи).⁴⁶⁾

Связь представляется в виде ненаправленной линии, соединяющей две сущности или ведущей от сущности к ней же самой. При этом в месте «стыковки» связи с сущностью используются:

• трехточечный вход в прямоугольник сущности, если для этой сущности в связи могут (или должны) использоваться много (many) экземпляров сущности;

• одноточечный вход, если в связи может (или должен) участвовать только один экземпляр сущности.

Обязательный конец связи изображается сплошной линией, а необязательный – прерывистой линией.

Связь между сущностями  БИЛЕТ и ПАССАЖИР, показанная на рис. 10.2, связывает билеты и пассажиров. Конец связи с именем «для» позволяет связывать с одним пассажиром более одного билета, причем каждый билет должен быть связан с каким-либо пассажиром. Конец связи с именем «имеет» показывает, что каждый билет может принадлежать только одному пассажиру, причем пассажир не обязан иметь хотя бы один билет.

  Рис. 10.2.  Пример типа связи

Лаконичная устная трактовка изображенной диаграммы состоит в следующем:

• каждый БИЛЕТ предназначен для одного и только одного ПАССАЖИРА;

• каждый ПАССАЖИР может иметь один или более БИЛЕТОВ.

На следующем примере (рис. 10.3) изображена рекурсивная связь, связывающая сущность  МУЖЧИНА с ней же самой. Конец связи с именем «сын» определяет тот факт, что несколько людей могут быть сыновьями одного отца. Конец связи с именем «отец» означает, что не у каждого мужчины должны быть сыновья.

  Рис. 10.3.  Пример рекурсивного типа связи

Лаконичная устная трактовка изображенной диаграммы состоит в следующем:

• каждый МУЖЧИНА является сыном одного и только одного МУЖЧИНЫ;

• каждый МУЖЧИНА может являться отцом одного или более МУЖЧИН.

Атрибутом сущности является любая деталь, которая служит для уточнения, идентификации, классификации, числовой характеристики или выражения состояния сущности. Имена атрибутов заносятся в прямоугольник, изображающий сущность, под именем сущности и изображаются малыми буквами, возможно, с примерами.

Пример типа сущности  ЧЕЛОВЕК с указанными атрибутами показан на рис. 10.4. С технической точки зрения атрибуты  типа сущности в ER-модели похожи на атрибуты отношения в реляционной модели данных. И в том, и в другом случаях введение именованных атрибутов вводит некоторую типовую структуру данных, имя которой совпадает с именем типа сущности в случае ER-модели или с именем переменной отношения в случае реляционной модели. Этой типовой структуре должны следовать все экземпляры типа сущности или все кортежи отношения. Но имеется и важное отличие. Напомним, что в реляционной модели данных атрибут определяется как упорядоченная пара <имя_атрибута, имя_домена>(или <имя_атрибута, имя_базового_типа_данных>, если понятие домена не поддерживается). Заголовок отношения, определяемый как множество таких пар, представляет собой полный аналог структурного типа данных в языках программирования.

  Рис. 10.4.  Пример типа сущности с атрибутами

При определении атрибутов типа сущности в ER-модели указание домена атрибута не является обязательным, хотя это и возможно (см. ниже). Обсудим, чем вызвана эта возможность «ослабленного» определения атрибутов. Прежде всего, как отмечалось в разделе 10.1 Введение, семантические модели данных используются для построения концептуальных схем БД, и эти схемы преобразуются в реляционные схемы БД, которые поддерживаются той или иной СУБД. Несмотря на то, что в настоящее время типовые возможности РСУБД в основном стандартизованы (на основе стандарта языка SQL), детали базового набора типов данных и средств определения доменов в разных системах могут различаться. Поскольку производители CASE-средств проектирования реляционных БД стремятся не связывать обеспечиваемые ими возможности семантического моделирования с конкретной реализацией СУБД, они стимулируют откладывание строгого определения типов атрибутов до стадии полного определения реляционной схемы.

Кроме того, напомним, что при определении атрибута отношения допускается использование имен атрибутов, совпадающих с именами своих доменов (это два разных пространства имен, и наличие одинаковых имен у атрибутов и доменов не вызывает коллизий). Поэтому при определении атрибутов типов сущности можно так подбирать их имена, что они в дальнейшем будут подсказывать, какие домены у этих атрибутов имеются в виду. Пониманию предполагаемой сути доменов способствует и возможность указания примеров значений атрибутов. Например, на рис. 10.4 имеется атрибут  год рождения, в качестве примерного значения которого указано «1976». Это подсказывает, что в реляционной схеме при определении соответствующего атрибута наиболее естественным базовым типом данных будет темпоральный тип «ДАТА», значения которого задают дату с точностью до года.