10.2.2. Уникальные идентификаторы типов сущности

Как отмечалось выше, при определении типа сущности необходимо гарантировать, что каждый экземпляр сущности является отличимым от любого другого экземпляра той же сущности. Поскольку сущность является абстракцией реального или представляемого объекта внешнего мира, это требование нужно иметь в виду уже при выборе кандидата в типы сущности. Например, предположим, что проектируется база данных для поддержки работы книжного склада. На складе могут храниться произвольные части тиража любого издания любой книги. Может ли в этом случае индивидуальная книга являться прообразом типа сущности? Утверждается, что нет, поскольку отсутствует возможность различения книг одного издания. Для книжного склада прообразом типа сущности будет набор одноименных книг одного автора, вышедших в одном издании. Одним из атрибутов этого типа сущности будет число книг в наборе. Но когда книга поступает в библиотеку и ей присваивается уникальный библиотечный номер, она становится разумным прообразом типа сущности. Плохо устроены библиотеки, в которых не различаются индивидуальные книги (даже одноименные книги одного автора, вышедшие в одном издании).

Но при проектировании базы данных мало того, чтобы проектировщик убедился в правильном выборе типов сущности, гарантирующем различие экземпляров каждого типа сущности. Необходимо сообщить системе автоматизации проектирования БД, каким образом будут различаться эти экземпляры, т. е. сообщить, как конструируются уникальные идентификаторы  экземпляров каждого типа сущности. В ER-модели у экземпляра типа сущности не может быть назначаемого пользователем имени или назначаемого системой внешнего уникального идентификатора. Экземпляр типа сущности может идентифицироваться только своими индивидуальными характеристиками, а они представляются значениями атрибутов и экземплярами типов связи, связывающими данный экземпляр типа сущности с экземплярами других типов сущности или этого же типа сущности. Поэтому уникальным идентификатором сущности может быть атрибут, комбинация атрибутов, связь, комбинация связей или комбинация связей и атрибутов, уникально отличающая любой экземпляр сущности от других экземпляров сущности того же типа.

Приведем несколько примеров. На рис. 10.5 показан тип сущности  КНИГА, пригодный для использования в базе данных книжного склада. При издании любой книги в любом издательстве (кроме пиратских, которыми мы для простоты пренебрежем) ей присваивается уникальный номер – ISBN. Понятно, что значение атрибута  isbn будет уникально идентифицировать партию книг на складе. Кроме того, конечно, в качестве уникального идентификатора годится и комбинация атрибутов  <автор, название, номер издания, издательство, год издания>.

  Рис. 10.5.  Тип сущности, экземпляры которого идентифицируются атрибутами

На рис. 10.6 диаграмма включает два связанных типа сущности. У каждого взрослого человека имеется один и только один паспорт (мы снова не берем в расчет особый случай, когда у одного человека имеется несколько паспортов), и каждый паспорт может принадлежать только одному взрослому человеку (некоторые уже готовые паспорта могут быть еще никому не выданы). Тогда связь человека с его паспортом (конец связи  ИМЕЕТ) уникально идентифицирует взрослого человека, т. е., грубо говоря, паспорт определяет взрослого человека. Поскольку могут существовать паспорта, еще не выданные какому-либо человеку, эта связь не является уникальным идентификатором сущности  ПАСПОРТ.

  Рис. 10.6.  Тип сущности, экземпляры которого идентифицируются связью

На рис. 10.7 диаграмма включает три связанных типа сущности. Профессора обладают знаниями в нескольких учебных дисциплинах. Преподавание каждой дисциплины доступно нескольким профессорам. Другими словами, между сущностями  ПРОФЕССОР и ДИСЦИПЛИНА определена связь «многие ко многим». Каждый профессор может готовить курсы по любой доступной ему дисциплине. Каждой дисциплине может быть посвящено несколько учебных курсов. Но каждый профессор может готовить только один курс по любой доступной ему дисциплине, и каждый курс может быть посвящен только одной дисциплине. Тем самым, каждый экземпляр типа сущности  КУРС уникально идентифицируется экземпляром сущности  ПРОФЕССОР и экземпляром сущности  ДИСЦИПЛИНА, т. е. парой связей с именами концов  ГОТОВИТСЯ и ПОСВЯЩЕН на стороне сущности  КУРС. Заметим, что сущности  ПРОФЕССОР иДИСЦИПЛИНА  связями не идентифицируются.

  Рис. 10.7.  Тип сущности, экземпляры которого идентифицируются комбинацией связей

Наконец, на рис. 10.8 приведен пример типа сущности, уникальный идентификатор которого является комбинацией атрибутов и связей. Это несколько уточненный вариант сущности с рекурсивной связью срис. 10.3. У каждого человека могут быть дети, и у каждого человека имеется отец. Тогда, если предположить, что близнецам, появившимся на свет одновременно, не дают одинаковых имен, то уникальным идентификатором типа сущности  ЧЕЛОВЕК может быть комбинация атрибутов  <дата рождения, ФИО> и связь с именем конца  РЕБЕНОК.

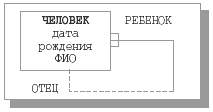  Рис. 10.8.  Тип сущности, экземпляры которого идентифицируются комбинацией атрибутов и связей

43   Понятно, что это «определение» на самом деле является тавтологией, поскольку, во-первых, мы пытаемся определить термин сущность через не определенный термин объект, а во-вторых, попытки определения термина объект настолько же безнадежны. Обычно авторы пытаются оправдываться тем, что в подобном контексте они имеют в виду «житейское», а не сколько-нибудь формализованное понятие объекта. Конечно, от этого не становится легче, поскольку понятие сущности должно пониматься в достаточно точном смысле. Но эта тавтология не изобретена автором этого курса; она традиционна для области семантического моделирования. В этой области стремятся максимально избегать формальностей.

44   Хотя было бы правильнее всегда использовать термины тип сущности и экземпляр типа сущности, для избежания многословности (и следуя традиции) в тех случаях, где это не приводит к двусмысленности, мы будем использовать термин сущность в значении типа сущности.

45   Тем не менее, как и в случае типа сущности, мы будем часто использовать термин связь в значении типа связи.

46   В некоторых вариантах ER-модели  конец связи называют ролью связи в данной сущности. Тогда можно говорить об имени роли, степени роли и обязательности роли связи в данной сущности.

7. Преобразование ER модели в структуру базы данных.

Графы.

1. Изображение графа. Предстовление графа (матрицы смежности, инцидентности)

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами.

2. Изоморфизм.

ГРАФОВ ИЗОМОРФИЗМ

- отношение эквивалентности на множестве графов. Изоморфным отображением одного неориентированного графа на другой наз. взаимно однозначное отображение вершин и ребер одного графа соответственно на вершиныи ребра другого графа, при к-ром сохраняется отношение инцидентности. Два графа наз. изоморфными, если существует изоморфное отображение одного из этих графов на другой. Графы G1 и G2, представленные на рис., не изоморфны, a G1 и G3 изоморфны. Обычно изоморфные графы не различают. Число попарно неизоморфных графов с данным числом вершин и данным числом ребер конечно. Подобным образом можно определить изоморфизм ориентированных графов, гиперграфов и сетей.

3. Клика.

Клика — полный подграф неориентированного графа. Другими словами, клика графа есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством.

4. Маршрут, путь, цепь, контур, цикл.

Маршрут – график чередующихся последовательных вершин дуг, где два соседних элемента инцидентны.

Путь – все ребра различны.

Цепь графа - это конечная или бесконечная последовательность ветвей графа, в которой каждые предыдущая и последующая ветви являются смежными.

 Контур -Замкнутый путь, образованный узлами и ветвями графа, в котором один из узлов является одновременно начальным и конечным узлом пути графа

Цикл – начальная и конечная вершины совпадают.

5.Эйлеров цикл (путь)

Эйлеров цикл – содержит все ребра графов по одному разу.

6. Гемильтонов цикл (путь)

Гамельтонов цикл – проходит через каждую вершину графа только единожды.

7. Алгоритм уоршила транзитивного замыкания

Рассмотрим еще один способ вычисления транзитивного замыкания диграфа. Пусть б будет диграфом из п узлов и т путей. Будем вычислять транзитивное замыкание диграфа серией циклов. Инициируем б₀ = б

и в произвольном порядке пронумеруем узлы в б как vi, V2, …, v_n. Затем вычисляем первый цикл. В общем случае на шаге к создается диграф б_к, начиная с б_к =6_к__{ и добавляя направленный путь (v/,vy), если диграфб_кА содержит оба пути   и (v^v_y). Таким образом, получаем простое

правило, выраженное приведенным ниже утверждением.

Утверждение 12.11. Для / = 1, …, п в диграфе G_k тогда и только тогда имеется путь (v,,vy), когда в диграфе существует направленный путь от v, до Vj, если расположенные между ними узлы (при наличии таковых) будут входить в множество {vi, v^}. В частности, G_n равен G\ транзитивному замыканию диграфа G.

Из утверждения 12.11 вытекает простой алгоритм вычисления транзитивного замыкания диграфа <5, в основу которого положена серия описанных выше циклов. Данный алгоритм получил известность как алгоритм Флойда-Уоршалла, и его псевдокод приведен во фрагменте кода 12.10. С помощью этого псевдокода легко проанализировать время выполнения алгоритма Флойда-Уоршалла, поскольку структура данных, представляющая G, поддерживает выполнение методов areAdjacent и insertDirectedEdge за 0(1) времени. Основной цикл выполняется п раз, а внутренний цикл обрабатывает каждую из 0(п²) пар узлов, выполняя для каждой пары вычислительные операции с постоянным временем. Таким образом, общее время выполнения алгоритма Флойда-Уоршалла составляет 0(я³).

Алгоритм FloydWarshall(G):