Задача о максимальном потоке

На практике часто возникает проблема определения максимальной проводимости некоторой реальной сети: сети транспортной, сети ЭВМ, других. Иногда нужно определить самый дешёвый поток и т.д. Все эти и многие другие задачи решаются с помощью алгоритмов, которые работают на сетях. Так, алгоритм о максимальном потоке ищет максимально возможную пропускную способность сети, алгоритм минимальной стоимости – самый дешёвый поток. В данном разделе будем рассматривать задачу о максимальном потоке.

Задача заключается в нахождении такого множества потоков по дугам, чтобы величина Q(v_s) была максимальной.

Разрез S отделяет v_s от v_t, если вершины v_s, v_t принадлежат разным сторонам разреза: v_s  V_s, v_t  V_t, V = V_s  V_t. Пропускной способностью с(S) разреза S называется сумма пропускных способностей дуг разреза, которые начинаются в V_s и заканчивается в V_t:

с(S) =

13. Префиксный код и его дерево.

Пре́фиксный код в теории кодирования — код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует. Хотя префиксный код состоит из слов разной длины, эти слова можно записывать без разделительного символа.

Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:

0 10 0 11 0 11 10

14. Код Хаффмана. Оптимальность кода Хаффмана.

15. Код Фано.

16. Создание бинарного дерева упорядочного множества. Удаление вершины.

Бинарное (двоичное) дерево (binary tree) - это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла. Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом. Схематичное изображение бинарного дерева: 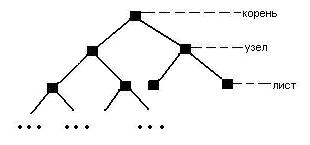Бинарное дерево может представлять собой пустое множество. Бинарное дерево может выродиться в список: Построение бинарного дерева Сначала мы должны определить структуру для создания корня и узлов дерева:

template<class T> struct TNode { T value; TNode *pleft, *pright; //constructor TNode() { pleft = pright = 0; } };

Здесь поля pleft и pright - это указатели на потомков данного узла, а поле value предназначено для хранения информации. Теперь мы можем написать рекурсивную функцию, которая будет вызываться при создании дерева:

template<class T> void makeTree(TNode<T>** pp, T x) { if(!(*pp)) { TNode<T>* p = new TNode<T>(); p->value = x; *pp = p; } else { if((*pp)->value > x) makeTree(&((*pp)->pleft), x); else makeTree(&((*pp)->pright), x); } }

Эта функция добавляет элемент x к дереву, учитывая величину x. При этом создается новый узел дерева. Обход дерева Функция, выполняющая обход дерева, позволяет перебрать все элементы, содержащиеся в дереве. В приведенной ниже реализации функция обхода дерева будет просто выводить на экран значение поля value каждого узла дерева (включая его корень):

template<class T> void walkTree(TNode<T>* p) { if(p) { walkTree(p->pleft); cout << p->value << ' '; walkTree(p->pright); } }

При работе с деревьями обычно используются рекурсивные алгоритмы. Использование рекурсивных функций менее эффективно, поскольку многократный вызов функции расходует системные ресурсы. Тем не менее, в данном случае использование рекурсивных функций является оправданным, поскольку нерекурсивные функции для работы с деревьями гораздо сложнее и для написания, и для восприятия кода программы. Например, нерекурсивная функция для обхода дерева может выглядеть так:

template<class T> void walkNotRec(TNode<T>* tree) { if (tree) { TNode<T> temp; TNode<T>* ptemp = &temp; TNode<T>* p = ptemp, *c = tree, *w; while (c != ptemp) { cout << c->value; w = c->pleft; c->pleft = c->pright; if(c == p) c->pright = 0; else c->pright = p; p = c; if (w) c = w; } } }

Применение Организация данных с помощью бинарных деревьев часто позволяет значительно сократить время поиска нужного элемента. Поиск элемента в линейных структурах данных обычно осуществляется путем последовательного перебора всех элементов, присутствующих в данной структуре. Поиск по дереву не требует перебора всех элементов, поэтому занимает значительно меньше времени. Максимальное число шагов при поиске по дереву равно высоте данного дерева, т.е. количеству уровней в иерархической структуре дерева.

17. Сбалансированные бинарные деревья. Вставка и удаление вершин.

Удаление узла из дерева – существенно более сложный процесс, чем поиск, так как удаляемый узел может быть корневым, левым или правым. Узел может давать начало ветвям (в двоичном дереве их может быть от 0 до двух).

Наиболее простым случаем является удаление терминального узла или узла, из которого выходит только одна ветвь.

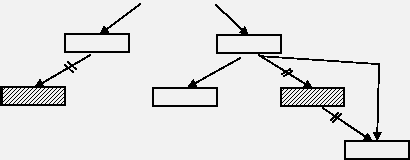Рисунок 4.10 – Удаление узла из дерева

Для этого достаточно скорректировать соответствующий указатель у предшествующего узла.

Наиболее трудный случай – удаление корневого узла поддерева (или всего дерева) с двумя ветвями, поскольку приходится корректировать несколько указателей. Нужно найти подходящий узел, который можно было бы вставить на место удаляемого, причем этот подходящий узел должен просто перемещаться. Такой узел всегда существует. Это либо самый левый узел правой ветви, либо самый правый узел левой ветви.

Если это самый правый узел левой ветви, то для достижения этого узла нужно перейти в следующий от удаляемого узел по левой ветви, а затем переходить в очередные узлы только по правой ветви до тех пор, пока очередной правый указатель не будет равен nil.

Такой узел может иметь не более одной ветви.

Пример удаления из дерева узла с ключом 50.

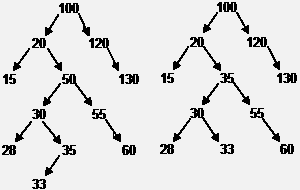Рисунок 4.11 – Пример удаления узла из дерева

Процедура удаления узла должна различать три случая:

- узла с данным ключом в дереве нет;

- узел с заданным ключом имеет не более одной ветви;

- узел с заданным ключом имеет две ветви.

Процедура удаления узла (автор - Никлаус Вирт)

Процедура удаления узла двоичного дерева на языке "Паскаль" procedure delnode(var d: ptr; key: integer); var q: ptr; procedure del1(var r:ptr); begin if r^.right = nil then begin q^.key := r^.key; q^.data := r^.data; q := r; r := r^.left end else del1(r^.right) end; begin if d = nil then exit     (* Первый случай *) else if key < d^.key then delnode(d^.left,key) else if key > d^.key then delnode(d^.right,key) else begin q := d;     (* Второй случай *) if q^.right = nil then d := q^.left else if q^.left = nil then d := q^.right else     (* Третий случай *) del1(q^.left); dispose(q)  (* Собственно удаление *) end end;

Вспомогательная рекурсивная процедура del1 вызывается только в третьем случае. Она проходит дерево до самого правого узла левого поддерева, начиная с удаляемого узла q^, и заменяет значения полей key и data в q^ соответствующими записями полей узла r^. После этого узел, на который указывает r можно исключить (r := r^.left).

Аналогичные функции на языке Си++: void del1(node*& r, node*& q) {     if (r->right == NULL)     {        q->key = r->key; // Перенос данных        q->data = r->data;        q = r;        r = r->left;     }     else        del1(r->right, q); } void del_node(node*& d, int key) {     node* q;     if (d == NULL)        return;     else        if (key < d->key)           del_node(d->left, key);        else           if (key > d->key)              del_node(d->right, key);           else           {              q = d;              if (q->right == NULL)                 d = q->left;              else                 if (q->left == NULL)                    d = q->right;                 else                    del1(q->left, q);              delete q;    // Удаление           } }