МАТЕМАТИКА ZIP File / Математика 2 сем Сам раб 140400 140100
.pdf1
Министерство образования и науки Российской федерации
Государственное бюджетное образовательное учреждение высшего профессионального образования
«Кузбасский государственный технический университет им. Т.Ф. Горбачева»
Г.А. Казунина, Г.А. Липина
Математика. 2 семестр: учебное пособие для самостоятельной работы студентов направлений подготовки 140400.62, 140100
« Электроэнергетика и электротехника»
«Промышленная теплоэнергетика»
Рекомендовано в качестве учебного пособия учебно-методической комиссией направления 140400.62 «Электроэнергетика и электротехника» 140100 « Промышленная теплоэнергетика»
Кемерово 2012
2
Рецензенты:
Жирнова Т.С. – доцент кафедры математики
Завьялов В.М. – председатель УМК направления подготовки 140400.62 «Электроэнергетика и электротехника»
Казунина Галина Алексеевна, Липина Галина Александровна. Математика. 2 семестр:
учебное пособие для самостоятельной студентов направлений подготовки 140400.62 «Электроэнергетика и электротехника» и 140100 «Промышленная теплоэнергетика» [Электронный ресурс] / Г.А. Казунина, Г.А. Липина - Электрон.дан.- Кемерово: КузГТУ, 2012.- 1электрон.опт.диск(CD-ROM); 12 см.- Систем. требования: любой компьютер, поддерживающий Microsoft Windows –97 и выше, мышь.- Загл. с экрана.
Приводятся элементы теории, примеры решения задач и содержание самостоятельной работы студентов по темам курса математики, которые согласно рабочей программе изучаются в 2 семестре. Для лучшего усвоения материала изложение сопровождается контрольными и тестовыми вопросами. Пособие предназначено для организации самостоятельной работы студентов
КузГТУ
Казунина Г.А. Липина Г.А.
3
Самостоятельная работа
РГР № 11 (0,278 ЗЕ) Срок выполнения 1- 4 недели
Кратные, криволинейные и поверхностные интегралы
Содержание работы
1.Вычисление кратных интегралов. Применение двойных и тройных интегралов к решению задач геометрии и физики (вычисление объема, момента инерции, координат центра масс)
2.Применение поверхностных и криволинейных интегралов 1 рода к решению задач геометрии и физики.
Литература [1, 2, 10, 16]
Двойные интегралы
Двойным интегралом от непрерывной функции f (x, y) по ограниченной замкнутой области D на плоскости 0XY называют предел последовательности интегральных сумм
|
n |
|
lim |
f (xk , yk ) sk |
f (x, y) ds . |
n k 1 |
D |
|
Вычисление двойного интеграла в декартовой системе координат сводится к последовательному вычислению однократных интегралов. Если область интегрирования ограничена сверху и снизу непрерывными кривыми y1 (x) и y2 (x) , а
слева и справа вертикальными прямыми x a, |
x b , то вычисление проводят |
по следующей формуле: |
|
b
f (x, y) ds dx
D |
a |
y
a
y2 ( x )
f (x, y) dy.
y1( x )
2 ( )
1( ) x
b
4
Если область интегрирования ограничена слева и справа непрерывными кривыми
x1 ( y), x2 ( y) , а снизу и сверху горизонтальными кривыми y c, |
y d , то |
||
вычисление проводят по формуле: |
|
|
|
|
d |
x2 ( y ) |
|
f (x, y) ds dy |
f (x, y) dx. |
|
|
D |
c |
x1( y ) |
|
y
d
2( )
1( )
c
x
В полярной системе координат интеграл вычисляют, выполнив замену переменной
:
|
|
r2 |
( ) |
|
f (x, y) ds d |
|
f (r cos , r sin ) rdr. |
D |
|
r ( ) |
|
|
|
1 |
|
Тройные интегралы
Тройным интегралом от непрерывной функции f (x, y, z) по ограниченной замкнутой пространственной области V называют предел последовательности интегральных сумм
|
n |
|
lim |
f (xk , yk , zk ) Vk |
f (x, y, z) dV . |
n k 1 |
V |
|
Вычисление тройного интеграла в декартовой системе координат сводится к последовательному вычислению однократного интеграла по одной из координат и двойного интеграла по проекции объема V на одну из координатных
плоскостей. Если область интегрирования ограничена сверху и снизу гладкими поверхностями z1 (x, y), z2 (x, y) , и однозначно проектируется на плоскость 0XY в область D , то интеграл вычисляют по формуле:
5
|
|
z2 |
( x, y ) |
|
f (x, y, z) dx dy dz dx dy |
|
f (x, y, z) dz . |
V |
D |
z1( x, y ) |
|
В тех случаях, когда объем проектируется на координатную плоскость в круг или часть круга, используют криволинейные системы координат. Так в цилиндрической системе координат интеграл вычисляют согласно соотношению:
|
|
|
|
|
|
z2( ,r) |
|
|
|
|
|
|
|
f (x, y, z) dx dy dz d rdr |
f (r cos , r sin , z) dz . |
||||||||
|
V |
|
|
D |
z1( ,r) |
|
|
|
|
||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
|||
1( ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
φ |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
+ 2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В тех случаях, когда пространственное тело ограничено сферическими поверхностями, удобно использовать сферическую систему координат, которая каждой точке пространства приписывает три координаты: полярный угол , азимутальный угол и расстояние от начала координат до точки на сфере r . Тройной интеграл при этом представляется в виде:
|
|
|
|
|
2 |
2 |
r2 |
( , ) |
|
|
|
|||
|
f (x, y, z)dx dy dz d cos d |
|
f (r cos cos , r cos sin , r sin ) r2dr |
|||||||||||
V |
|
|
|
|
|
|
|
r ( , ) |
|
|
|
|||
|
1 |
1 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϴcos |
|
|
|
|
|
M (φ, ϴ, r) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
sin |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
r sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ϴ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
Криволинейные и поверхностные интегралы 1 рода
Вычисление криволинейного интеграла 1-го рода (по длине дуги) сводится к вычислению определенного интеграла с учетом способа задания кривой и выражения для дифференциала длины дуги:
Кривая задана явно в декартовой системе координат
|
|
|
x a,b , |
b |
y y(x), dl |
2 |
dx , |
f (x, y(x)) dl ; |
|
1 ( y ) |
a
Кривая задана в полярной системе координат
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
r r( ), |
dl |
r |
2 |
|
|
2 |
d , f ( , r( ))dl ; |
|
|
||||
|
( ) (r ( )) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Кривая задана параметрически как векторная функция |
|
||||||||||||
|
|
|
|
z(t) , |
|
|
|
|
|
|
|
|
|
|
|
|
dl |
2 |
2 |
2 |
dt |
, |
|||||
r (t) x(t), y(t), |
(x ) |
( y ) |
(z ) |
||||||||||
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x(t), y(t), z(t))dl . |
|
|
||||||
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
Вычисление поверхностного интеграла 1-го рода (по площади поверхности)
сводится к вычислению двойного интеграла по проекции поверхности на какую-либо координатную плоскость. При проектировании поверхности
z z(x, y)на плоскость 0XY в область D дифференциал площади поверхности
d |
|
z 2 |
|
z 2 |
1 |
|
|
ds , а интеграл вычисляется по формуле |
|
|
|
x |
|
y |
f (x, y, z(x, y)) d f (x, y, z(x, y)) |
|
z 2 |
|
z 2 |
||
1 |
|
|
|
ds , |
||
|
||||||
|
D |
|
x |
|
y |
|
где дифференциал площади ds |
зависит от выбранной системы координат. |
|||||
ЗАДАЧИ
1.Запишите уравнения границ области интегрирования. Постройте область интегрирования. Измените порядок интегрирования в повторном интеграле.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
У |
|
|
2 |
|
|
2У У 2 |
|
||||||
|
а) dy |
|
|
|
|
|
f ( X ,У )dx dy |
|
|
f ( X ,У )dx ; |
|||||||||
|
0 |
|
|
|
|
2У У |
2 |
1 |
|
|
2У У |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Х 2 |
|
|
|
|
Х 2 |
|
|
|
||||||
|
3 |
|
|
|
2 |
|
|
|
|
||||||||||
|
б) dх |
f ( X ,У )dу dх |
|
f ( X ,У )dу ; |
|||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
3 |
Х |
2 |
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Вычислить интегралы: |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
1 x2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 y 2 2 |
|
|
|
|
|
|
|
|||||
|
а) |
dx |
|
|
dy (измените порядок интегрирования) |
|
||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X У 2dXdУ, |
D : X 2 У 2 а2 ; Х 0; |
|
|
|
||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
в) |
е X У dXdУ , |
D : У е Х ; Х 0; У 2 ; |
|
|
|
||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
ж) У 2 |
/( X 2 У 2 )dXdУ , D : X 2 У 2 |
4Х ; |
|
|
|
||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить площадь, ограниченную линиями: |
|
|
|||||||||||
3. |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||
|
x2 y2 4 y, |
x2 y2 6 y, |
y |
3 |
x, |
x 0 |
|
|
||||||
4. |
Вычислить тройной интеграл (выбрать подходящий порядок |
|||||||||||||
|
интегрирования): 8у 2 ze2xyz dxdydz;V : z [0;1] |
x [ 1;0] |
y [0;2] |
|||||||||||
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
5.Вычислить объем тела, ограниченного поверхностями, используя наиболее удобную систему координат:
x2 y 2 9x
а) x |
2 |
y |
2 |
12x |
б) x |
2 |
y |
2 |
z |
2 |
16 |
z 6 x |
2 |
y |
2 |
||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
в) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z |
|
x2 |
y 2 |
x2 |
y2 |
8(2 z) |
z |
x2 y2 |
|
||||||||||
z 0, |
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. Найти координаты центра масс:
а) тела с плотностью (X;У;Z)=X2+У2+Z2, заданного неравенствами а2 х2+ у2+z2 4a2; у 0;
7. Найти моменты инерции:
а) шара Х2 + У2 + Z2 а2 |
массой М и плотностью |
|||||
(X;У;Z) = |
|
С |
|
|
относительно центра; |
|
|
|
|
|
|||
|
|
|
|
|||
|
|
|||||
|
|
Х 2 У 2 |
Z 2 |
|
||
б) однородного тела: 0 Rz Н (R– 
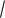Х 2 У 2 ) относительно OZ.
8
8. Найти массу, распределённую вдоль криволинейного отрезка У=Х2/2 с плотностью γ(X;У)=У/Х; Х [1;2];
9. Определить координаты центра масс однородной линии: x=е-tcost; y=e-tsint; z=e-t; t [0; );
10. |
Вычислить интеграл по части поверхности конуса |
|
|
|
, вырезанной цилиндром Х2+У2=2Х: |
Z |
X 2 У 2 |
|
|
|
( ХУ УZ XZ )d ; |
|
|
|
|
|
|
11. Определите координаты центра масс полусферы радиуса R с центром в начале координат с поверхностной плотностью =а
Х 2 У 2 ; а=const;
Контрольные вопросы
1.Какое множество является областью интегрирования для двойного, тройного, криволинейного, поверхностного интегралов?
2.Сформулируйте правило расстановки пределов по простейшей стандартной области для двойного интеграла в декартовой и полярной системах координат
3.Сформулируйте правило расстановки пределов для тройного интеграла в декартовой, цилиндрической системах координат
4.Тройной интеграл в сферической системе координат
5.Применение кратных интегралов к вычислению моментов инерции
6.Применение кратных интегралов к вычислению координат центра масс
7.Определение, вычисление и свойства интеграла от скалярной функции вдоль кривой
8.Определение, вычисление и свойства интеграла от скалярной функции по поверхности
Самостоятельная работа РГР № 12 (0,278 ЗЕ)
Элементы теории поля
Срок выполнения 1-4 недели
9
Содержание работы
1.Интеграл от векторной функции по кривой. Вычисление работы. 2. Потенциальное поле и его свойства.
3.Поток векторного поля. Дивергенция. Теорема Остроградского-Гаусса.
Литература [1, 2, 10, 16] |
|
|
|
Для векторного поля |
|
|
|
|
|||
A(x, y, z) Ax |
(x, y, z) i |
Ay (x, y, z) j |
Az (x, y, z) k |
Определены следующие дифференциальные операции первого порядка:
|
Дивергенция векторного поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A (M ) |
|
Ay (M ) |
|
|
A (M ) |
|
|
|
|||||
|
div A(M ) |
x |
|
|
|
|
|
|
|
z |
|
; |
|
|
|
|
x |
|
y |
|
|
z |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i |
|
|
|
j |
|
k |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ротор векторного поля rot A(M ) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
x |
|
|
y |
|
z |
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Ax (M ) |
Ay (M ) |
Az (M ) |
|
|||||||||
Интеграл от векторной функции вдоль кривой вводится согласно соотношению:
( A(M ), dr ) Ax (x, y, z)dx Ay (x, y, z)dy Az (x, y, z)dz ,
L L
а способ вычисления зависит от способа задания кривой, по которой ведется интегрирование:
Кривая задана уравнением |
y y(x), |
|
|||
dy y (x)dx , а интеграл |
|||||
|
|
|
b |
|
|
( A(M ), dr ) |
Ax (x, y(x)) dx Ay (x, y(x)) y (x) dx ; |
||||
L |
|
|
a |
|
|
Кривая задана параметрически как векторная функция |
|||||
|
y(t), z(t) . Тогда интеграл находят по формуле |
||||
r (t) x(t), |
|||||
10
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( A, dr ) |
Ax ( x(t), y(t), z(t))x (t) |
Ay ( x(t), y(t), z(t)) y (t) |
Az ( x(t), y(t), z(t))z (t) dt |
|||||
L |
|
t1 |
|
|
|
|
|
|
|
Условием |
потенциальности |
векторного поля |
дважды |
непрерывно |
|||
|
|
|
|
|
|
|
|
|
дифференцируемого в односвязной области является условие: |
rot A(M ) 0 . |
|||||||
Для такого поля определен потенциал U (x, y, z) - скалярная функция такая,
|
|
что |
A grad U (x, y, z) . В силу того, что интеграл от потенциального |
векторного поля вдоль кривой не зависит от контура интегрирования, одним из способов нахождения потенциала является интегрирование векторного поля по простейшему контуру, соединяющему две точки непрерывности поля линией, звенья которой параллельны координатным осям:
|
|
|
x |
y |
z |
|
|
(x, y0 , z0 ) dx Ay (x, y, z0 ) dy Az (x, y, z) dz C . |
|||
( A, dr ) Ax |
|||||
L |
|
|
x0 |
y0 |
z0 |
Потоком векторного поля называют интеграл от векторной функции по поверхности z z(x, y) , ориентация которой определяется выбором
направления нормали |
|
|
z |
, |
|
z |
|
: |
N |
x |
y |
1 |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
( A, d ) ( A, N ) ds . |
|||
|
|
D |
|
Поток векторного поля через замкнутую ориентированную поверхность находят с помощью теоремы Остроградского-Гаусса:
|
|
|
( A, n) d div AdV . |
||
|
|
V |
Циркуляцию дифференцируемого векторного поля (интеграл по замкнутому контуру) находим по теореме Стокса:
( A, dr )
C
ЗАДАЧИ
(rot A,
n) d (rot A, N ) ds .
D
1.Найти производные первого порядка векторных полей. Определить, какие из полей являются потенциальными. Для потенциальных полей найти потенциал.
а) А (3x2 y y3 )i (x3 3xy 2 ) j ;