Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТЕМАТИКА ZIP File / Математика 2 сем Сам раб 140400 140100

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

2.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

	2 i	2 i 1 2i	5i
				i .
1 2i		1 2i 1 2i	5

Итак, f 1 2i 7 24i i 3 2i 4 23i .

Пример 2. Решить уравнение 2 i z2 5 i z 2 2i 0 .

По формуле для корней квадратного уравнения имеем:


	5 i	5 i 2 4 2 i 2 2i
z				5 i 2i	.
		2 2	i
1,2				4 2i

Извлекая корень квадратный из числа 2i , получим:

2i 1 2i 1 1 i 2 1 i .

Следовательно,

5 i

. Отсюда

1,2

4 2i

5 i 1 i

6 2i

3 i

3 i 2 i

5 5i

1 i

4 2i

2 i

2 i 2 i

5 i 1 i

2 2 i

i .

4 2i

2 i

2 i 2 i

Тригонометрическая и показательная формы комплексного числа

Рассмотрим полярную систему координат на плоскости, совместив

полюс с началом координат, а полярную ось направив по оси	OX. Тогда
комплексному числу z x iy 0 будут соответствовать	полярные

координаты r и . Число r называют модулем комплексного числа:

r z x2 y2 .

Геометрический смысл модуля комплексного числа – длина вектора,

изображающего комплексное число (рис. 1). Полярную координату называют аргументом комплексного числа:

Argz

При этом угол – это угол между вектором, изображающим комплексное число и положительным направлением оси OX (рис. 1). Аргумент

комплексного числа Argz многозначен и определяется с точностью до

значения, кратного числу 2 . Главным значением аргумента аrgz называют

угол, удовлетворяющий условиям arg z .

Тогда Argz arg z 2 n 2 n.

Для определения главного значения аргумента комплексного числа следует учитывать, какой четверти комплексной плоскости соответствует комплексное число:

φ=

					φ=0





	+

Приведем примеры определения модуля и аргумента комплексного числа. Пример 3. z 2.

Число z 2 является действительным. Поэтому x 2 ; y 0

z 2 ; arctg xy arctg0 0.

Пример 4. z 2.

Число z 2 является действительным.

Поэтому x 2 ; y 0

z 2 ; .

Такое значение аргумента соответствует любому действительному отрицательному числу.

Пример 5. z i .				x 0 , а y 1.
Число z i чисто мнимое				x 0 , а y 1.
	z	1;	.
	z	1;	.
			2
			2

Такой аргумент соответствует всем чисто мнимым числам iу при условии у 0 .

Пример 6. z i .

Это также чисто мнимое число. z 1, но 2 , так как вектор

соответствующий комплексному числу направлен вдоль оси OY в отрицательную сторону.

Пример 7.

z 1 i .

Здесь x Re z 1; y Im z 1

arctg

arctg1 .

1 1

2 ;

z 1 i .

Пример 8.

Здесь x 1;

y 1. Вектор, изображающий число, лежит во второй

четверти. Поэтому arctg

arctg1

x2 y2

Пример 9.

z 1

3i .

Здесь x 1;

1 3

arctg

Понятие модуля и аргумента комплексного числа позволяют представить комплексное число в тригонометрической форме:

x rcos ; y rsin ;

z x iy rcos irsin r cos isin .

Пример 10. Согласно примерам 9,5, 7 получаем:

						2		2
						2		2
z 1	3i		2 cos				i sin		;
z 1	3i		2 cos				i sin		;
						3		3
z i cos		i sin			;
	2			2
z 1 i					i sin

		2 cos					.
				4			4

Разложение стандартной экспоненты в ряд Маклорена позволяет определить показательную функцию с мнимым показателем:

exp i 1 i					1	i 2		1		i 3			1	i 4			1	i 5	...
exp i 1 i						i 2				i 3				i 4				i 5	...
					2!			3!					4!				5!
	1	2	1	4					1		3		1		5
1					...		i x									...
1					...		i x									...
	2!		4!						3!			5!
С учетом разложения в ряд функций sin ,															cos :

sin 31! 3 51! 5 71! 7 ...; cos 1 21! 2 61! 6 81! 8 ...;

получаем формулу Эйлера

ei cos isin .

Формула Эйлера позволяет записать комплексное число в показательной форме

z x iy r cos isin re i .

Пример 11. Продолжая примеры 9 ,5,7 можно записать числа в показательной форме

		2		2		2	i
		2		2			i
z 1	3i 2 cos		i sin		2e	3 ;
z 1	3i 2 cos		i sin		2e	3 ;
		3		3

z i cos 2 i sin 2 ei 2 ;

z 1 i			i sin

	2 cos
		4		4

2ei 4 .

Запись комплексного числа в показательной и тригонометрической формах очень удобна для выполнения операций умножения, деления, возведения в степень и извлечения корня.

Пусть заданы комплексные числа:

																			z r ei 1								и z				2		r ei 2 .
																				1	1										2				2
				Тогда справедливо:
	z z				2		r r ei 1 ei 2										r r ei 1 i 2											rei
1)	1				2			1		2								1		2
1)	r cos i sin ,
где r r1								r2 ;			1 2 .
2)		z1					r1ei 1				rei 1 2							rei			r cos i sin ,
2)		z	2				r ei 2				rei 1 2							rei			r cos i sin ,
		z					r ei 2
						2
где r						r1		;								.
где r						r2		;					1		2	.
													1		2

3)		zn		rei n r n ei n														r n cos n i sin n .
												2 k										2 k
4)	n z n											2 k							i sin			2 k
4)	n z n								r cos										i sin											. k 0,1, 2, 3,...,n 1.
														n											n
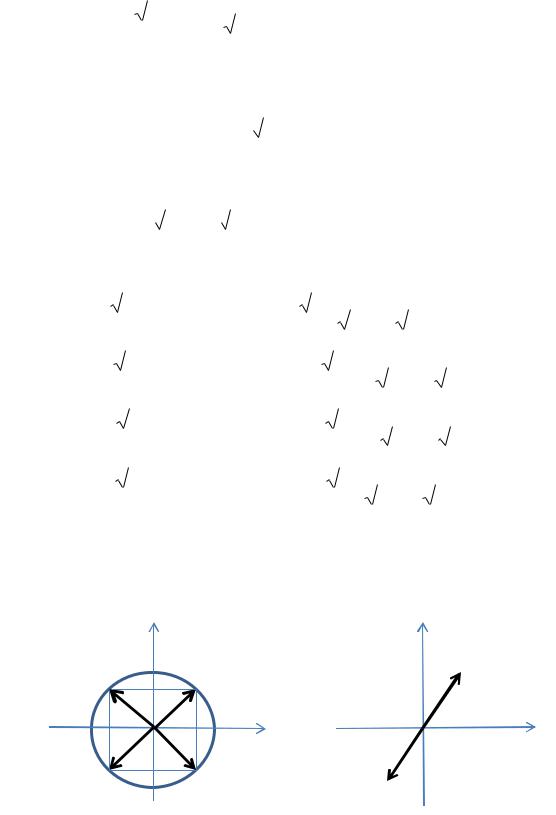
				Заметим, что корни из комплексного числа лежат в вершинах

правильного n -угольника, вписанного в круг радиуса n r .
																							1										24
																																	24
Пример 12. Выполним действия																														3i
Пример 12. Выполним действия																							1				i						.
																							1				i
																																2		i
							С учетом того, что 1																	3		i 2e							3	i	, 1 i					2	e 4 i , получаем
																	2		i
							1 3i 2e																2															5
																	3						2															5

																						2	e 3					4								2	e 12 .
																													i										i

1 i		i

	2e 4

	1							i 24								5				24
							3									5			i						212 e10 i
							3												i
												2e 12
		1	i
		1	i
	212 cos10 i sin 10 212

Пример 13. Найдем все корни 4																	4						.
	Число z 4 имеет r																				z			4 и аргумент .
	Число z 4 имеет r																				z			4 и аргумент .
	С учетом этого, все корни можно найти по формуле
																						2 k															2 k
										4 4												2 k							i sin								2 k
			4							4 4				4 cos															i sin														;
																									4														4
																		k 0,1, 2, 3.
k 0 ,												i sin															1				i				1				1 i ;
																											1								1
	z1			2 cos					4						4											2

																											2									2
																											2									2
k 1,									3				i sin				3																1			i			1				1 i ;
									3								3																1						1
	z2				2 cos																						2
										4
																																	2							2
																		4															2							2
k 2,										5			i sin					5															1				i		1				1 i ;
										5								5															1						1
	z3					2 cos																						2
											4
																																	2
																			4														2								2
k 3,										7			i sin					7												1				i				1				1 i .
										7								7												1								1
	z4					2 cos																						2
											4
																																2							2
																			4													2							2

Расположение корней на комплексной плоскости показано на рис. 4.



		1
	1

2

		x
	4	2

Рис.4

									1
Пример 14. Найдем									1						3i .
																			1								2, а аргумент							2
		С учетом того, что												z									3			i								2	, получаем
		С учетом того, что												z									3			i								3	, получаем
		(рис. 5)																																3
		(рис. 5)
										2												2
													2 k														2 k
											3		2 k								3						2 k
	1			i				cos										i sin													,
			3				2
			3				2
												2																2


k 0,1.

																									1					3


k 0 ,		z1				2 cos					i sin																	i				;
k 0 ,		z1				2 cos					i sin									2								i				;
									3							3								2						2
									4								4
																													1			3

k 1,												i sin																		i
		z2			2 cos																			2									.
		z2			2 cos																			2									.
									3								3												2			2

ЗАДАЧИ

1. Провести вычисления в алгебраической форме:

2 i		i5	2	2
	(i 1)(2 3i);
5 i	(i 1)(2 3i);	19	1
5 i		i	1

2.Для указанных комплексных чисел определите реальную часть , мнимую часть, модуль и аргумент . Построить вектор комплексного числа на плоскости. Записать число в тригонометрической и показательной формах:

z 4	z 4	z 2i	z 3i

z 1 i		z 2 2i	z 4 4i
	z 1 3i

3.Проведите вычисления, используя показательную и тригонометрическую форму записи комплексного числа. Дайте геометрическую интерпретацию операции извлечения корня:

1		24

	3i
	3i
			;	4	4 ;	3	8	;	6	1 ;	4	1	i
1 i			;		4 ;		8	;		1 ;		1	i
1 i

			38

4. Найдите корни уравнений:

	z2 6z 13 0 ;	z2 8z 20 0 ;	z3 27 0;

2.Функции комплексной переменной

Понятие функции комплексной переменной. Если каждому комплексному числу z , принадлежащему области D (связное открытое множество), поставлено в соответствие некоторое комплексное число w , то говорят, что в области D определена функция комплексной переменной w f (z) , которая может быть представлена с помощью двух действительных функций U (x, y) и V (x, y) действительных аргументов:

	w U(x, y) iV (x, y) ,
где U(x, y) Re f (z),	V (x, y) Im f (z) .

К основным элементарным функциям относят:

Степенную функцию zn ;

Показательную функцию ez ex (cos y i sin y) ;

Тригонометрические функции

sin z

ei z e i z

cos z

ei z e i z

, tgz

sin z

, ctgz

cos z

;

cos z

sin z

Гиперболические функции

shz

e z e z

ez e z

thz

sh z

, ctgz

ch z

;

, ch

ch z

sh z

Логарифмическая

функция

Ln z ln

i (arg z 2k )

является

многозначной. В каждой точке z 0,

она принимает бесконечно

много

значений.

Выражение

ln z ln

i arg z

называют

главным

значением логарифмической функции;

Общая степенная функция za ea Ln z является многозначной. В частном случае a n1 получаем многозначную функцию – корень n -й степени из

комплексного

числа:

(ln

i (argz 2k )

(cos

arg z 2k

i sin

arg z 2k

n z en

Общая показательная функция az ez Lna является многозначной;

Обратные тригонометрические и гиперболические функции выражаются

через логарифмическую функцию и являются многозначными

Arc cosz iLn(z z2 1) .

Интеграл от функции комплексной переменной вводится аналогично интегралу от векторной функции вдоль кусочно-гладкой кривой:

f (z) dz U (x, y)dx V (x, y)dy i V (x, y)dx U (x, y)dy .

L L

Функция f (z) , дифференцируемая в некоторой области, и имеющая в этой области непрерывную производную f (z) , называется аналитической в этой области. Необходимые и достаточные условия аналитичности в некоторой области выражаются следующими соотношениями:

Существование непрерывных частных производных функций U(x, y), V (x, y) , которые удовлетворяют условиям Коши-

Римана:	U		V	;	U		V	;
	x		y		y		x

Интеграл по кривой не зависит от контура интегрирования, и справедлива формула Ньютона-Лейбница:

z2 f (z) dz F (z2 ) F (z1 );

Интеграл от аналитической функции по замкнутому контуру, который ограничивает односвязную область, равен нулю

(теорема Коши для односвязной области):

f (z) dz 0 ;

Теорема Коши для многосвязной области:

f (z) dz f (z) dz ;

k Ck

Если функция f (z) аналитична в некоторой области D , а контур C принадлежит этой области и охватывает точку z0 , то

справедлива интегральная формула Коши, которая связывает значение функции в точке с интегралом по контуру:

f (z0 )	1		f (z)		dz.
	2 i		z z
		C		0

При этом функция f (z) имеет в области D производные, для которых справедливы формулы:

f (n) (z )	n!		f (z)	dz, n 1,2
f (n) (z )	2 i		(z z )n 1	dz, n 1,2
0	2 i		(z z )n 1
0
		C	0

В окрестности точки аналитичности z0 функция f (z) представляется рядом Тейлора


f (z) ck (z z0 )k ,
k 0
областью сходимости которого является круг z z0	R , радиус

которого равен расстоянию от точки аналитичности до ближайшей особой точки.

В окрестности особой точки z0 функция f (z) представляется

рядом Лорана:

	C k
	C k		k
f (z)			Ck (z z0 )	,
f (z)	(z z	)k	Ck (z z0 )	,
k 1	(z z	)k	k 0
	0

который состоит из главной (по отрицательным степеням) и правильной (по положительным степеням) частей. При этом областью сходимости является кольцо r z z0 R .

Точка z0 называется изолированной особой точкой функции f (z) ,

если однозначная функция аналитична в открытом круге 0 z z0 R .

Основой для классификации особых точек является вид разложения в ряд Лорана в окрестности точки:

Устранимая особая точка – ряд содержит только правильную часть (предел в точке существует и конечен)

f (z) ck (z z0 )k ;

k 0

Существенно особая точка – ряд содержит бесконечное число членов в главной части (предел в точке не существует)

	C k
	C k		k
f (z)			Ck (z z0 )	;
f (z)	(z z	)k	Ck (z z0 )	;
k 1	(z z	)k	k 0
	0

Полюс порядка m - ряд содержит конечное число членов в главной части, равное m , в главной части (в точке существует бесконечный предел).

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в папке МАТЕМАТИКА ZIP File

#
10.05.20152.69 Mб39Математика 2 сем Сам раб 140400 140100.pdf
#
10.05.20151.35 Mб54МУ к самост раб 1 сем 140400.doc
#
10.05.20151.13 Mб38МУ к самост раб 1 сем 140400.pdf
#
10.05.20151.49 Mб43Практические бак 1 семестр.doc