МАТЕМАТИКА ZIP File / Математика 2 сем Сам раб 140400 140100
.pdf
71
H ( p) :
p2Y( p) pY( p) x( p) 1,
H( p) |
Y( p) |
|
1 |
. |
|
|
|||
X ( p) |
p( p 1) |
Возвращаясь к оригиналам, получаем функцию Грина:
w(t) (1 e t ) (t).
Теперь, задавая любым образом правую часть x(t), можно найти решение дифференциального уравнения.
Пусть x(t) e2t (t). Тогда
t |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
y(t) x(t )w( )d e2(t ) (1 e )d |
|
||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
t |
|
|
|
|
|
|
1 |
|
t |
|
1 |
|
t |
|
|
e2t (e 2 e 3 )d e2t ( |
e 2 |
|
e 3 |
) |
|||||||||||
2 |
|
||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
3 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( |
1 |
|
1 |
e t |
1 |
e2t ) (t). |
|
|
|
|
|||||
2 |
|
6 |
|
|
|
|
|||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
Пример 9. Найти частное решение дифференциального уравнения
y y x(t) , y(0) 0. .
Правая часть уравнения задана функцией
x(t)
2
0 |
2 |
t |
72
0, t 0,
1
x(t) t 1, 0 t 2,
2
0, t 2.
Для применения формулы свертки следует записать x(t) , используя ступенчатые функции Хевисайда:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
t |
1 (t) |
|
|
|
|
|
|
(t 2) 2 (t 2). |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С |
|
учетом |
|
|
того, |
что |
|
функция |
|
Грина |
|
для |
этого |
уравнения |
имеет вид |
||||||||||||||||||||||||||||||||||
w(t) e t (t), получаем решение y(t) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
1 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y(t) |
|
( 2)e (t ) d |
( 2) ( 2)e (t ) (t )d |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
e t |
2 e d (t) |
|
e t ( 2)e d (t 2) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
e |
t |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
e |
|
2 e |
|
e |
|
|
0 (t) |
|
|
|
|
( |
2)e |
e |
|
|
|
(t 2) |
|
||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
e t tet |
2et et 1 (t) |
e t |
|
(tet 2et et 4e2 e2 ) (t 2) |
||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
e t |
(t) |
|
|
|
|
|
|
|
|
t |
|
|
|
|
e (t 2) (t |
2) |
|
|
||||||||||||||||
|
|
|
|
|
|
2 |
|
2 |
2 |
|
2 |
2 |
|
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
73
21 (t e t 1) (t) 21 ( t 1 3e (t 2) ) (t 2).
Другой способ записи решений дифференциальных линейных уравнений с использованием свертки основан на формуле Дюамеля. Характеристикой
системы в этом случае служит переходная функция h(t) , которая определяется как реакция (отклик) системы на постоянное воздействие
x(t) (t) 1p :
Y ( p) H( p) X ( p) |
H( p) |
; |
h(t) Y ( p). |
|
|||
1 |
p |
|
1 |
|
|
|
Из последнего выражения и свойства интегрирования оригинала
следует, что функция w(t) и h(t) связаны соотношениями:
t
h(t) w( )d , h (t) w(t).
0
С учетом того, что
H( p) pY1 ( p) ,
Y( p) H( p) X ( p) pY1 ( p) X ( p),
оригинал
y(t) можно записать по формуле Дюамеля следующим образом:
t |
t |
y(t) h(0)x(t) h ( )x(t )d h(0)x(t) h (t )x( )d
0 |
0 |
t |
t |
h(t)x(0) x ( )h(t )d h(t)x(0) |
x (t )h( )d . |
0 |
0 |
74
Заметим, что при условии h(0) 0 две первых формы записи решения совпадают с записью
t
y(t) w( )x(t )d .
0
Также напомним, что в силу условий вывода формулы Дюамеля приведенные формулы можно непосредственно использовать для непрерывных функций x(t)
. В том случае, если функция x(t) имеют точки разрыва первого рода, следует
точно записывать эту функцию, учитывая скачкообразное изменение функции в точках разрыва или другим способом учесть эти изменения. Например, если
правая часть x(t) имеет вид:
f (t), 0 t T;
x(t) 0, t T,
L x (t) pF( p) f (0) f (T)e pT ,
то и формула Дюамеля принимает вид:
Y( p) pY1 ( p) X ( p) pY1 ( p) X ( p) x(0)Y1 ( p) x(T)e pT Y1 ( p)
x(0)Y1 ( p) x(T)e pT Y1 ( p)
Y1 ( p) px( p) x(0) x(T)e pT x(0)Y1 ( p) x(T)e pT Y1 ( p).
Переходя к оригиналам, получаем
t
y(t) x(0)h(t) (t) x ( )h(t )d x(T )h(t T ) (t T ).
0
Применим формулу Дюамеля для решения примера 9.
75
Пример 9 (продолжение)
Производная функции, стоящей в правой части уравнения равна:
x (t) |
1 |
(t) (t 2) . |
x (t) |
|
2 |
||||
|
|
|
||
|
|
|
1/2 |
0 2 t
Переходная функция системы имеет вид:
h(t) 1 e t (t).
Тогда вычисляя по формуле
t
y(t) x(0)h(t) x (t)h(t )d x(T)h(t T) (t T)
0
с учетом того, что x(0) 1, |
|
x(2) 2 , получаем: |
|||||||||||
|
|
|
1 |
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
x(t) |
1 e t |
(t) |
|
|
|
1 e (t ) |
d (t) |
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
2 1 e (t 2) |
|
(t |
2) |
|
1 |
e t |
(t) |
|||||
|
e (t |
) |
|
|
|
|
|||
|
|
||||||||
1 |
d (t 2) |
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
t 1 |
e t |
(t) |
|
|
||
|
|
|
|
|
|
||||
21 t 3 e (t 2) (t 2) 2 1 e (t 2) (t 2)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
t e t (t), |
||||||||
1 |
|
t |
|
|
1 |
|
|
|
(t 2) |
|
|
|
2 |
||||||||||
1 t e |
(t) |
|
|
t 1 |
3e |
(t 2) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
3 |
(t 2) |
|
1 |
|
t |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
e |
|
2 |
e |
|
, |
|||
0 t 2, t 2.
76
ЗАДАЧИ
1. Решите линейные дифференциальные уравнения с использованием свертки (формула Грина, формулы Дюамеля)
а) Решите дифференциальное уравнение |
|
y y x(t) |
для правых частей |
||||
|
y(0) 0 |
||||||
|
|
|
|
|
|
||
различного вида |
|
|
|
|
|
|
|
1) x(t) t, |
2) x(t) exp(2t), |
3) x(t) sin(2t), |
|
|
|||
|
|
|
2 |
2 |
|
|
|
4) x(t) 2 (t) (t 2) (t |
3), 5) x(t) ( |
|
t 2) (t) |
|
(t 3) 4 (t |
3) |
|
|
|
||||||
|
|
|
3 |
3 |
|
|
|
Ответы:
1)y(t) t 1 e t , 2) y(t) 13 e 2t e t ,
3)y(t) 15 sin 2t 2 cos 2t 52 e t
4)y(t) 2(1 e t ) (t) (1 e (t 2) ) (t 2) (1 e (t 3) ) (t 3)
5)y(t) 23 t 2 2e t (t) 23 (t 3) 5(1 e (t 3) (t 3)
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
t |
|
b) y |
|
y |
|
10e |
|
|
|
y |
2 y |
2 y 2e |
tgt |
||||
|
|
|
|
|
f) |
|
|||||||||
|
|
|
|
|
y |
0 |
|
y(0) |
y |
|
0 |
|
|
||
y(0) y (0) |
(0) |
|
(0) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы:
1. Модуль и аргумент комплексного числа
2. Запись комплексного числа в показательной и тригонометрической формах
3. Степенная функция комплексного аргумента. Свойства
77
4.Показательная функция комплексного аргумента. Свойства
5.Логарифмическая функция комплексного аргумента. Свойства
6.Тригонометрические функции комплексного аргумента. Свойства.
7.Гиперболические функции комплексного аргумента. Свойства
8.Обратные тригонометрические функции комплексного аргумента. Свойства.
9.Обратные гиперболические функции комплексного аргумента. Свойства.
10.Понятие аналитической функции. Теорема Коши для односвязной и
многосвязной областей
11.Ряд Тейлора. Область сходимости. Ряд Лорана. Область сходимости
12.Классификация изолированных особых точек.
13.Вычет аналитической функции в изолированной конечной особой точке.
Вычет аналитической функции в бесконечно удаленной особой точке
14.Применение вычетов к вычислению контурных интегралов
15.Применение вычетов к вычислению несобственных интегралов
16.Определите характер особой точки z 0 для функций
a) f (z) |
sin z |
; b) |
f (z) sin(1/ z); |
c) f (z) |
1 |
|
z |
z sin z |
|||||
|
|
|
|
17.Вычислить |
|
|
|
|
|
|
dz |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
||||||||
|
z |
|
|
0,5 z3 1 |
|||||||
|
|
|
|||||||||
18.Вычислить |
|
|
|
|
|
|
|
dz |
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 z10 1 |
|||||||
|
z |
|
|
|
|
||||||
|
|
|
|
|
|||||||
19.Вычислить |
|
|
|
|
|
|
dz |
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 z21 |
||||||||
|
z |
|
|
||||||||
|
|
||||||||||
20.Особенности ряда Фурье для четной и нечетной функции
21.Преобразование Лапласа. Функция-оригинал.
22.Обратное преобразование Лапласа. Теоремы разложения.
23.Решение линейных дифференциальных уравнений операторным методом
24.Формулы Грина и Дюамеля. Применение к решению линейных дифференциальных уравнений
78
25.Установите соответствие между комплексным числом и его модулем
1. 
2. 
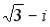
3. 
4. 
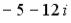
Варианты ответов:
5 , |
2 , |
3 , |
13 , |
, |
26.Установите соответствие между комплексным числом и его аргументом
1. 
2. 
3. 
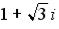
Варианты ответов:
, |
, |
, |
27.Установите соответствие между комплексным числом и его аргументом
1. 
2. 
3. 
Варианты ответов:
, |
, |
, |
28.Установите соответствие между комплексным числом и его аргументом
1. 
2. 
3. 
79
Варианты ответов:
, |
, |
, |
29.Установите соответствие между комплексными числами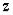 
и их аргументами
1. 
2. 
3.
Варианты ответов:
, |
, |
, |
, |
30.Произведение комплексного числа 
на сопряженное число 
равно…
31.Частное 
от деления двух комплексно сопряженных чисел, где 
, равно…
32.Дано: |
, тогда |
равно … |
|
33.Произведение комплексного числа |
и сопряженного числа |
равно |
|
… |
|
|
|
34.Произведение комплексного числа |
и сопряженного числа |
равно … |
|
35.Значение функции |
в точке |
равно… |
|
36.Значение функции |
в точке |
равно… |
|
37.Значение функции |
в точке |
равно… |
|
80
38.Значение функции |
|
в точке |
равно… |
39.Значение функции |
|
в точке |
равно… |
40.Дана функция |
, |
. Тогда коэффициент b4 разложения |
|
в ряд Фурье равен… |
|
|
|
41.Дана функция |
, |
. Тогда коэффициент b3 разложения |
|
в ряд Фурье равен… |
|
|
|
42.Дана функция |
, |
. Тогда коэффициент а2 разложения |
|
в ряд Фурье равен… |
|
|
|
43.Дана функция |
, |
|
. Тогда коэффициент b4 разложения |
в ряд Фурье равен… |
|
|
|
44. Комплексное число |
можно представить в виде … |
||
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
1) |
, 2) |
, 3) |
Самостоятельная работа
РГР № 15 (0,556 ЗЕ)
Теория вероятностей и математическая статистика
Содержание работы