1.5 Построение планов ускорений

Построение планов ускорений рассмотрим для второго положения механизма. Так как кривошип ОА вращается с постоянной угловой скоростью, то точка А будет иметь только нормальное ускорение, величина которого равна:

а направленно оно параллельно звену ОА от точки А к точке О.

Определяем масштабный коэффициент плана ускорений:

Последовательность построения плана ускорений рассмотрим для седьмого положения механизма.

Из произвольной точки π – полюса плана ускорений откладываем вектор параллельно звену ОА от точки А к точке О.

Для построения точки В и В' составим и решим графические уравнения:

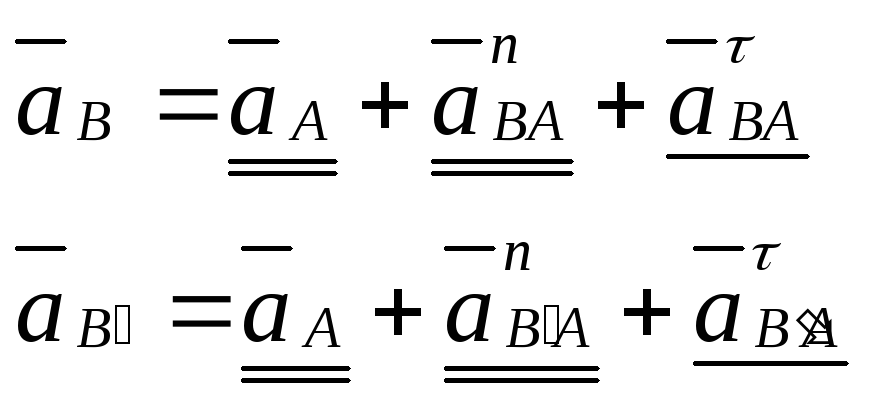
Ускорение направлено параллельно ОВ проведенное через полюс.

Ускорение направлено параллельно ОВ' проведенное через полюс.

Определим модули нормальных ускорений:

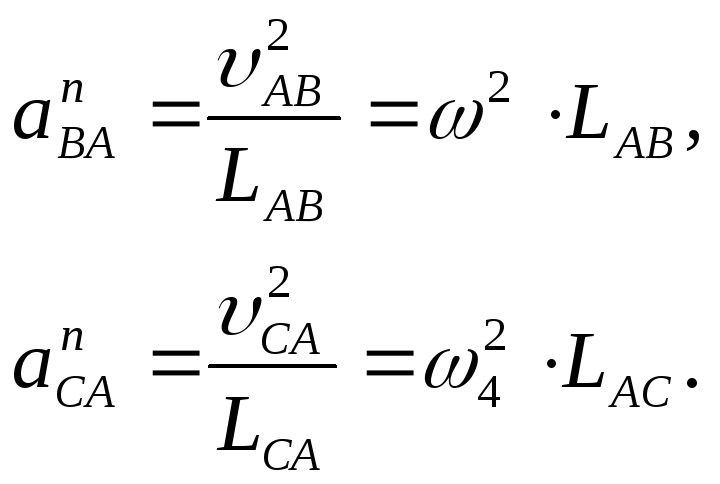
Нормальное ускорение направлено параллельно звену АВ от точки В к точке А (центру вращения).

Нормальное ускорение направлено параллельно звену АС от точки С к точке А.

Для 0 положения

Для 2 положения

Для 10 положения

Тангенциальные составляющие ускорений ипо абсолютной величине неизвестны, но известны по направлению. Они направлены перпендикулярно соответствующим звеньям механизма АВ и АС или перпендикулярно нормальным составляющим.

Согласно первому векторному уравнению через точку а плана ускорений проводим прямую, направленную вдоль звена АВ в направлении от точки В к точке А и на ней откладываем отрезок a =8 мм, величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения .

Через точку перпендикулярно звену АВ (или тоже самое, что перпендикулярно) проводим направление вектора тангенциального ускорения, до пересечения с линей действия вектора(параллельно к ОВ, проведенный через полюс ). Получим точку В.

Согласно второму векторному уравнению через точку а плана ускорений проводим прямую, направленную вдоль звена АC в направлении от точки C к точке А и на ней откладываем отрезок =3 мм. величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения.

Через точку перпендикулярно звену АC проводим направление вектора тангенциального ускорения , до пересечения с линей действия вектора(параллельно к ОC, проведенный через полюс ). Получим точку C.

Для определения ускорений точек S₂ и S₄ – центров тяжести звена 2 и звена 4 воспользуемся теоремой подобия.

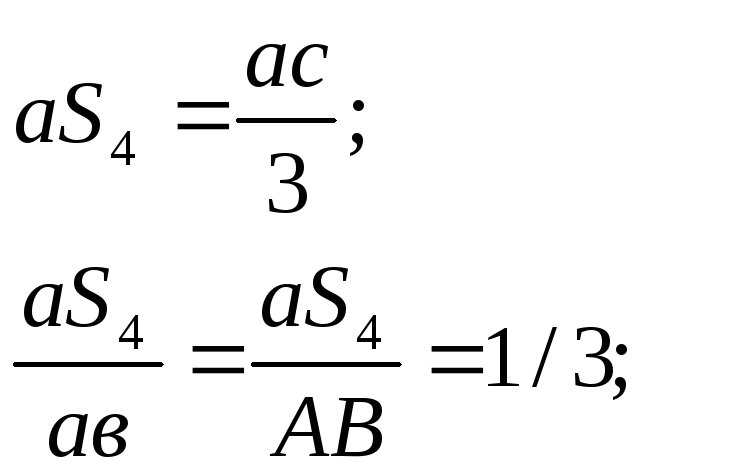
Определяем действительное значение ускорений:

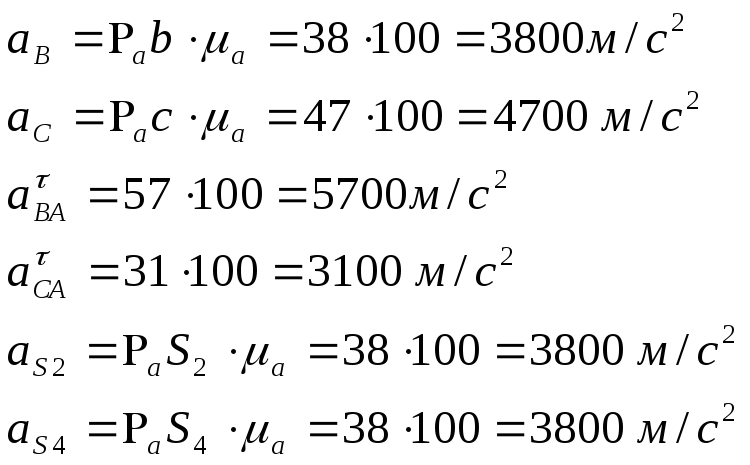
План ускорений для положений механизма 1 и 6 строим аналогично. Ускорение всех точек звеньев механизма и их отрезки сводим в таблицу 4.

Таблицу 4. Абсолютные и относительные ускорение точек

звеньев механизма и их отрезки в миллиметрах

Обозначение		Единица	Положение механизма
			0	2		10
		мм	65	65		65
аА		м/с2	6552	6552		6552
		мм	44	45		38
аB		м/с2	4400	4500		3800
	мм		16		65	47
АC	м/с2		1600		6500	4700
	мм		0		57	57
	м/с2		0		570	5700
	мм		67		31	31
	м/с2		6700		3100	3100

Угловые ускорения звеньев определяются на основе построенных планов ускорений.

Входное звено 1 вращается равномерно с постоянной угловой скоростью. Следовательно, его угловое ускорение равно нулю:

Модули угловых ускорений второго и четвертого звеньев для второго положения механизма можно найти по формулам:

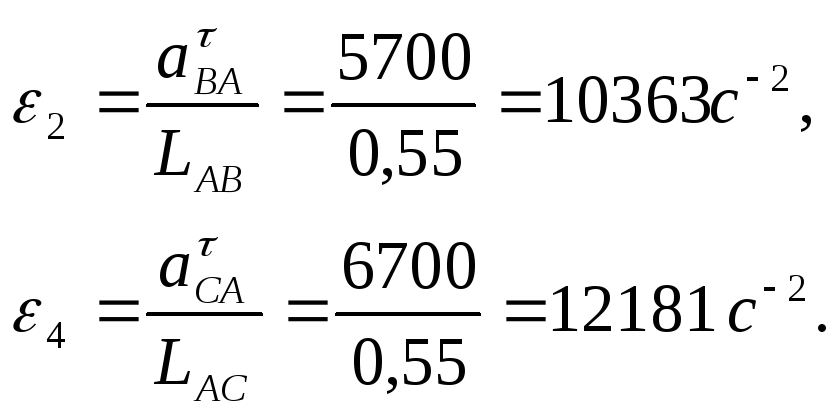
Таблица 5. Значение угловых ускорений шатуна АВ и АВ' в с^-2

Обозначение	Единица	Положение механизма
		0	2	10
ε2	с-2	0	10363	10363
ε4	с-2	12181	5656	5656

Определим направления угловых ускорений звеньев 2 и 4. Чтобы определить направление углового ускорения ε₂ необходимо вектор относительного тангенциального ускорения с плана ускорений перенести в точку В механизма, а точку А условно закрепить.