Пусть задана некоторая прямоугольная система координат и прямая. Пустьи две различные плоскости, пересекающиеся по прямой и задаваемые соответственно уравнениямии. Эти два уравнения совместно определяют прямуюв том и только в том случае, когда они не параллельны и не совпадают друг с другом, т. е. нормальные векторыиэтих плоскостей не коллинеарны.

Определение. Если коэффициенты уравнений

и (3.17)

не пропорциональны, то эти уравнения называются общими уравнениями прямой, определяемой как линия пересечения плоскостей.

Определение. Любой ненулевой вектор, параллельный прямой, называется направляющим вектором этой прямой.

Выведем уравнение прямой , проходящей через данную точкупространства и имеющей заданный направляющий вектор.

Пусть точка  произвольная точка прямой . Эта точка лежит на прямой тогда и только тогда, когда вектор, имеющий координаты, коллинеарен направляющему векторупрямой. Согласно (2.28) условие коллинеарности векторовиимеет вид

. (3.18)

Уравнения (3.18) называются каноническими уравнениями прямой, проходящей через точку и имеющей направляющий вектор.

Если прямая задана общими уравнениями (3.17), то направляющий векторэтой прямой ортогонален нормальным векторамиплоскостей, задаваемых уравнениямии. Векторпо свойству векторного произведения ортогонален каждому из векторови. Согласно определению в качестве направляющего векторапрямойможно взять вектор, т. е..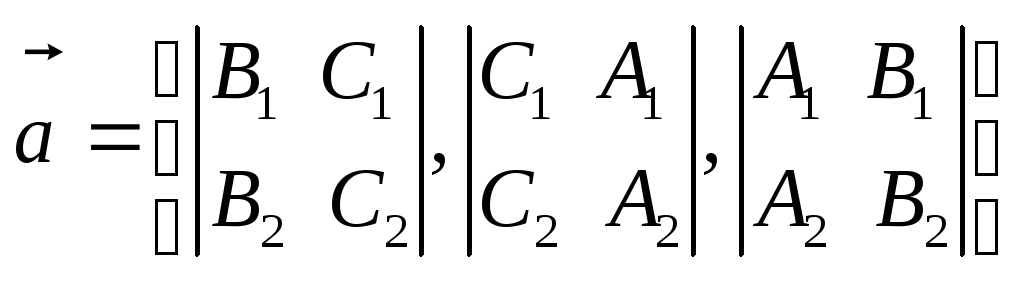

Для нахождения точки рассмотрим систему уравнений. Так как плоскости, определяемые уравнениямии, не параллельны и не совпадают, то не выполняется хотя бы одно из равенств. Это приводит к тому, что хотя бы один из определителей,,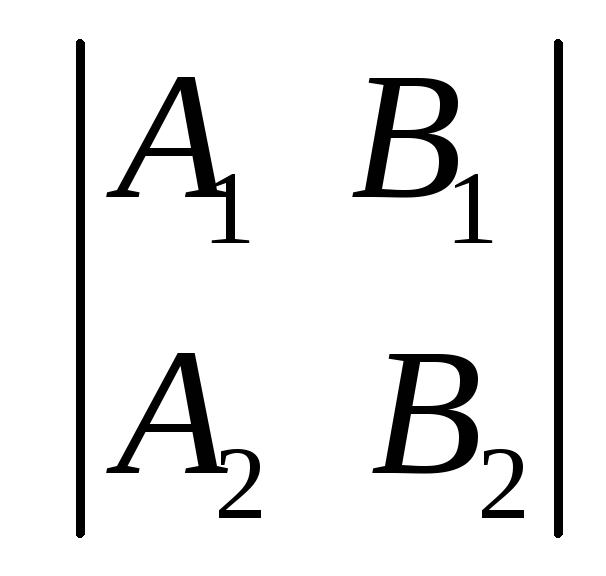отличен от нуля. Для определенности будем считать, что. Тогда, взяв произвольное значение, получим систему уравнений относительно неизвестныхи:

.

По теореме Крамера эта система имеет единственное решение, определяемое формулами

, . (3.19)

Если взять , то прямая, задаваемая уравнениями (3.17), проходит через точку.

Таким образом, для случая, когда , канонические уравнения прямой (3.17) имеют вид

.

Аналогично записываются канонические уравнения прямой (3.17) для случая, когда отличен от нуля определитель 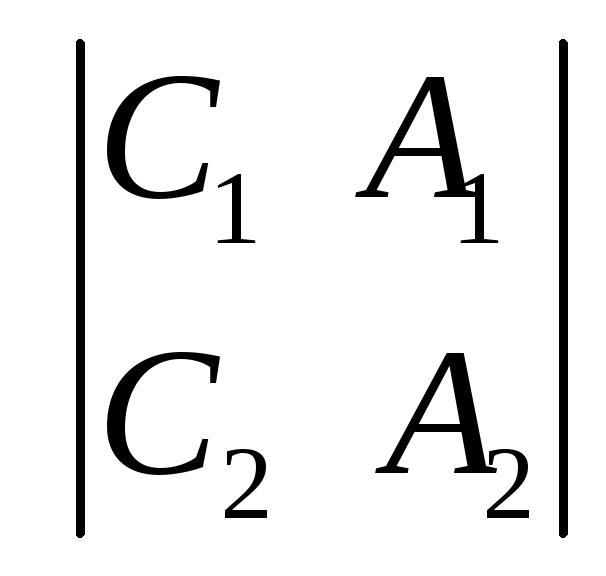или.

Если прямая проходит через две различные точки и, то ее канонические уравнения имеют вид

. (3.20)

Это следует из того, что прямая проходит через точку и имеет направляющий вектор.

Рассмотрим канонические уравнения (3.18) прямой. Примем каждое из отношений за параметр , т. е.. Один из знаменателей этих дробей отличен от нуля, а соответствующий числитель может принимать любые значения, поэтому параметрможет принимать любые вещественные значения. Учитывая, что каждое из отношений равно, получимпараметрические уравнения прямой:

, ,. (3.21)

Пусть плоскость задана общим уравнением, а прямая параметрическими уравнениями ,,. Точкапересечения прямойи плоскостидолжна одновременно принадлежать плоскости и прямой. Это возможно только в том случае, когда параметрудовлетворяет уравнению, т. е.. Таким образом, точка пересечения прямой и плоскости имеет координаты

,

,

.

П р и м е р 32. Составить параметрические уравнения прямой, проходящей через точки и.

Решение. За направляющий вектор прямой возьмем вектор . Прямая проходит через точку, поэтому по формуле (3.21) искомые уравнения прямой имеют вид,,.

П р и м е р 33. Вершины треугольника имеют координаты,исоответственно. Составить параметрические уравнения медианы, проведенной из вершины.

Решение. Пусть  середина стороны , тогда,,. В качестве направляющего вектора медианы возьмем вектор. Тогда параметрические уравнения медианы имеют вид,,.

П р и м е р 34. Составить канонические уравнения прямой, проходящей через точку параллельно прямой.

Решение. Прямая задана как линия пересечения плоскостей с нормальными векторами и. В качестве направляющего вектораэтой прямой возьмем вектор, т. е.. Согласно (3.18) искомое уравнение имеет видили.

3.8. Угол между прямыми в пространстве. Угол между прямой и плоскостью

Пусть две прямые ив пространстве заданы своими каноническими уравнениямии. Тогда один из угловмежду этими прямыми равен углу между их направляющими векторамии. Воспользовавшись формулой (2.22), для определения углаполучим формулу

. (3.22)

Второй угол между этими прямыми равени.

Условие параллельности прямых иравносильно условию коллинеарности векторовии заключается в пропорциональности их координат, т. е. условие параллельности прямых имеет вид

. (3.23)

Если прямые иперпендикулярны, то их направляющие векторы ортогональны, т.е. условие перпендикулярности определяется равенством

. (3.24)

Рассмотрим плоскость , заданную общим уравнением, и прямую, заданную каноническими уравнениями.

L

Угол между прямойи плоскостьюявляется дополнительным к углумежду направляющим вектором прямой и нормальным вектором плоскости, т. е.и, или

. (3.24)

Условие параллельности прямой и плоскостиэквивалентно условию перпендикулярности направляющего вектора прямой и нормального вектора плоскости, т. е. скалярное произведение этих векторов должно равняться нулю:

. (3.25)

Если же прямая перпендикулярна плоскости, то направляющий вектор прямой и нормальный вектор плоскости должны быть коллинеарны. В этом случае координаты векторов пропорциональны, т. е.

. (3.26)

П р и м е р 35. Найти тупой угол между прямыми ,,и,,.

Решение. Направляющие векторы этих прямых имеют координаты и. Поэтому один уголмежду прямыми определяется соотношением, т. е.. Поэтому условию задачи удовлетворяет второй угол между прямыми, равный.

3.9. Расстояние от точки до прямой в пространстве

Пусть  точка пространства с координатами , прямая, заданная каноническими уравнениями . Найдем расстояниеот точкидо прямой.

d

L

Приложим направляющий вектор к точке. Расстояниеот точкидо прямойявляется высотой параллелограмма, построенного на векторахи. Найдем площадь параллелограмма, используя векторное произведение:

.

С другой стороны, . Из равенства правых частей двух последних соотношений следует, что

. (3.27)

3.10. Эллипсоид

Определение. Эллипсоидом называется поверхность второго порядка, которая в некоторой системе координат определяется уравнением

. (3.28)

Уравнение (3.28) называется каноническим уравнением эллипсоида.

Из уравнения (3.28) следует, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат  центром симметрии. Числа называются полуосями эллипсоида и представляют собой длины отрезков от начала координат до пересечения эллипсоида с осями координат. Эллипсоид представляет собой ограниченную поверхность, заключенную в параллелепипеде,,.

Установим геометрический вид эллипсоида. Для этого выясним форму линий пересечения его плоскостями, параллельными координатным осям.

Для определенности рассмотрим линии пересечения эллипсоида с плоскостями , параллельными плоскости. Уравнение проекции линии пересечения на плоскостьполучается из (3.28), если в нем положить. Уравнение этой проекции имеет вид

. (3.29)

Если , то (3.29) является уравнением мнимого эллипса и точек пересечения эллипсоида с плоскостьюнет. Отсюда и следует, что. Если, то линия (3.29) вырождается в точки, т. е. плоскостикасаются эллипсоида в точкахи. Если, тои можно ввести обозначения

, . (3.30)

Тогда уравнение (3.29) принимает вид

, (3.31)

т. е. проекция на плоскость линии пересечения эллипсоида и плоскостипредставляет собой эллипс с полуосями, которые определяются равенствами (3.30). Так как линия пересечения поверхности плоскостями, параллельными координатным, представляет собой проекцию, «поднятую» на высоту, то и сама линия пересечения является эллипсом.

П

z

ри уменьшении значенияполуосииувеличиваются и достигают своего наибольшего значения при, т. е. в сечении эллипсоида координатной плоскостьюполучается самый большой эллипс с полуосямии.

y

O

x

Представление об эллипсоиде можно получить и другим образом. Рассмотрим на плоскости семейство эллипсов (3.31) с полуосямии, определяемыми соотношениями (3.30) и зависящими от. Каждый такой эллипс является линией уровня, т. е. линией, в каждой точке которой значениеодинаково. «Подняв» каждый такой эллипс на высоту, получим пространственный вид эллипсоида.

Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям и.

Таким образом, эллипсоид представляет собой замкнутую эллиптическую поверхность. В случае эллипсоид является сферой.

Линия пересечения эллипсоида с любой плоскостью является эллипсом, так как такая линия представляет собой ограниченную линию второго порядка, а единственная ограниченная линия второго порядка  эллипс.