
Уравнение (1.33) называется каноническим уравнением гиперболы.
Гипербола симметрична относительно осей координат и относительно начала координат. Оси симметрии гиперболы называются ее осями, а центр симметрии центром гиперболы.
Рассмотрим
часть гиперболы, расположенной в I
четверти координатной плоскости. Пусть
точка
![]() принадлежит гиперболе. На прямой
принадлежит гиперболе. На прямой![]() возьмем точку
возьмем точку![]() .
Тогда
.
Тогда![]() и
и![]() =
=![]() =
=![]() при
при![]() .
Поэтому прямые
.
Поэтому прямые![]() являются асимптотами гиперболы.
являются асимптотами гиперболы.
y
В1 В2
b а
![]()
![]() O
A2
O
A2
![]() x
x
С1 С2
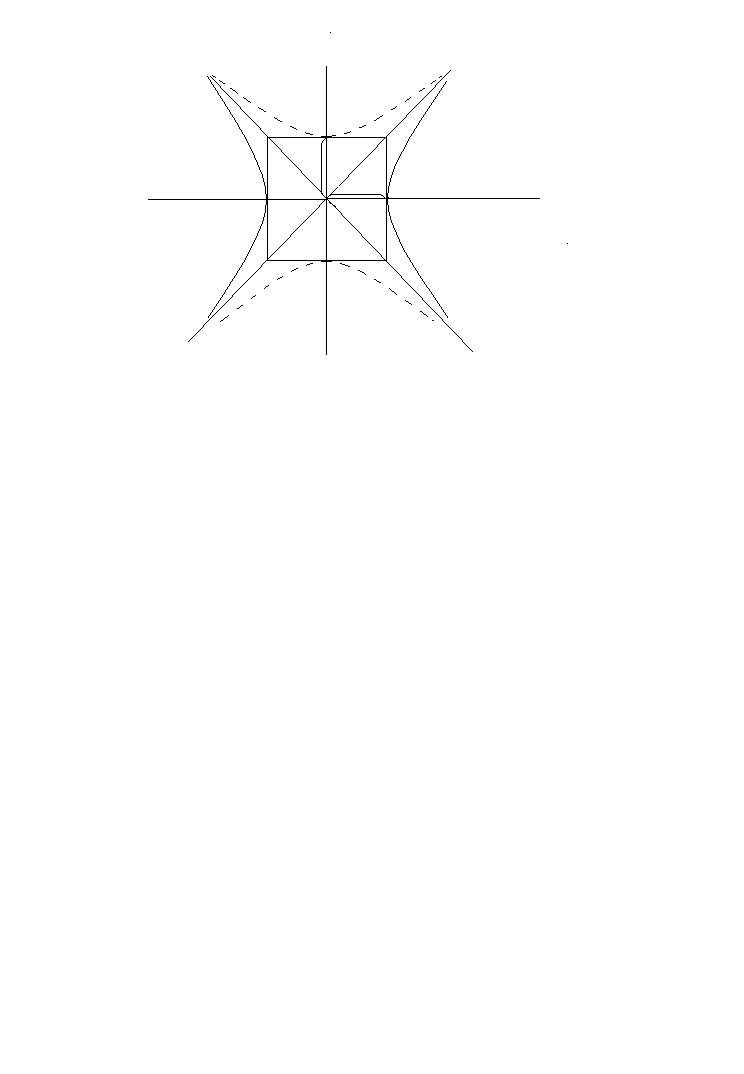
Точки
![]() и
и![]() пересечения гиперболы с осью
пересечения гиперболы с осью![]() называются ее вершинами, ось
называются ее вершинами, ось![]()
ее действительной осью, прямоугольник
ее действительной осью, прямоугольник
![]()
основным прямоугольником гиперболы,
основным прямоугольником гиперболы,
![]() и
и![]()
соответственно действительной и мнимой
полуосями.
соответственно действительной и мнимой
полуосями.
У
гиперболы различают правую и левую
ветви, расположенные в полуплоскостях
![]() и
и![]() соответственно.
соответственно.
Уравнение
![]() также определяет гиперболу, которая
изображена на рисунке пунктирной линией.
Эта гипербола называется сопряженной
к гиперболе
также определяет гиперболу, которая
изображена на рисунке пунктирной линией.
Эта гипербола называется сопряженной
к гиперболе![]() и имеет такие же асимптоты.
и имеет такие же асимптоты.
Гипербола
с равными полуосями (![]() )
называется равносторонней, и ее
каноническое уравнение имеет вид
)
называется равносторонней, и ее
каноническое уравнение имеет вид![]() (
(![]() ).
Ее основным прямоугольником является
квадрат, а асимптоты взаимно перпендикулярны.
).
Ее основным прямоугольником является
квадрат, а асимптоты взаимно перпендикулярны.
Определение.
Эксцентриситетом гиперболы
![]() называется отношение
называется отношение![]() ,
где
,
где![]()
половина расстояния между фокусами,
половина расстояния между фокусами,
![]()
действительная полуось, т. е.
действительная полуось, т. е.
![]() .
(1.34)
.
(1.34)
Так
как
![]()
![]() ,
то
,
то![]() .
Если
.
Если![]() ,
то
,
то![]() .
Если
.
Если![]() ,
то
,
то![]() .
Эксцентриситет гиперболы характеризует
форму ее основного прямоугольника, т.
е. и саму гиперболу.
.
Эксцентриситет гиперболы характеризует
форму ее основного прямоугольника, т.
е. и саму гиперболу.
П
р и м е р 17. Составить
уравнение гиперболы, фокусы которой
расположены на оси ординат симметрично
относительно начала координат, если
расстояние между фокусами
![]() и эксцентриситет
и эксцентриситет![]() .
.
Решение.
Так как расстояние между фокусами
![]() ,
то
,
то![]() и фокусы, расположенные на оси ординат,
имеют координаты
и фокусы, расположенные на оси ординат,
имеют координаты![]() и
и![]() .
Вещественной полуосью гиперболы является
.
Вещественной полуосью гиперболы является![]() .
Учитывая, что эксцентриситет гиперболы
равен отношению
.
Учитывая, что эксцентриситет гиперболы
равен отношению![]() к вещественной полуоси, находим
к вещественной полуоси, находим![]() .
Тогда
.
Тогда![]() .
Искомое уравнение гиперболы имеет вид
.
Искомое уравнение гиперболы имеет вид![]() .
.
1.14. Директрисы эллипса и гиперболы
Определение.
Две прямые, перпендикулярные большой
оси эллипса и расположенные симметрично
относительно центра на расстоянии
![]() от него, называются директрисами
эллипса, т. е. директрисы
эллипса задаются уравнениями
от него, называются директрисами
эллипса, т. е. директрисы
эллипса задаются уравнениями
![]() (
(![]() ).
).
у
d![]()





![]()
с
![]()

х
О
![]()

![]()
![]()


![]()
![]()
a
Теорема
5. Если
![]()
расстояние произвольной точки
расстояние произвольной точки
![]() эллипса до какого-либо фокуса, а
эллипса до какого-либо фокуса, а![]()
расстояние той же точки до соответствующей
этому фокусу директрисы, то отношение
расстояние той же точки до соответствующей
этому фокусу директрисы, то отношение
![]() есть величина постоянная, равная
эксцентриситету эллипса.
есть величина постоянная, равная
эксцентриситету эллипса.
Доказательство.
Пусть
![]()
точка правой директрисы эллипса, тогда
точка правой директрисы эллипса, тогда
![]() .
Расстояние
.
Расстояние![]() точки
точки![]() до соответствующего фокуса
до соответствующего фокуса![]() :
:
![]() .
Таким образом,
.
Таким образом,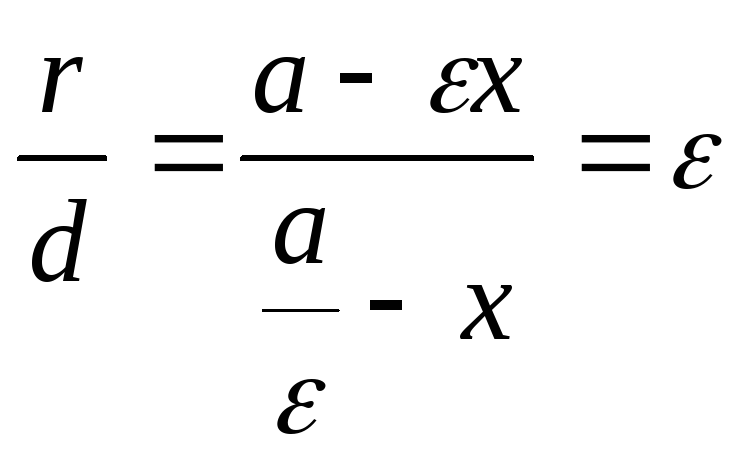 ,
теорема доказана.
,
теорема доказана.
Определение.
Две прямые, перпендикулярные действительной
оси гиперболы и расположенные симметрично
относительно центра на расстоянии
![]() от него, называются директрисами
гиперболы, т. е.
директрисы гиперболы задаются уравнениями
от него, называются директрисами
гиперболы, т. е.
директрисы гиперболы задаются уравнениями
![]() (
(![]() ),
где
),
где![]()
вещественная полуось,
вещественная полуось,
![]()
эксцентриситет гиперболы.
эксцентриситет гиперболы.
Теорема
6. Если
![]()
расстояние произвольной точки
расстояние произвольной точки
![]() гиперболы
гиперболы![]() до какого-либо фокуса, а
до какого-либо фокуса, а![]()
расстояние той же точки до соответствующей
этому фокусу директрисы, то отношение
расстояние той же точки до соответствующей
этому фокусу директрисы, то отношение
![]() есть величина постоянная, равная
эксцентриситету гиперболы.
есть величина постоянная, равная
эксцентриситету гиперболы.
Доказательство.
Пусть
![]()
точка правой директрисы гиперболы,
тогда
точка правой директрисы гиперболы,
тогда
![]() ,
так как
,
так как![]() ,
,![]() .
Расстояние
.
Расстояние![]() точки
точки![]() до соответствующего фокуса
до соответствующего фокуса![]() :
:![]()
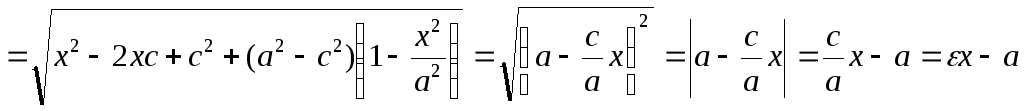 .
Получили, что
.
Получили, что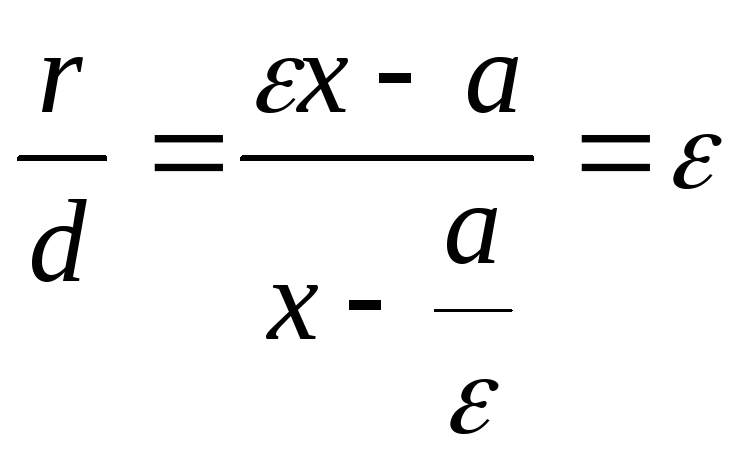 .
Теорема доказана.
.
Теорема доказана.
На основании доказанных теорем можно дать следующее определение эллипса и гиперболы.
Определение.
Множество точек
плоскости, для которых отношение
расстояний до фокуса и до соответствующей
фокусу директрисы является постоянной
величиной, равной
![]() ,
есть эллипс, если
,
есть эллипс, если![]() ,
и гипербола, если
,
и гипербола, если![]() .
.
П
р и м е р 18. Составить
уравнение эллипса, фокусы которого
расположены на оси абсцисс симметрично
относительно начала координат, если
дана точка
![]() эллипса и расстояние между его директрисами
равно 10.
эллипса и расстояние между его директрисами
равно 10.
Решение.
Для того чтобы составить уравнение
заданного эллипса, надо найти его
полуоси. Координаты точки
![]() удовлетворяют уравнению эллипса, поэтому
удовлетворяют уравнению эллипса, поэтому![]() .
Фокусы эллипса расположены на оси
абсцисс, вследствие чего расстояние
.
Фокусы эллипса расположены на оси
абсцисс, вследствие чего расстояние![]() между директрисами определяется по
формуле
между директрисами определяется по
формуле![]() .
Поэтому
.
Поэтому![]() ,
или
,
или![]() .
Так как
.
Так как![]() ,
то уравнение относительно
,
то уравнение относительно![]() принимает вид
принимает вид![]() ,
т. е.
,
т. е.![]() и соответственно
и соответственно![]() .
Таким образом, искомое уравнение эллипса
.
Таким образом, искомое уравнение эллипса![]() .
.
П
р и м е р 19.
Эксцентриситет гиперболы
![]() ,
расстояние
,
расстояние![]() от точки
от точки![]() гиперболы до директрисы равно 4. Вычислить
расстояние
гиперболы до директрисы равно 4. Вычислить
расстояние![]() от точки
от точки![]() до фокуса, одностороннего с этой
директрисой.
до фокуса, одностороннего с этой
директрисой.
Решение.
По определению
гиперболы
![]() ,
поэтому
,
поэтому![]() .
.
1.15. Парабола
Определение.
Параболой
называется множество всех точек
плоскости, каждая из которых находится
на одинаковом расстоянии от данной
точки, называемой фокусом, и от данной
прямой, называемой директрисой и не
проходящей через фокус, т. е.
![]() .
.
Выберем прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус перпендикулярно директрисе. Положительное направление оси от директрисы к фокусу. Начало системы координат находится на одинаковом расстоянии от фокуса и директрисы.
y

d
![]()
![]()


r
x
O
![]()

Пусть
![]()
произвольная
точка плоскости;
произвольная
точка плоскости;
![]()
расстояние точки
расстояние точки
![]() до директрисы;
до директрисы;![]()
расстояние от фокуса до директрисы.
Тогда директриса задается уравнением
расстояние от фокуса до директрисы.
Тогда директриса задается уравнением
![]() ,
фокус
,
фокус![]() имеет координаты
имеет координаты![]() и
и![]() ,
,![]() .
Согласно определению параболы
.
Согласно определению параболы![]() или
или![]() .
Из последнего равенства получаем
.
Из последнего равенства получаем
![]() .
(1.35)
.
(1.35)
Уравнение (1.35) называется каноническим уравнением параболы.
Покажем,
что любая точка
![]() ,
координаты которой удовлетворяют
уравнению (1.35), является точкой гиперболы.
,
координаты которой удовлетворяют
уравнению (1.35), является точкой гиперболы.
Координаты
точки
![]() удовлетворяют уравнению (1.35), поэтому
удовлетворяют уравнению (1.35), поэтому![]() и расстояние
и расстояние![]() этой точки до прямой
этой точки до прямой![]() :
:![]() .
Расстояние
.
Расстояние![]() точки
точки![]() до фокуса
до фокуса![]() :
:![]()
![]() ,
т. е. точка
,
т. е. точка![]() является точкой гиперболы.
является точкой гиперболы.
Уравнение (1.35) это уравнение второй степени, поэтому парабола кривая второго порядка.
Парабола
симметрична относительно оси
![]() и проходит через точку
и проходит через точку![]() .
Точка
.
Точка![]() называется вершиной параболы, ось
симметрии (ось
называется вершиной параболы, ось
симметрии (ось![]() )
ее осью симметрии, а расстояние
)
ее осью симметрии, а расстояние
![]() от фокуса до директрисы
параметром.
от фокуса до директрисы
параметром.
Рассмотрим
![]() .
На параболе имеются две точки с абсциссой
.
На параболе имеются две точки с абсциссой![]() :
:![]() и
и![]() .
Эти точки находятся на расстоянии
.
Эти точки находятся на расстоянии![]() друг от друга, т. е. чем больше параметр
друг от друга, т. е. чем больше параметр![]() ,
тем шире область, лежащая внутри параболы.
,
тем шире область, лежащая внутри параболы.
Если система координат выбрана таким образом, что ось абсцисс совмещена с осью параболы, а начало координат с вершиной, но ось Ox направлена от фокуса к директрисе, то уравнение параболы записывается в виде
![]() .
(1.36)
.
(1.36)

y
![]()
F
O
![]() x
x
Если начало координат совмещено с вершиной параболы, а ее ось с осью ординат, то уравнение параболы имеет вид
![]() (1.37)
(1.37)
и парабола лежит в верхней полуплоскости. Если же парабола расположена в нижней полуплоскости, то она задается уравнением
![]() .
(1.38)
.
(1.38)
Каждое из уравнений (1.36) (1.38), как и уравнение (1.35), называется каноническим уравнением параболы.
П р и м е р 20.
Составить уравнение параболы, вершина
которой находится в начале координат,
зная, что парабола расположена симметрично
относительно оси
![]() и проходит через точку
и проходит через точку![]() .
.
Решение.
Осью параболы является ось ординат,
поэтому уравнение имеет вид, определяемый
уравнением (1.37) или (1.38). Точка
![]() расположена в верхней полуплоскости,
поэтому
расположена в верхней полуплоскости,
поэтому![]() ,
и значение параметра
,
и значение параметра![]() находится из уравнения
находится из уравнения![]() .
Таким образом,
.
Таким образом,![]() ,
и искомое уравнение имеет вид
,
и искомое уравнение имеет вид![]() .
.
П р и м е р 21.
Составить уравнение параболы, если даны
ее фокус
![]() и директриса
и директриса![]() .
.
Решение.
По формуле (1.15) расстояние
![]() от фокуса до директрисы
от фокуса до директрисы![]() ,
поэтому параметр параболы
,
поэтому параметр параболы![]() .
Прямая, проходящая через фокус
перпендикулярно директрисе, задается
уравнением
.
Прямая, проходящая через фокус
перпендикулярно директрисе, задается
уравнением![]() и является осью симметрии параболы.
Вершина параболы расположена на ее оси
на одинаковом расстоянии от фокуса и
директрисы, т. е. имеет координаты
и является осью симметрии параболы.
Вершина параболы расположена на ее оси
на одинаковом расстоянии от фокуса и
директрисы, т. е. имеет координаты![]() .
Положительное направление от директрисы
к фокусу совпадает с положительным
направлением оси
.
Положительное направление от директрисы
к фокусу совпадает с положительным
направлением оси![]() .
Таким образом, искомое уравнение имеет
вид
.
Таким образом, искомое уравнение имеет
вид![]() или
или![]() .
.
