1.16. Общее уравнение линии второго порядка

Общее уравнение линии второго порядка имеет вид

, (1.39)

где ,.

Лемма. Пусть в прямоугольной системе координат задано уравнение (1.39) и. Тогда с помощью параллельного сдвига и последующего поворота осей на некоторый угол уравнение (1.39) приводится к виду:

, (1.40)

где , координаты точек в новой системе координат.

Доказательство. Параллельным переносом сдвинем начало координат в точку. Тогда,. В новой системе координатуравнение (1.39) примет вид

, или

, (1.41)

где ,,. В уравнении (1.41) коэффициентыиобращаются в нуль, если подобрать,так, чтобы

(1.42)

По теореме Крамера система (1.42) имеет единственное решение, так как :,. Уравнения (1.42) называются уравнениями центра линий второго порядка, а точка центром этой линии. При параллельном сдвиге начала прямоугольной системы координат в точку уравнение (1.41) принимает вид

. (1.43)

Пусть  прямоугольная система координат, полученная поворотом на угол системы. Координаты точек плоскости в этом случае преобразуются по формулам (1.17):

, .

Уравнение (1.43) в прямоугольной системе координат принимает вид, или

, (1.44)

где ,,.

Выберем угол таким образом, чтобы коэффициентбыл равен нулю, т. е., или

. (1.45)

Если , то, и можно взять. Если, то из уравнения (1.45), и поэтому существует угол, при котором выполняется условие (1.45). При повороте осей координат на соответствующий уголуравнение (1.44) приводится к виду (1.40). Лемма доказана.

Коэффициенты не меняются при параллельном переносе системы координат, но изменяются при повороте осей. Легко проверить, что выражениеявляется инвариантом общего уравнения линий второго порядка, т. е. не меняется при повороте осей. В зависимости от выражения() выделяют три типа линий второго порядка:

1. эллиптический ();

2. гиперболический ();

3. параболический ().

Рассмотрим линии второго порядка эллиптического типа. Так как для эллиптического типа , то в некоторой системе координат общее уравнение может быть приведено к виду

. (1.46)

Возможны три случая:

1. если ,, то,, поэтому можно ввести обозначения,, с использованием которых уравнение (1.46) приводится к уравнению (1.30) эллипса:

;

2. если ,, то из (1.46) получаем уравнение, разделив обе части которого на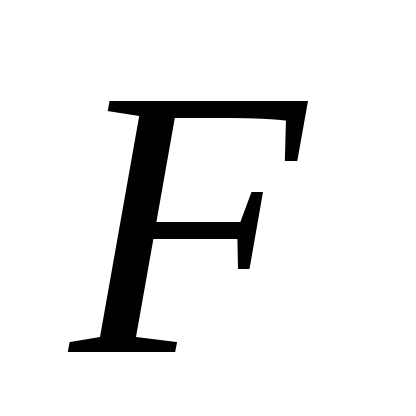и обозначив,, получим уравнение мнимого эллипса:

; (1.47)

3. если ,, то, сделав замену,(,) или,(,), приведем уравнение (1.46) к уравнению пары мнимых пересекающихся прямых:

. (1.48)

Уравнение линии второго порядка гиперболического типа в некоторой системе координат также может быть приведено к виду (1.46), так как :

1. если ,,или,,, то соответствующей заменой (например, для случая,,можно сделать замену,) уравнение (1.46) приводится к уравнению (1.33) гиперболы:

;

2. если ,,или,,, то, положив,(,), получим уравнение пары пересекающихся вещественных прямых

. (1.49)

Уравнения линий второго порядка параболического типа не могут быть приведены к уравнению вида (1.46), но с помощью поворота осей на угол , указанный в лемме, их можно привести к виду

. (1.50)

Коэффициенты уравнения линии второго порядка параболического типа удовлетворяют условию . В уравнении (1.50), следовательно,. Пусть, тогда(если, то уравнение линии становится уравнением первого порядка). Уравнение (1.50) принимает вид, или

. (1.51)

Параллельным переносом переместим начало координат в точку . Уравнение (1.51) в новой системе координатпримет вид

, (1.52)

где ,,.

1. Если , то уравнение (1.52) приводится к уравнению. В прямоугольной системе координат, полученной изпараллельным переносом начала координат в точку,,и уравнение (1.52) принимает вид. Если, то, обозначив(), получим уравнение (1.35) параболы:

.

2. Если , то уравнение (1.52) имеет вид. Введем обозначение. Тогда приполучим уравнение пары вещественных параллельных прямых

. (1.53)

Если , то будет пара мнимых параллельных прямых, задаваемых уравнением.

При получим пару совпадающих прямых, задаваемых уравнением.

Замечание. В случае, когда ,уравнение (1.50) линии второго порядка параболического типа также приводится к каноническим уравнениям параболы, пары мнимых параллельных прямых, пары параллельных прямых или пары совпадающих прямых.

Используя вспомогательную лемму и различные типы линий второго порядка, доказали теорему.

Теорема 7. Пусть в прямоугольной системе координат задано общее уравнение линии второго порядка . Тогда существует такая прямоугольная система координат, в которой это уравнение принимает один из следующих канонических видов:

1. эллипс;

2. мнимый эллипс;

3. –пара мнимых пересекающихся прямых;

4. –гипербола;

5. –пара пересекающихся прямых;

6. –парабола;

7. –пара параллельных прямых;

8. –пара мнимых параллельных прямых;

9. –пара совпадающих прямых.