20-12-2012_21-26-59 / геом 36-45

Определение. Единичный вектор, имеющий одинаковое направление с вектором , называется ортом вектора и обозначается обычно символом .

Линейными операциями над векторами принято называть операцию сложения векторов и операцию умножения векторов на вещественные числа.

Определение. Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец  с концом вектора при условии, что вектор приложен к концу вектора .

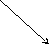
Этот способ сложения векторов называется правилом треугольника. Операция сложения векторов обладает следующими свойствами.

1. .

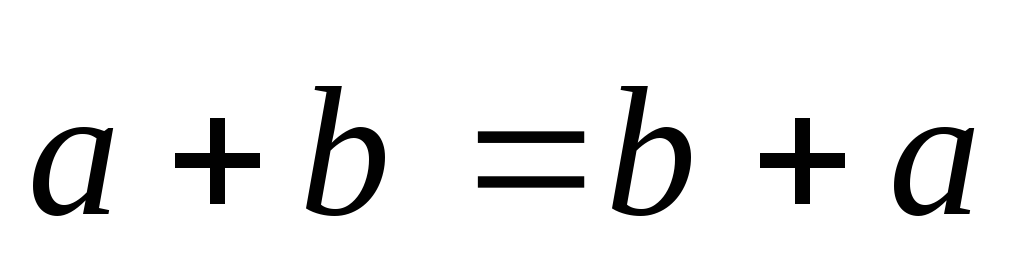Д

B

оказательство. Приложим два произвольных вектора и к общему началу . Обозначим концы векторов и буквами и соответственно и рассмотрим параллелограмм . Из равенства векторов следует, что , . Из треугольника следует, что диагональ рассматриваемого параллелограмма равна , из треугольника получаем, что диагональ равна . Таким образом, . Свойство доказано.

О

C

A

2. .

Д

B

оказательство. Для доказательства этого свойства приложим вектор к произвольной точке , вектор  к концу вектора , а начало вектора совместим с концом вектора .

A

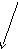
C

О

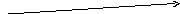
Обозначим буквами , и концы векторов , и соответственно и рассмотрим четырехугольник .

Тогда , , т. е. . Свойство доказано.

3. Существует нулевой вектор такой, что для любого вектора выполняется равенство .

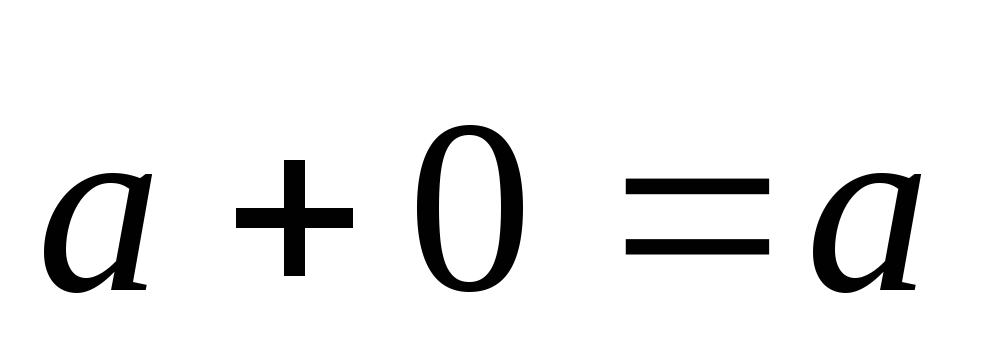Доказательство. Обозначим буквами и соответственно начало и конец вектора , т. е. . Приложим начало нулевого вектора к концу вектора , тогда . По определению суммы векторов . Свойство доказано.

4. Для каждого вектора существует противоположный ему вектор такой, что .

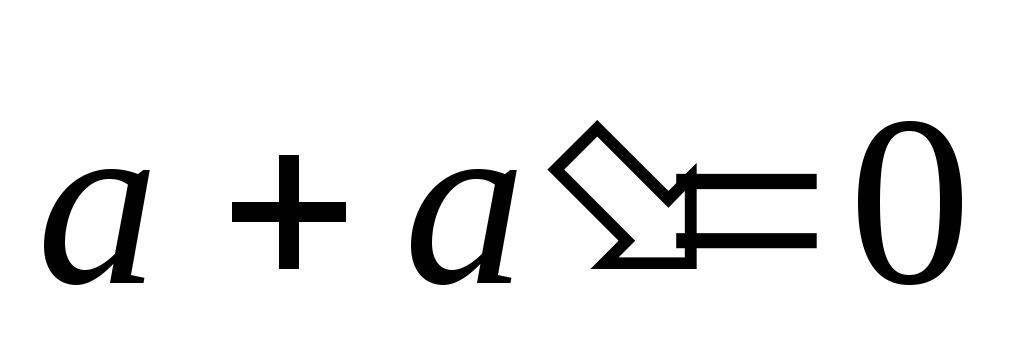Доказательство. Определим вектор как вектор, коллинеарный вектору , имеющий с вектором одинаковую длину и противоположное направление. Обозначим буквами и соответственно начало и конец вектора , т. е. . Приложим начало вектора к концу вектора , тогда . По определению суммы векторов . Свойство доказано.

Доказательство свойства 1 позволяет вывести правило параллелограмма для сложения двух векторов: если векторы и приложены к общему началу и на них, как на смежных сторонах, построен параллелограмм, то сумма (или ) этих векторов представляет собой диагональ построенного параллелограмма, идущую из общего начала векторов и .

Если векторы и коллинеарны, то параллелограмм, построенный на этих векторах, как на сторонах, вырождается в отрезок, поэтому понятие диагонали параллелограмма теряет смысл, и сложение векторов осуществляется по правилу треугольника.

Доказанные свойства операции сложения векторов совпадают со свойствами операции сложения действительных чисел. Поэтому правило сложения можно распространить на сумму любого конечного числа векторов. Сумма любого числа векторов может быть построена по правилу многоугольника: чтобы сложить несколько векторов , , …, , надо вектор () приложить к концу вектора , тогда суммой векторов будет вектор, соединяющий начало вектора с концом вектора .

Если  начало вектора ,  конец вектора (), то вектор замыкает ломаную до многоугольника, поэтому правило сложения векторов по правилу многоугольника иногда называют правилом замыкания ломаной до многоугольника.

Определение. Разностью векторов и называется вектор , который в сумме с вектором дает вектор .

Покажем, что вектор равен сумме векторов и , где  вектор, противоположный вектору . Действительно, если , то по свойствам 2  4 операции сложения векторов имеем: , т. е. вектор равен разности векторов и .

Из определения разности и правила треугольника сложения векторов следует правило построения разности : разность приведенных к общему началу двух векторов и представляет собой вектор, идущий из конца вычитаемого вектора к концу уменьшаемого вектора .

Определение. Произведением вектора на вещественное число называется вектор, коллинеарный вектору , имеющий длину и направление, совпадающее с направлением вектора в случае и противоположное направлению вектора в случае . Если или , то произведение равно нулевому вектору, направление которого не определено.

Таким образом, при умножении вектора на число происходит его «растяжение» в раз, т. е. он либо растягивается в раз (), либо сжимается в раз (), либо кроме растяжения () и сжатия () происходит изменение направления вектора.

Свойства операция умножения вектора на вещественное число:

1. Распределительное свойство числового сомножителя относительно суммы векторов: .

Доказательство. Приложим векторы и к общему началу и на них, как на смежных сторонах, построим параллелограмм, диагональ которого будет равна .

О

При «растяжении» сторон этого параллелограмма в раз в силу свойств подобия диагональ также «растягивается» в раз. Это означает, что . Свойство доказано.

2. Распределительное свойство векторного сомножителя относительно суммы чисел: .

Доказательство. Если , то по определению умножения вектора на число , , и, следовательно, .

Если или , то справедливость равенства следует из свойств вещественных чисел и определения умножения вектора на число.

Пусть числа и имеют одинаковые знаки и . Тогда векторы , и (соответственно и векторы , ) коллинеарные и одинаково направлены. Поэтому . Если числа и имеют одинаковые знаки, то , поэтому . Таким образом, векторы и коллинеарные, одинаково направлены и имеют равные длины, следовательно, они равны.

Пусть числа и имеют разные знаки и . Для определенности будем считать, что . В этом случае векторы и направлены так же, как и вектор . Длина вектора равна , а для вектора имеем: , т. е. длины векторов и равны. Так как эти векторы коллинеарные, направлены в одну сторону и имеют одинаковые длины, то они равны.

Если , то обе части доказываемого равенства равны нулю, следовательно, . Свойство доказано.

3. Сочетательное свойство числовых сомножителей: .

Доказательство. Если или , равенство верно, так как обе части равенства обращаются в нуль. Если , , , то направления векторов и либо совпадают с направлением вектора (если ), либо противоположны направлению вектора (если ), т. е. векторы и одинаково направлены. Кроме того, они имеют одинаковые длины: и . Следовательно, векторы и равны. Свойство доказано.

2.3. Проекции векторов

Пусть в пространстве задана некоторая ось и вектор . Через точки и проведем плоскости, перпендикулярные прямой . Обозначим точки пересечения прямой и построенных плоскостей и .

Определение. Проекцией вектора на ось называется величина направленного отрезка на оси , т. е.

. (2.1)

Если направление совпадает с направлением оси , то , если же направления вектора и оси противоположны, то .

Теорема 1. Проекция вектора на ось равна длине вектора , умноженной на косинус угла между вектором и осью , т. е.

, (2.2)

где  угол между вектором и осью .

Доказательство. Если , то при проекции вектора на ось вектор является нулевым, поэтому условие (2.2) выполняется.

Если , то в силу (2.1) .