Доказательство. Если векторы компланарны, то, согласно доказанной теореме, их смешанное произведение равно нулю. Если смешанное произведение векторов равно нулю, то по этой же теореме проекция одного из векторов на ось, определяемую векторным произведением двух других векторов, равна нулю, т. е. он параллелен плоскости, в которой лежат два другие вектора. Это означает, что векторы компланарны. Следствие доказано.

Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.

Доказательство. Если два вектора из трех совпадают, то такие три вектора компланарны и их смешанное произведение равно нулю. Следствие доказано.

Теорема 14. Если векторы ,изаданы своими координатами, т. е.,,, то смешанное произведение векторов,ивычисляется по формуле

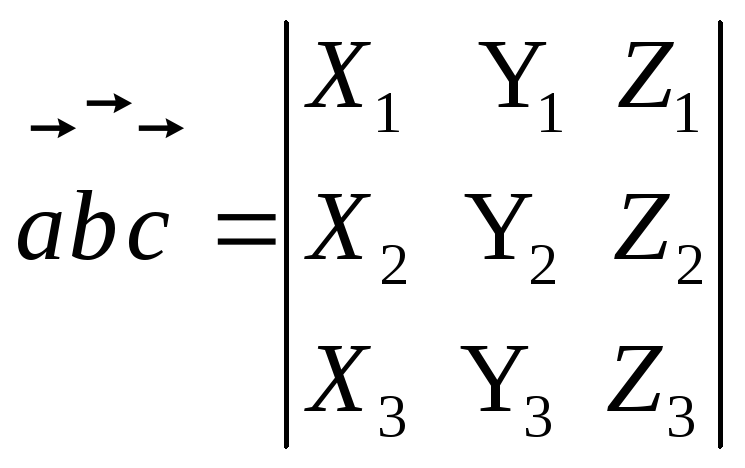. (2.34)

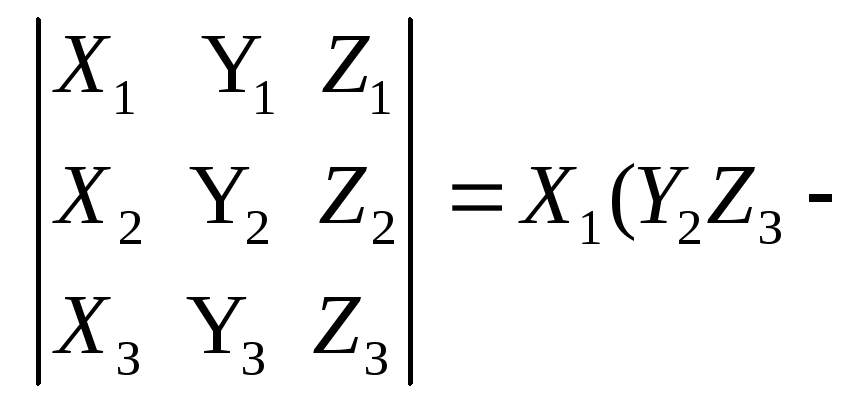
Доказательство. Разложим определитель, стоящий в правой части выражения (2.34), по первой строке. Получим: . Теорема доказана.

Теорема 15. Пусть даны точки ,,,. Тогда объем параллелепипеда, построенного на векторах,икак на сторонах, вычисляется по формуле

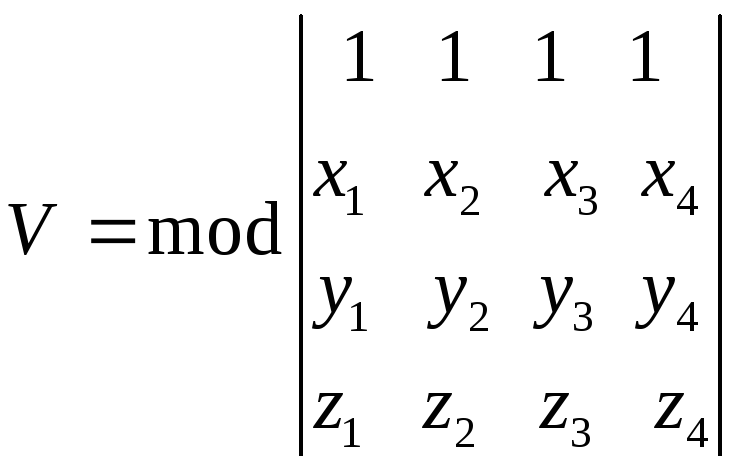. (2.35)

Доказательство. Преобразуем правую часть (2.35), используя свойства определителей:

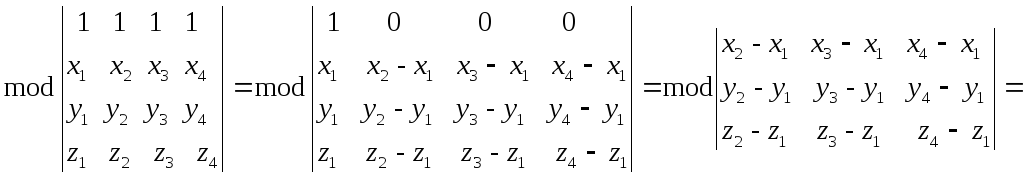
. Теорема доказана.

Следствие. Объем треугольной пирамиды с вершинами в точках ,,,вычисляется по формуле

. (2.36)

Доказательство. Если четыре вершины параллелепипеда, не лежащие в одной плоскости, являются вершинами треугольной пирамиды, то объем пирамиды составляет объема параллелепипеда. Учитывая, что объем параллелепипеда вычисляется по формуле (2.35), получаем доказываемое тождество. Следствие доказано.

П р и м е р 29. Вершины тетраэдра находятся в точках ,,и. Найти длину высотытетраэдра, опущенной из вершины.

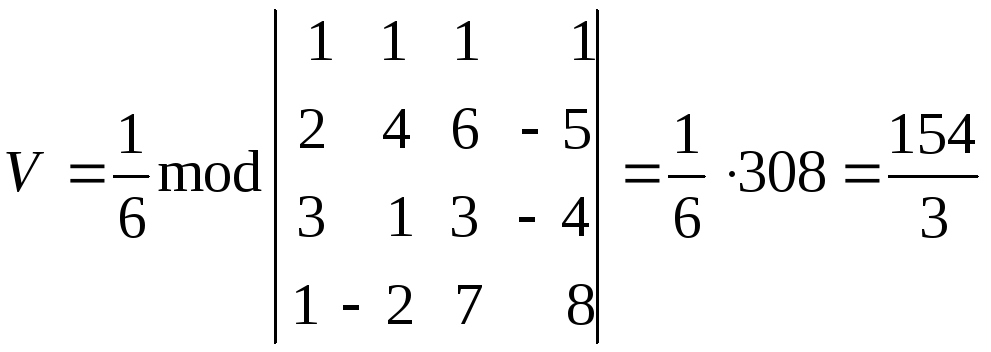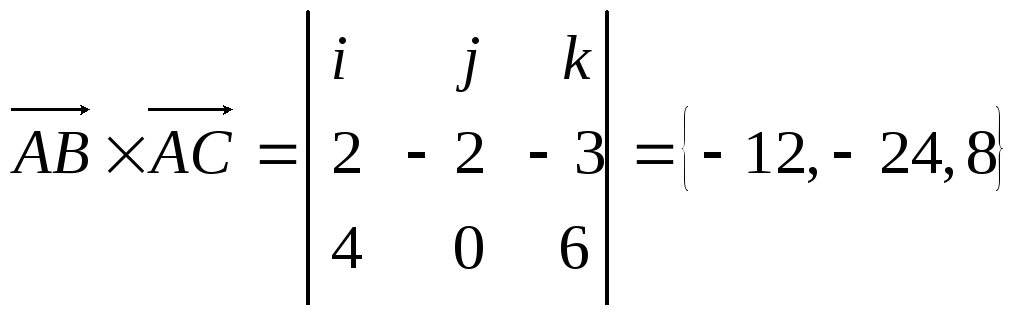Решение. Так как объем тетраэдра и его высотасвязаны соотношением, где площадь грани , то. Объемтетраэдра и площадьгранинайдем, используя векторное и смешанное произведения векторов. По формуле (2.36) имеем:. Из определения векторного произведения следует, что. Так как,, тои. Таким образом,.

3. Аналитическая геометрия в пространстве

3.1. Общее уравнение плоскости

Пусть в пространстве задана прямоугольная система координат , точкаи вектор. Выведем уравнение плоскости, проходящей через точкуи перпендикулярной вектору.

Пусть  произвольная точка плоскости . Точкалежит в плоскоститогда и только тогда, когда векторыивзаимно перпендикулярны.

z

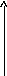
M₀

y

M

O

x

Вектор имеет координаты. Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения, т. е. должно выполняться равенство. Воспользовавшись формулой (2.21), получим:

. (3.1)

Уравнение (3.1)  искомое уравнение плоскости , проходящей через точкуи перпендикулярной вектору, так как ему удовлетворяют координатылюбой точки, лежащей на плоскости, и не удовлетворяют координаты никакой точки, не лежащей на этой плоскости.

Если в уравнении (3.1) раскрыть скобки и обозначить , то получимобщее уравнение плоскости:

. (3.2)

Таким образом, плоскость является поверхностью первого порядка, так как определяется уравнением первой степени.

Теорема 1. Всякое уравнение первой степени вида (3.2) определяет в заданной системе координат плоскость.

Доказательство. Пусть заданы прямоугольная система координат и уравнение, коэффициенты которого удовлетворяют условию, т. е. хотя бы один из коэффициентовотличен от нуля. Для определенности будем считать, что. Уравнение (3.2) имеет решение, так как при фиксированныхииз уравнения (3.2) получим. Следовательно, существует хотя бы одна точка, координаты которой удовлетворяют уравнению (3.2), т. е.. Вычитая это числовое равенство из уравнения (3.2), получим уравнение, эквивалентное данному, поэтому уравнениеопределяет плоскость, проходящую через точкуи перпендикулярную вектору. Теорема доказана.

П р и м е р 30. Составить общее уравнение плоскости, проходящей через точку перпендикулярно вектору.

Решение. С использованием (3.1) имеем: , или.

Определение. Вектор , перпендикулярный плоскости, задаваемой уравнением, называетсянормальным вектором этой плоскости.

Теорема 2. Если два уравнения иопределяют одну и ту же плоскость, то найдется такое число, что справедливы равенства,,,, т.е. коэффициенты уравнений пропорциональны.

Доказательство. Уравнения иопределяют одну и ту же плоскость, поэтому векторыиколлинеарны. Согласно условию (2.28) коллинеарности имеем:, т. е.,,. Подставим выражения для коэффициентовв первое уравнение плоскости, получим:. Выражение, стоящее в скобках, равно, поэтому. Теорема доказана.

3.2. Угол между плоскостями

Рассмотрим две плоскости и, которые задаются уравнениямии.

При любом расположении плоскостей в пространстве один из углов между ними равен углу между их нормальными векторамиии вычисляется по формуле:

. (3.3)

Второй угол между плоскостями равени.

Две плоскости ипараллельны тогда и только тогда, когда их нормальные векторыиколлинеарны. В этом случае

. (3.4)

Условие (3.4) является условием параллельности двух плоскостей, задаваемых уравнениями и.

Две плоскости ивзаимно перпендикулярны тогда и только тогда, когда их нормальные векторыиортогональны, т. е. косинус угламежду ними равен нулю. Поэтому условие перпендикулярности плоскостей определяется соотношением

. (3.5)