
- •3. Аналитическая геометрия в пространстве
- •3.1. Общее уравнение плоскости
- •3.2. Угол между плоскостями
- •3.3. Неполные уравнения плоскости. Уравнение плоскости в отрезках
- •3.4. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой
- •3.5. Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •3.6. Пучки и связки плоскостей
- •3.7. Уравнения прямой в пространстве
3.3. Неполные уравнения плоскости. Уравнение плоскости в отрезках
Определение.
Общее уравнение (3.2) плоскости называется
полным, если
все его коэффициенты
![]() отличны от нуля. Если хотя бы один из
указанных коэффициентов равен нулю, то
уравнение называетсянеполным.
отличны от нуля. Если хотя бы один из
указанных коэффициентов равен нулю, то
уравнение называетсянеполным.
Рассмотрим все возможные виды неполных уравнений.
 .
Уравнение
.
Уравнение
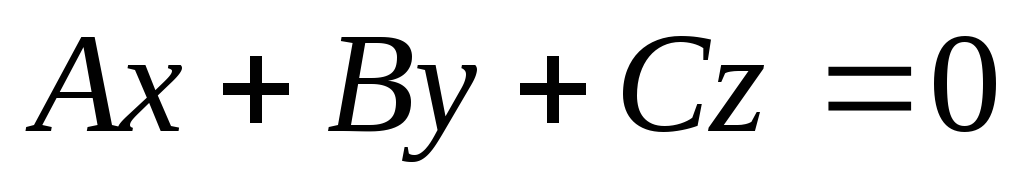 определяет плоскость, проходящую через
начало координат, так как координаты
точки
определяет плоскость, проходящую через
начало координат, так как координаты
точки удовлетворяют этому уравнению.
удовлетворяют этому уравнению. .
Уравнение
.
Уравнение
 определяет плоскость, параллельную
оси
определяет плоскость, параллельную
оси ,
так как нормальный вектор
,
так как нормальный вектор этой плоскости перпендикулярен оси
этой плоскости перпендикулярен оси .
. .
Уравнение
.
Уравнение
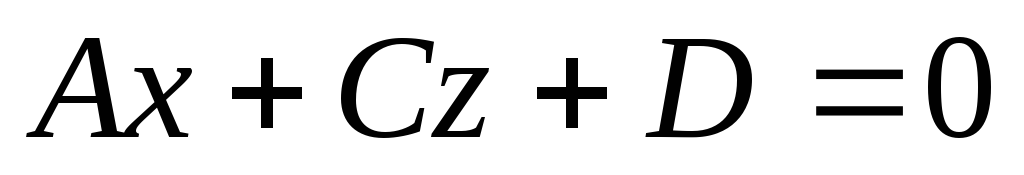 определяет плоскость, параллельную
оси
определяет плоскость, параллельную
оси ,
так как нормальный вектор
,
так как нормальный вектор этой плоскости перпендикулярен оси
этой плоскости перпендикулярен оси .
. .
Уравнение
.
Уравнение
 определяет плоскость, параллельную
оси
определяет плоскость, параллельную
оси ,
так как нормальный вектор
,
так как нормальный вектор этой плоскости перпендикулярен оси
этой плоскости перпендикулярен оси .
. .
Уравнение
.
Уравнение
 определяет плоскость, параллельную
координатной плоскости
определяет плоскость, параллельную
координатной плоскости ,
так как эта плоскость параллельна осям
,
так как эта плоскость параллельна осям и
и .
. .
Уравнение
.
Уравнение
 определяет плоскость, параллельную
координатной плоскости
определяет плоскость, параллельную
координатной плоскости ,
так как эта плоскость параллельна осям
,
так как эта плоскость параллельна осям и
и .
. .
Уравнение
.
Уравнение
 определяет плоскость, параллельную
координатной плоскости
определяет плоскость, параллельную
координатной плоскости ,
так как эта плоскость параллельна осям
,
так как эта плоскость параллельна осям и
и .
. .
Уравнение
.
Уравнение
 определяет координатную плоскость
определяет координатную плоскость ,
так как эта плоскость параллельна
,
так как эта плоскость параллельна и проходит через начало координат.
и проходит через начало координат. .
Уравнение
.
Уравнение
 определяет координатную плоскость
определяет координатную плоскость ,
так как эта плоскость параллельна
,
так как эта плоскость параллельна и проходит через начало координат.
и проходит через начало координат. .
Уравнение
.
Уравнение
 определяет координатную плоскость
определяет координатную плоскость ,
так как эта плоскость параллельна
,
так как эта плоскость параллельна и проходит через начало координат.
и проходит через начало координат.
Рассмотрим
полное уравнение (3.2) плоскости. В этом
уравнении все коэффициенты отличны от
нуля, поэтому его можно переписать в
виде
 ,
или
,
или
![]() ,
(3.6)
,
(3.6)
где
![]() ,
,![]() ,
,![]()
величины отрезков, отсекаемых плоскостью
на осях
величины отрезков, отсекаемых плоскостью
на осях
![]() ,
,![]() и
и![]() соответственно. Уравнение (3.6) называется
уравнением плоскости в отрезках.
соответственно. Уравнение (3.6) называется
уравнением плоскости в отрезках.
3.4. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой
Пусть
три точки
![]() ,
,![]() и
и![]() не лежат на одной прямой. В этом случае
векторы
не лежат на одной прямой. В этом случае
векторы![]() и
и![]()
![]() не коллинеарны, поэтому точка
не коллинеарны, поэтому точка![]() лежит в одной плоскости с точками
лежит в одной плоскости с точками![]() ,
,![]() и
и![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы![]() ,
,![]() и
и![]() компланарны, т. е. тогда и только тогда,
когда смешанное произведение этих трех
векторов равно нулю. Используя выражение
(2.34) смешанного произведения векторов
в координатах, получим необходимое и
достаточное условие принадлежности
точки
компланарны, т. е. тогда и только тогда,
когда смешанное произведение этих трех
векторов равно нулю. Используя выражение
(2.34) смешанного произведения векторов
в координатах, получим необходимое и
достаточное условие принадлежности
точки![]() к плоскости, проходящей через точки
к плоскости, проходящей через точки![]() ,
,![]() и
и![]() :
:
 .
(3.7)
.
(3.7)
Уравнение
(3.7) первой степени и является уравнением
искомой плоскости, проходящей через
три точки
![]() ,
,![]() и
и![]() ,
не лежащие на одной прямой.
,
не лежащие на одной прямой.
3.5. Нормальное уравнение плоскости. Расстояние от точки до плоскости
Рассмотрим
произвольную плоскость
![]() .
Проведем через начало координат
.
Проведем через начало координат![]() прямую
прямую![]() ,
перпендикулярную плоскости
,
перпендикулярную плоскости![]() ,
которую будем называтьнормалью.
Точка
,
которую будем называтьнормалью.
Точка
![]()
пересечение плоскости и нормали. Введем
направление от точки
пересечение плоскости и нормали. Введем
направление от точки
![]() к точке
к точке![]() ,
т. е. на прямой
,
т. е. на прямой![]() возьмем единичный вектор
возьмем единичный вектор![]() ,
направление которого совпадает с
направлением отрезка
,
направление которого совпадает с
направлением отрезка![]() .
Если точки
.
Если точки![]() и
и![]() ,
совпадают, то направление вектора
,
совпадают, то направление вектора![]() выберем произвольно.
выберем произвольно.
z



M

P
y![]()


O


![]()
x
Пусть
![]() ,
,![]()
углы, которые вектор
углы, которые вектор
![]() составляет с осями
составляет с осями![]() ,
,![]() и
и![]() соответственно. Тогда координатами
вектора
соответственно. Тогда координатами
вектора![]() будут направляющие косинусы
будут направляющие косинусы![]() .
Если
.
Если![]()
произвольная точка плоскости
произвольная точка плоскости
![]() ,
проекция вектора
,
проекция вектора![]() на нормаль
на нормаль![]() равна
равна![]() ,
т. е.:
,
т. е.:
![]() .
(3.7)
.
(3.7)
Учитывая,
что
![]() ,
,![]() ,
получим:
,
получим:
![]() .
(3.8)
.
(3.8)
Из соотношений (3.7) и (3.8) следует нормальное уравнение плоскости:
![]() .
(3.9)
.
(3.9)
Теорема 3.
Если точка
![]() имеет координаты
имеет координаты![]() и плоскость
и плоскость![]() задана нормальным уравнением
задана нормальным уравнением![]() ,
то расстояние
,
то расстояние![]() от точки
от точки
![]() до плоскости
до плоскости![]() определяется по формуле
определяется по формуле
![]() .
(3.10)
.
(3.10)
Доказательство.
Пусть
![]()
проекция точки
проекция точки
![]() на направленную нормаль. Тогда в силу
основного алгебраического тождества
на направленную нормаль. Тогда в силу
основного алгебраического тождества![]() или
или![]() ,
откуда следует, что
,
откуда следует, что![]() .
Но
.
Но![]() ,
,![]() ,
т. е.
,
т. е.![]() .
Вектор
.
Вектор![]() имеет координаты
имеет координаты![]() и
и![]() .
Поэтому
.
Поэтому![]()
![]() .
Теорема доказана.
.
Теорема доказана.
Пусть
уравнения
![]() и
и![]() являются общим и нормальным уравнениями
одной и той же плоскости
являются общим и нормальным уравнениями
одной и той же плоскости![]() .
По теореме 2 коэффициенты в этих уравнениях
пропорциональны, т. е.
.
По теореме 2 коэффициенты в этих уравнениях
пропорциональны, т. е.![]() ,
,![]() ,
,![]() .
Так как
.
Так как![]()
![]() ,
то
,
то![]() или
или![]() .
.
Определение.
Число
![]() ,
с помощью которого общее уравнение
плоскости преобразуется к нормальному,
называетсянормирующим множителем.
,
с помощью которого общее уравнение
плоскости преобразуется к нормальному,
называетсянормирующим множителем.
Знак
числа
![]() определяется из условия
определяется из условия![]() ,
т. е. оно имеет знак, противоположный
знаку свободного члена общего уравнения.
Если в уравнении (3.2)
,
т. е. оно имеет знак, противоположный
знаку свободного члена общего уравнения.
Если в уравнении (3.2)![]() ,
то знак нормирующего множителя выбирается
произвольно.
,
то знак нормирующего множителя выбирается
произвольно.
П р и м е р 31.Найти расстояние
![]() от точки
от точки![]() до плоскости
до плоскости![]() .
.
Решение.
Прежде всего нужно общее уравнение
плоскости привести к нормальному виду.
Найдем нормирующий множитель
![]()
![]() .
В общем уравнении плоскости
.
В общем уравнении плоскости![]() ,
поэтому
,
поэтому![]() ,
т. е.
,
т. е.![]() .
Следовательно, нормальное уравнение
плоскости имеет вид
.
Следовательно, нормальное уравнение
плоскости имеет вид![]() .
Тогда
.
Тогда![]() .
.
Следствие.
Если точка
![]() имеет координаты
имеет координаты![]() и плоскость
и плоскость![]() задана общим уравнением
задана общим уравнением![]() ,
то расстояние
,
то расстояние![]() от точки
от точки
![]() до плоскости
до плоскости![]() определяется по формуле
определяется по формуле
![]() .
(3.11)
.
(3.11)
Доказательство.
Направляющие косинусы нормали плоскости
связаны с коэффициентами общего уравнения
плоскости соотношениями
![]() ,
,![]() ,
,![]() ,
где
,
где![]()
нормирующий множитель. Учитывая, что
нормирующий множитель. Учитывая, что
![]() ,
преобразуем формулу (3.10):
,
преобразуем формулу (3.10):![]()
![]() =
=![]() =
=![]()
![]() .
Следствие доказано.
.
Следствие доказано.
