
П р и м е р 23.
Даны векторы
![]() ,
,![]() ,
,![]() .
Найти разложение вектора
.
Найти разложение вектора![]() по базису
по базису![]() ,
,![]() ,
,![]() .
.
Решение.
Для разложение вектора
![]() по базису
по базису![]() ,
,![]() ,
,![]() необходимо найти такие числа
необходимо найти такие числа![]() ,
,![]() и
и![]() ,
чтобы выполнялось равенство
,
чтобы выполнялось равенство![]() .
Если два вектора равны, то равны и их
соответствующие координаты, поэтому
относительно
.
Если два вектора равны, то равны и их
соответствующие координаты, поэтому
относительно![]() ,
,![]() и
и![]() имеем систему уравнений
имеем систему уравнений Векторы
Векторы![]() ,
,![]() ,
,![]() по условию задачи образуют базис, поэтому
главный определитель системы отличен
от нуля и по теореме Крамера она имеет
единственное решение:
по условию задачи образуют базис, поэтому
главный определитель системы отличен
от нуля и по теореме Крамера она имеет
единственное решение:![]() ,
,![]() ,
,![]() .
Таким образом,
.
Таким образом,![]() .
.
2.5. Скалярное произведение векторов
Определение.
Скалярным произведениемдвух
ненулевых векторов
![]() и
и
![]() называется число (скаляр), равное
произведению длин этих векторов на
косинус угла между ними, т. е.
называется число (скаляр), равное
произведению длин этих векторов на
косинус угла между ними, т. е.
![]() ,
(2.16)
,
(2.16)
где
![]()
угол между векторами
угол между векторами
![]() и
и
![]() .
.
Если
хотя бы один из векторов
![]() или
или
![]()
нулевой, то угол между векторами не
определен, и скалярное произведение
полагается равным нулю.
нулевой, то угол между векторами не
определен, и скалярное произведение
полагается равным нулю.
Проекцию
вектора
![]() на ось, определяемую вектором
на ось, определяемую вектором
![]() ,
обозначим
,
обозначим
![]() .
По определению проекции вектора на ось
имеем:
.
По определению проекции вектора на ось
имеем:![]() .
Тогда скалярное произведение двух
ненулевых векторов
.
Тогда скалярное произведение двух
ненулевых векторов
![]() и
и
![]() определяется формулой
определяется формулой
![]() .
(2.17)
.
(2.17)
Учитывая,
что в определении скалярного произведения
векторы
![]() и
и
![]() взаимозаменяемые, его можно представить
в виде
взаимозаменяемые, его можно представить
в виде
![]() .
(2.18)
.
(2.18)
Соотношения (2.17) и (2.18) позволяют сформулировать другое определение скалярного произведения.
Определение.
Скалярным произведениемдвух
ненулевых векторов
![]() и
и
![]() называется число (скаляр), равное
произведению длины одного из этих
векторов на проекцию другого вектора
на ось, определяемую первым из указанных
векторов.
называется число (скаляр), равное
произведению длины одного из этих
векторов на проекцию другого вектора
на ось, определяемую первым из указанных
векторов.
Физический
смысл скалярного произведения заключается
в следующем: если точка приложения силы,
задаваемой постоянным вектором
![]() ,
перемещается вдоль вектора
,
перемещается вдоль вектора
![]() ,
то работа этой силы определяется
равенством
,
то работа этой силы определяется
равенством
![]() ,
где
,
где![]()
угол между векторами
угол между векторами
![]() и
и
![]() ,
т. е. работа равна скалярному произведению
векторов
,
т. е. работа равна скалярному произведению
векторов
![]() и
и
![]() .
.
Теорема 8. Необходимым и достаточным условием ортогональности (перпендикулярности) двух векторов является равенство нулю их скалярного произведения.
Доказательство.
Необходимость. Пусть
векторы
![]() и
и
![]() ортогональны,
ортогональны,![]()
угол между ними, тогда
угол между ними, тогда
![]() ,
и в силу формулы (2.16)
,
и в силу формулы (2.16)![]() .
.
Достаточность.
Пусть
![]() .
Докажем, что векторы
.
Докажем, что векторы
![]() и
и
![]() ортогональны. Если хотя бы один из
векторов равен нулевому вектору, то он
имеет неопределенное направление, и
можно считать, что векторы ортогональны.
Если оба вектора
ортогональны. Если хотя бы один из
векторов равен нулевому вектору, то он
имеет неопределенное направление, и
можно считать, что векторы ортогональны.
Если оба вектора
![]() и
и
![]() ненулевые, то
ненулевые, то![]() ,
,![]() ,
поэтому из (2.16) следует, что
,
поэтому из (2.16) следует, что![]() ,
т, е. векторы
,
т, е. векторы
![]() и
и
![]() ортогональны. Теорема доказана.
ортогональны. Теорема доказана.
Если
два вектора привести к общему началу,
то в качестве угла
![]() между этими векторами можно взять любой
из углов
между этими векторами можно взять любой
из углов![]() или
или![]() .
.
![]()
![]()

![]()
![]()



Действительно,
сумма углов
![]() и
и![]() равна
равна![]() ,
поэтому
,
поэтому![]() .
В определение скалярного произведения
входит сомножителем только косинус
угла между векторами. Из двух углов
.
В определение скалярного произведения
входит сомножителем только косинус
угла между векторами. Из двух углов![]() и
и![]() между векторами один всегда не более
между векторами один всегда не более![]() .
За угол
.
За угол![]() между векторами принимается наименьший
из углов
между векторами принимается наименьший
из углов![]() и
и![]() ,
т. е.
,
т. е.![]() .
.
Если
скалярное произведение двух ненулевых
неколлинеарных векторов
![]() и
и
![]() положительно (отрицательно), то эти два
вектора составляют острый (тупой) угол.
положительно (отрицательно), то эти два
вектора составляют острый (тупой) угол.
Свойства скалярного произведения:
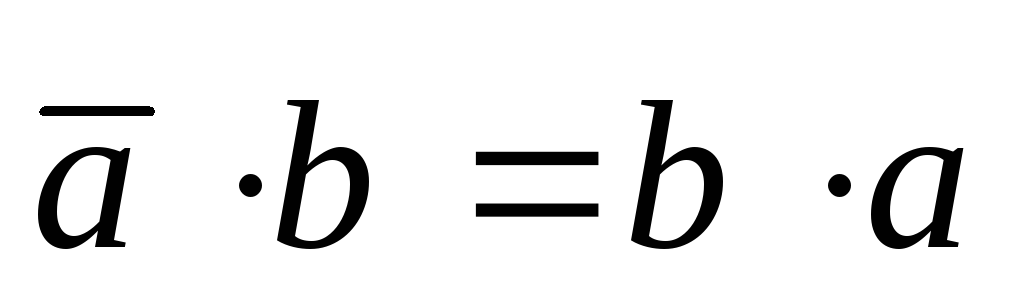 .
.
Доказательство.
Это свойство непосредственно вытекает
из определения скалярного произведения:
![]() .
Свойство доказано.
.
Свойство доказано.
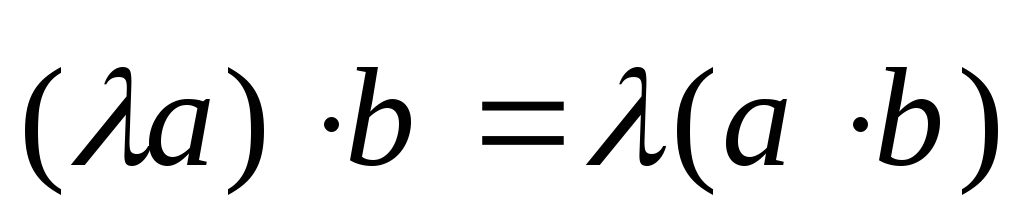 .
.
Доказательство.
Для доказательства этого свойства
воспользуемся формулой (2.18) для определения
скалярного произведения и свойствами
проекций векторов на ось:
![]() .
Свойство доказано.
.
Свойство доказано.
 .
.
Доказательство.
Воспользуемся
формулой (2.18) для определения скалярного
произведения и свойствами проекций
векторов на ось. Получим:
![]() .
Свойство доказано.
.
Свойство доказано.
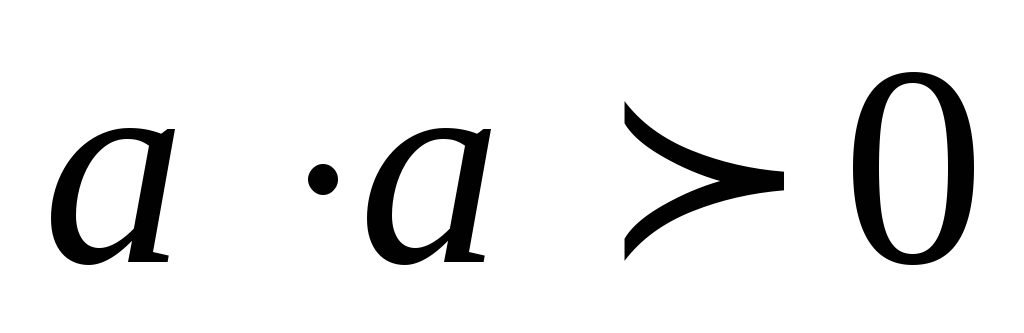 ,
если
,
если
 ,
и
,
и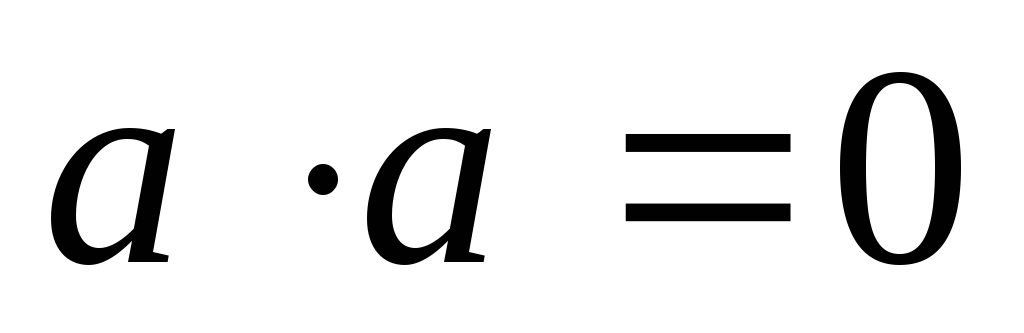 ,
если
,
если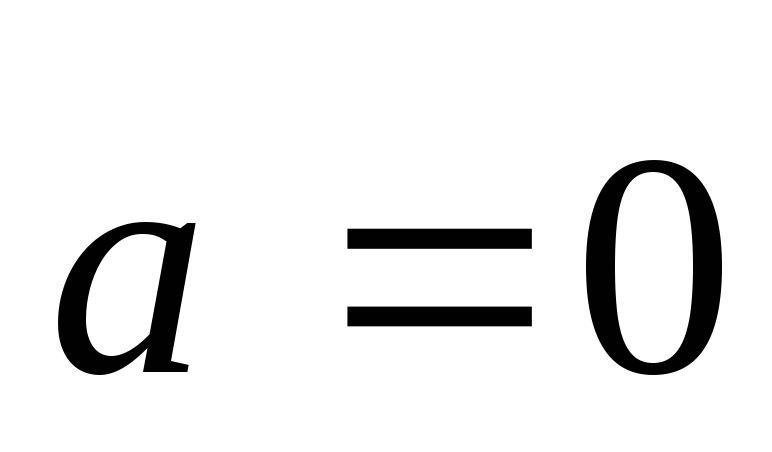 .
.
Доказательство.
Из определения скалярного произведения
с использованием соотношения (2.16)
следует, что
![]() .
Если
.
Если![]() ,
то
,
то![]() и
и![]() .
Если же
.
Если же![]() ,
то
,
то![]() ,
поэтому
,
поэтому![]() .
Свойство доказано.
.
Свойство доказано.
Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, не учитывая порядок векторных сомножителей и сочетая числовые множители.
Из
определения и свойств скалярного
произведения векторов следует, что для
базисных векторов
![]() ,
,![]() ,
,![]() выполняются соотношения
выполняются соотношения
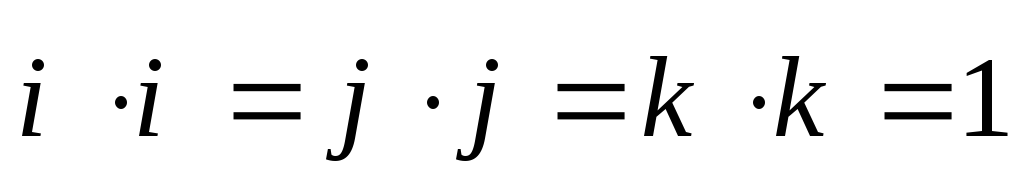 ;
(2.19)
;
(2.19)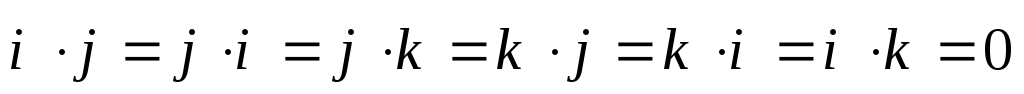 .
(2.20)
.
(2.20)
Теорема 9.
Если векторы
![]() и
и![]() заданы своими координатами, т. е.
заданы своими координатами, т. е.![]() ,
,![]() ,
то скалярное произведение векторов
,
то скалярное произведение векторов![]() и
и![]() вычисляется по формуле
вычисляется по формуле
![]() .
(2.21)
.
(2.21)
Доказательство.
Разложим векторы
![]() и
и![]() по базису
по базису![]() ,
,![]() ,
,![]() ,
получим
,
получим![]() ,
,![]() .
Тогда по свойствам скалярного произведения
векторов, используя формулы (2.19), (2.20),
имеем
.
Тогда по свойствам скалярного произведения
векторов, используя формулы (2.19), (2.20),
имеем![]()
![]()
![]() .
Теорема доказана.
.
Теорема доказана.
Следствие.
Угол
![]() между ненулевыми векторами
между ненулевыми векторами![]() и
и![]() определяется по формуле
определяется по формуле
![]() .
(2.22)
.
(2.22)
Доказательство.
По определению
скалярного произведения двух ненулевых
векторов
![]() ,
поэтому
,
поэтому![]() .
Воспользовавшись формулами (2.21) и (2.9)
для скалярного произведения и длин
векторов, заданных своими координатами,
получим формулу (2.22).
.
Воспользовавшись формулами (2.21) и (2.9)
для скалярного произведения и длин
векторов, заданных своими координатами,
получим формулу (2.22).
Замечание.
Если один из векторов
![]() или
или![]() является нулевым, то угол между векторами
определяется неоднозначно и может быть
выбран произвольным.
является нулевым, то угол между векторами
определяется неоднозначно и может быть
выбран произвольным.
П р и м е р 24.
Дано, что
![]() ,
,![]() .
Определить, при каком значении
.
Определить, при каком значении![]() векторы
векторы![]() и
и![]() будут взаимно перпендикулярны.
будут взаимно перпендикулярны.
Решение.
Условием перпендикулярности векторов
является равенство нулю их скалярного
произведения, т. е.
![]() .
По свойствам скалярного произведения
.
По свойствам скалярного произведения![]()
![]() .
Таким образом,
.
Таким образом,![]() ,
или
,
или![]() .
.
П р и м е р 25.
Векторы
![]() и
и![]() образуют угол
образуют угол![]() .
Зная, что
.
Зная, что![]() ,
,![]() ,
вычислить угол
,
вычислить угол![]() между векторами
между векторами![]() и
и![]() .
.
Решение.
Для нахождения косинуса угла
![]() между векторами
между векторами![]() и
и![]() воспользуемся соотношением (2.22). По
формуле (2.21):
воспользуемся соотношением (2.22). По
формуле (2.21):![]() .
Найдем длины векторов
.
Найдем длины векторов![]() и
и![]() ,
используя свойства скалярного
произведения:
,
используя свойства скалярного
произведения:![]()
![]() .
Аналогично находим, что
.
Аналогично находим, что![]() .
Тогда
.
Тогда![]() и
и![]() .
.
