Если уравнение плоскости является неполным (или), то, рассуждая аналогичным образом, получим уравнение (1.15), в котором соответственноили.

1.8. Преобразование прямоугольных координат

Пусть дана точка на плоскости. Перенесем начало прямоугольной системы координат в точку, где координаты нового начала в старой системе координат .

M

M_y

x

M_x

O

Тогда ,, или

, . (1.16)

Выражение (1.16) называется формулой преобразования координат при параллельном переносе осей.

Рассмотрим прямоугольную систему координат , полученную из поворотом на угол.

y

M

M_y



x

M_x

O

Из треугольников иимеем:,. Из треугольникови

,

, т. е.

, . (1.17)

Формулы (1.17) показывают преобразование прямоугольных координат при повороте осей. Из (1.17) следует, что ,.

С учетом (1.16) и (1.17) можно записать преобразование прямоугольных координат при повороте и параллельном переносе осей:

, . (1.18)

1.9. Полярная система координат

Выберем на плоскости некоторую точку О (полюс) и некоторый выходящий из нее луч Ох и укажем единицу масштаба.

М

у

у



х



х

О

Определение. Полярными координатами точки М называются два числа  и , первое из которых (полярный радиус ) равно расстоянию точки М от полюса О, а второе (полярный угол )  угол, на который надо повернуть против часовой стрелки луч Ох до совмещения с лучом ОМ.

При этом предполагается, что точка М не совпадает с полюсом. Для полюса О полярный радиус  равен нулю, а полярный угол  не определен, т. е. ему можно присвоить любое значение.

Точку плоскости М с полярными координатами  и  обозначают символом М (, ).

Для того чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат (, ) было взаимно однозначным, обычно считают, что 0     , 0    . Однако в некоторых случаях приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по часовой стрелке.

Установим связь между полярными и прямоугольными координатами одной и той же точки плоскости. Будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью.

Пусть точка М имеет полярные координаты  и  и прямоугольные координаты х и у. Тогда

. (1.19)

Формулы (1.19) выражают прямоугольные координаты через полярные. Выражения полярных координат точки через прямоугольные следуют из формул (1.19):

. (1.20)

Вторая из этих формул определяет два значения полярного угла, так как  изменяется от 0 до . Из этих двух значений выбирается то, при котором удовлетворяются равенства (1.19), т. е. нужно, используя знаки х и у, определить квадрант, в котором находится точка М. Когда х = 0, tg  не может быть вычислен по формулам (1.20). В этом случае (еслиу  0) и (еслиу  0).

Для простоты нахождения полярного угла  через прямоугольные координаты можно воспользоваться следующей таблицей:

Значение х	Значение у	Значение 
х = 0	у  0
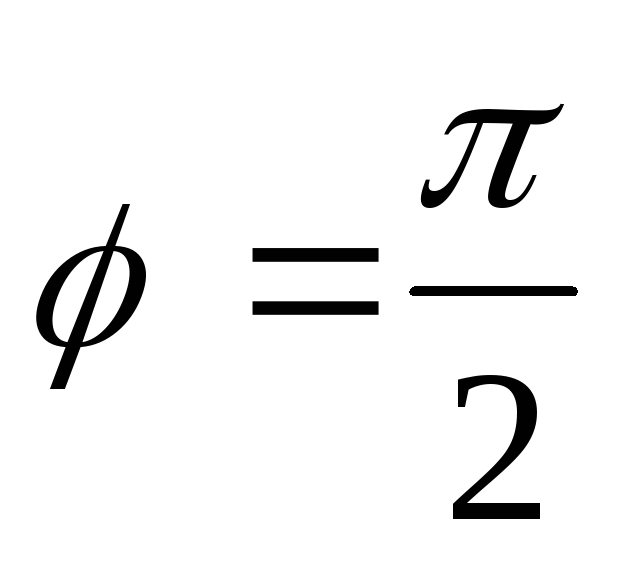
х = 0	у  0
х  0	у  0
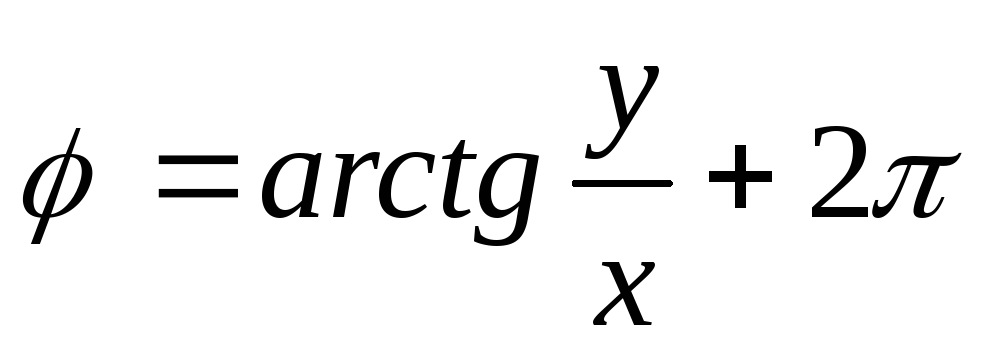
х  0	у = 0
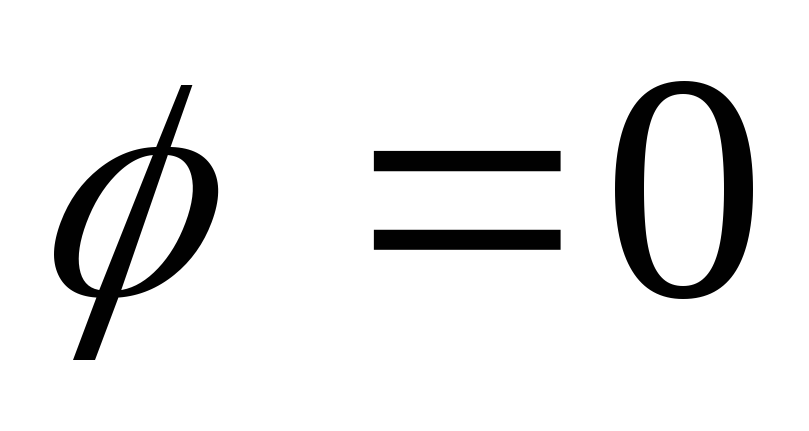
х  0	у  0
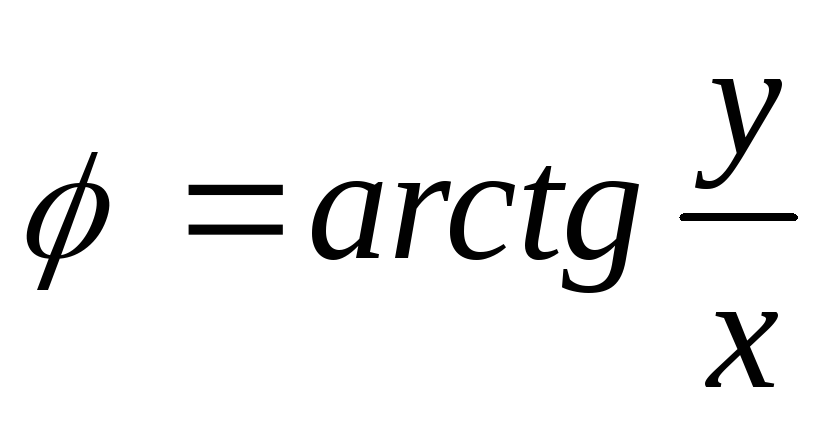
х  0	у  0
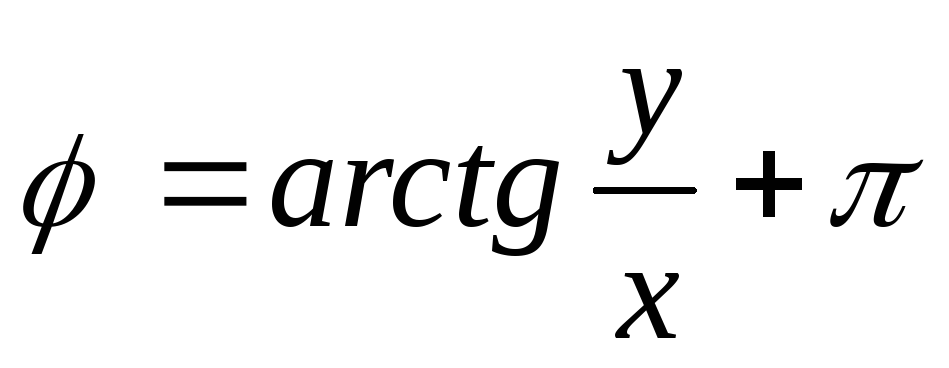
х  0	у = 0
х  0	у  0