
ответы / 15,18,19,20 Математическая модель механики твердо деформируемого тела
.docxМатематическая модель механики твердо деформируемого тела
Полная математическая модель механики твердо деформированного тела состоит из трех частей: уравнения равновесия, геометрические соотношения и физические соотношения. Рассмотрим каждую из частей более подробно.
I. Уравнения равновесия.
В твердо деформированном теле выберем некоторую точку А с координатами (x,y,z). Вблизи этой точки вырежем объем dV = dxdydz. На каждой грани вырезанного элемента действует по три напряжения: одно нормальное и два касательных (рис. 29). Кроме этого на элементарный объем действуют массовые силы R(X, Y, Z).

Рис. 29
Так как все тело находится в равновесии, то в равновесии находится и элементарный объем и, следовательно, можно составить три уравнения равновесия сил в проекциях на оси координат. Напомним, что для того чтобы получить силу, необходимо умножить напряжение на площадь грани, на которой оно действует.
-xdydz + (x + dxx)dydz - yxdxdz + (yx + dyyx)dxdz –
- zxdxdy + (zx + dzzx)dxdy + Xdxdydz = 0,
раскроем скобки и распишем частные производные
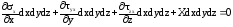 ,
,
поделим уравнение на элементарный объем
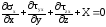 .
(54)
.
(54)
Аналогично запишем уравнения равновесия по двум другим осям координат:
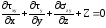
 .
(55)
.
(55)
Полученная система уравнений содержит шесть неизвестных компонентов: три нормальных напряжения и три касательных напряжения (с учетом закона парности касательных напряжений). Следовательно, этих уравнений недостаточно для решения поставленной задачи.
II. Геометрические соотношения.
В теле выберем некоторую точку А с координатами (x,y,z). После нагружения и деформации (рис.30) точка А переместилась в точку А1 с координатами (х1, у1, z1) на малую величину r (х, у, z).
Введем обозначения
х = х1 – х = U,
у = у1 – у = V, (56)
z = z1 – z = W,
где U, V, W – перемещения вдоль координатных осей Х, У, Z.
Теперь возьмем отрезок АВ бесконечно малой длины dS с направляющими косинусами (l, m, n). Изменение длины отрезка под нагрузкой dS1 - dS = dS называется абсолютным удлинением или приращением.



Рис. 30
Отношение приращения к первоначальной длине отрезка называется относительным удлинением или линейной деформацией:
=
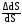 .
(57)
.
(57)
Пусть отрезок dS имеет проекции по координатным осям (dx, dy, dz). Зная направляющие косинусы отрезка, найдем величину проекций:
dx=ldS,
dy=mdS, (58)
dz=ndS.
Найдем длину отрезка dS через проекции:
dS2 = dx2 + dy2 + dz2.
Продифференцируем это выражение:
2dSdS = 2dxdx + 2dydy + 2dzdz. (59)
учитывая выражения (56), можно записать:
dx = dx =dU,
dy = dy = dV, (60)
dz = dz = dW.
Подставим полученные выражения в (59):
dSdS = dxdU + dydV + dzdW,
следовательно, приращение отрезка равно:
dS =
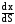 dU
+
dU
+
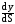 dV
+
dV
+
 dW
= ldU
+ mdV
+ ndW.
(61)
dW
= ldU
+ mdV
+ ndW.
(61)
найдем линейную деформацию по формуле (57) с учетом выражения (61):
=
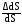 =
=
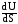 l
+
l
+
 m
+
m
+
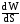 n.
(62)
n.
(62)
Перемещения U, V, W являются функциями трех координат, так как они зависят от положения точки в теле по отношению к опорам и приложенным нагрузкам. Следовательно, полный дифференциал является суммой частных производных.
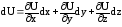 ,
,
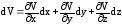 ,
(63)
,
(63)
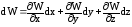 .
.
Поделим каждое из уравнений (63) на dS:
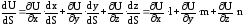 ,
,
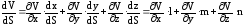 ,
(64)
,
(64)
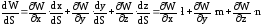 .
.
Подставим полученные выражения (64) в уравнение деформации (62):
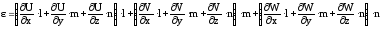
Раскрыв скобки и сгруппировав слагаемые по направляющим косинусам, получим полное выражение для линейной деформации:
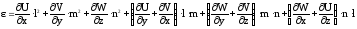
Введем обозначения
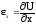 ,
,
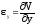 ,
,
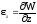 ,
(65)
,
(65)
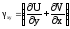 ,
,
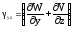 ,
,
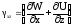 .
.
Эти выражения получили название формул Коши. Они связывают между собой компоненты тензора деформаций и перемещения точки. С учетом формул Коши деформация в произвольном направлении получит следующий вид:
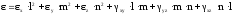 .
(66)
.
(66)
Определим физический смысл введенных обозначений. Формула (66) справедлива для любого направления, поэтому возьмем отрезок dS параллельно оси Х, тогда его длина определяется проекцией на эту ось dS=dx и направляющие косинусы равны l=1, m=n=0. Согласно уравнению (66) деформация отрезка в этом случае будет равна:
=
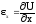 .
.
т. о. х – линейная деформация в направлении оси Х; аналогично у – линейная деформация в направлении оси Y; z – линейная деформация в направлении оси Z.
Теперь определим, что такое . Возьмем в теле прямой угол АВС со сторонами, параллельными осям координат. После нагружения тела, угол деформировался и занял положение А1В1С1 (рис. 31).

Рис. 31
Точка А переместилась вдоль оси Y на V, а точка В вдоль той же оси переместилась на V+dxV. При этом длина отрезка dx стала dx+dx. Рассмотрим треугольник А1В1В’:
tg
=
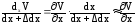 .
(67)
.
(67)
Аналогично рассмотрим треугольник А1С1С’:
tg
=
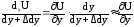 .
(68)
.
(68)
Первоначально прямой угол уменьшился на +. С учетом того, что при малых углах tg получаем:
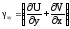 .
.
Таким образом, получается, что ху – изменение прямого угла со сторонами, параллельными координатным осям, т. е. угловая деформация в плоскости ХY. Аналогично можно получить две других угловых деформации.
III. Физические соотношения.
При испытаниях на растяжение был экспериментально установлен закон Гука:
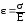 .
(69)
.
(69)
Также опытным путем установлены модуль Юнга Е – коэффициент пропорциональности между нормальным напряжением и линейной деформацией и коэффициент Пуассона – отношение поперечной деформации к продольной.
Рассмотрим закон Гука в главных осях.


Рис. 32
При одноосном напряженном состоянии (рис.32) деформации по трем осям будут равны:
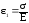 ,
(70)
,
(70)
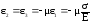 .
.
 При
рассмотрении трехосного напряженного
состояния (рис.33) воспользуемся принципом
суперпозиции, т.е. найдем деформации по
осям от каждого напряжения в отдельности.
При
рассмотрении трехосного напряженного
состояния (рис.33) воспользуемся принципом
суперпозиции, т.е. найдем деформации по
осям от каждого напряжения в отдельности.
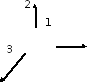
Рис. 33
От напряжения 1:
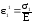 ,
,
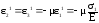 .
.
От напряжения 2:
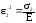 ,
,
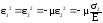 .
.
От напряжения 3:
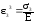 ,
,
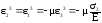 .
.
Найдем суммарные деформации по координатным осям.
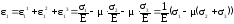 ,
,
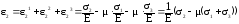 ,
(71)
,
(71)
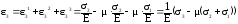 .
.
Формулы (71) представляют собой закон Гука в главных осях. Эти формулы связывают главные напряжения и главные деформации. Вне главных осей существуют касательные напряжения и искажение углов. Следовательно, существует связь между ними. Для установления этой связи перейдем от главных осей к произвольным:
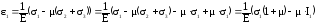 .
(72)
.
(72)
Нормальное напряжение 1 можно выразить по основной квадратичной форме (33) через напряжения в произвольных осях:
1 = xl2 + ym2 +zn2 + 2yxml + 2zxnl + 2zynm.
Подставим это выражение в формулу (72) и умножим первый инвариант на сумму квадратов направляющих косинусов (l2 + m2 + n2 = 1)
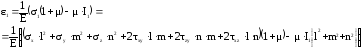
Раскроем скобки и сгруппируем слагаемые по направляющим косинусам:
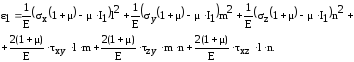
Сравним полученное выражение с квадратичной формой деформации в произвольном направлении (66):
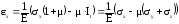 ,
,
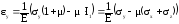 ,
,
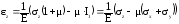 ,
(73)
,
(73)
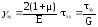 ,
,
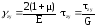 ,
,
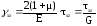 .
.
где G =
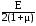 - модуль сдвига, постоянная величина,
являющаяся характеристикой материала.
- модуль сдвига, постоянная величина,
являющаяся характеристикой материала.
Уравнения (73) являются обобщенным законом Гука, выражающим связь между напряжениями и деформациями.
Таким образом, рассмотрев три части математической модели, мы имеем 15 уравнений (3 уравнения равновесия, 6 формул Коши, 6 уравнений обобщенного закона Гука) и 15 неизвестных (3 перемещения по координатным осям, 3 нормальных напряжения, 3 касательных напряжения, 3 линейных деформации, 3 угловых деформации).
Построение математической модели механики твердо деформированного тела – предмет изучения линейной теории упругости. Полученная математическая модель не является ещё полной, так как часть уравнений (формулы Коши и уравнения равновесия) имеют дифференциальный вид. Их нужно интегрировать. В результате чего появляются постоянные интегрирования, то есть дополнительные неизвестные. В обыкновенных дифференциальных уравнениях это константы, для уравнений в частных производных это функции. Поэтому необходимо существование дополнительных условий. Это так называемые граничные условия – условия на границе данного тела (на поверхности).
Граничные условия бывают трех типов: силовые, геометрические и смешанные
