
эконометрика с косяками
.pdf
1, _ если _ экология благоприятная
Eco (X ) = 0, _ иначе
4
–это – фиктивная переменная
Полулогарифмическая модель:
log(Price) 0 1 log(Dist) 2 log(House)
3 log(Area) 4Eco
НАЙДИТЕ: |
|
|
b _____, P |
_____? |
|
0 |
val |
|
b _____, P |
_____? |
|
1 |
val |
|
b _____, P |
_____? |
|
2 |
val |
|
b _____, P |
_____? |
|
3 |
val |
|
b _____, P |
_____? |
|
4 |
val |
|
Какие из этих коэффициентов значимы?
Radj2 _____?
41

Содержательная интерпретация найденных коэффициентов.
Price = A(Dist)b1 (House)b2 (Area)b3 eb4Eco
( A = eb0 )
(запишите в таком виде полученную Вами модель, подставив найденные коэффициенты )
Вопросы:
1. Пусть имеется два одинаковых дома с участком, но один из них на 100 км, а второй
– на 101км.
Как будут отличаться их цены?
2.Пусть имеется два одинаковых дома с участком, но один из них – с хорошей экологией, а другой – нет.
Как будут отличаться их цены?
Ловушка, связанная с введением дамми-переменных: |
||||||||||
Если у переменной z j |
есть k градаций, то есть риск ввести k дамми-переменных. |
|||||||||
## zi 2.4 |
|
1, |
если i-наблюдение осуществлено зимой, |
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
0, |
иначе. |
|
|
|
|
|
||
месяц |
|
z 2.1 |
|
z 2.2 |
|
z 2.3 |
z 2.4 |
В данной модели присутствует линейная зависимость |
||
январь |
|
0 |
|
0 |
|
|
0 |
1 |
переменных: |
z 2.1 z 2.2 z 2.3 z 2.4 x 0 1 |
февраль |
|
0 |
|
0 |
|
|
0 |
1 |
(полная мультиколлинеарность). |
|
март |
|
1 |
|
0 |
|
|
0 |
0 |
Матрица X T X вырожденная, обратной матрицы X T X 1 |
|
апрель |
|
1 |
|
0 |
|
|
0 |
0 |
||
Май |
|
1 |
|
0 |
|
|
0 |
0 |
не существует, формулы МНК не работают! |
|
июнь |
|
0 |
|
1 |
|
|
0 |
0 |
Число дамми-переменных должно быть на |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
единицу меньше числа градаций соответствующей |
|
|
|
|
|
|
|
|
|
|
42 |
|
|
|
|
|
|
|
|
|
|
категоризованной переменной! |
|
июль |
0 |
1 |
0 |
0 |
август |
0 |
1 |
0 |
0 |
сентябрь |
0 |
0 |
1 |
0 |
октябрь |
0 |
0 |
1 |
0 |
ноябрь |
0 |
0 |
1 |
0 |
декабрь |
0 |
0 |
0 |
1 |
Контрольное задание (файл Чебуреки2.sf)
Менеджер новой чебуречной не уверен в правильности выбранной цены на чебуреки, поэтому в течение 12 недель он варьирует цену и записывает количество проданных чебуреков.
В файле чебуреки2.sf приведены результаты его экспериментов (P-цена, Q- количество).
1.Постройте регрессионную модель для количества проданных чебуреков в зависимости от цены.
2.Найдите, при какой цене выручка от продаж будет максимальной.
(Конец 1 дня)
--------------------------------------------------------------------------------
Logit и Probit модели
Бинарные результирующие показатели и связанные с ними логит- и пробит-модели
x 1 , x 2 ,..., x p |
|
0 |
y |
||
|
|
1 |
0, нет ## Возраст, образование, стаж, желаемый уровень зарплаты безработный
1, да
43

Если построить |
линейную регрессионную |
зависимость |
|
y |
0 |
x 1 ... |
p |
x p , |
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
непонятна интерпретация значений |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
yˆi Xi , измеренных в непрерывной количественной |
||||||||||||||
шкале. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Выход: построить регрессионную зависимость вероятности |
P y 1 |
от |
X |
! |
|
|||||||||
Непосредственная |
зависимость |
P y 1 |
0 |
x 1 ... |
p |
x p |
|
плоха, так |
|
как |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
вероятность выходит за пределы отрезка [0; 1], лучше подобрать функцию F X : |
|
|
||||||||||||
P y 1 F X F z .
Свойства:
1.F z – монотонно возрастает.
2.F z 0; 1 .
3.F z 0 при z .
4.F z 0 при z .
p=F(z) |
|
|
1 |
|
|
0,5 |
|
|
0 |
|
z |
-5 |
0 |
5 |
44
Пример 5 ( файл Titanic.sf)
От чего и как зависела вероятность выжить на Титанике?
В данном примере зависимая переменная
(Y) – это качественная переменная, принимающая два значения, пусть 1 – если пассажир выжил и 0 – в противном случае. Все остальные переменные – зависимые.
(описание переменных можно найти в файле titanic3info.txt ). Для нас важны следующие переменные:
Survived =1 или 0, - выживаемость, Age – возраст,
Fare – стоимость билета, Pclass – класс каюты,
Sibsp – количество братьев/сестер, parch - количество родителей/детей sex – пол,1-ж, 2-м
y = |
1 |
|
|
|
|
|
|
|
|
1+ e- z |
, |
|||
где |
|
|
|
|
z b0 b1x1 ... bk xk .
45

y
1
z
Такая модель называется логистической
(logit).
Данная функция принимает значения из отрезка [0,1] и ее значения можно интерпретировать, как прогнозируемые вероятности появления 1 (в нашем примере – вероятность выжить).
Вместо логистической функции, можно было использовать функцию
|
|
1 |
|
z |
x2 |
1 |
|
||
y |
|
|
e |
|
dx Ф(x) |
|
|||
|
|
2 |
|||||||
|
|
|
|
|
|||||
|
2 , |
||||||||
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
||
где Ф(x) - функция Лапласа.
Это- probit модель. (В нашей версии SGее нет).
46
Построим логистическую модель для нашего примера.
В главном меню StatGraphics выбираем:
Special/Advance Regression/Logistic Regression
Вполе Dependent Value заносим survived ,
вполе Quantitative Factors –age, fare, pclass, sibsp, parch в , в поле Categorical Factors – sex..
Смотрим результаты. Также как и для обычной регрессионной модели нас будет интересовать значимость найденных коэффициентов (см.соотв. Pval) и качество подгонки модели (Adjusted Percentage).
1)Какие коэффициенты незначимы?
2)Последовательно исключите соответствующие переменные.
3)Что осталось?
4)На графиках (Grafical Option/Plot of Fitted Model) – посмотрите, как зависит вероятность выжить от
i.возраста,
ii.от пола,
iii.от класса каюты?
47
Метод главных компонент.
Иногда метод главных компонент называют преобразованием Кархунена-Лоэва (англ. Karhunen-Loeve) или преобразованием Хотеллинга (англ. Hotelling transform).
Геометричская интерпретация. Связь с матрицей ковариаций.
При пошиве костюма портной делает 8 – 10 измерений фигуры человека, но при покупке готовой одежды мы обычно учитываем только два измерения: размер и рост, т.е. какие то измерения не очень существенны.
Пусть имеется n объектов (например – людей), и каждый из объектов характеризуется набором из k признаков (например – биометрических характеристик человека). Эти данные можно представить в виде матрицы:
|
(1) |
x1 |
|
X x2(1) |
|
|
(1) |
xn
x1(2) ...
x2(2) ...
xn(2) ...
x1(k ) x2(k ) xn(k )
Каждая строка в этой матрице – это объект, а каждый столбец – это признак.
48

Пусть k=3, тогда каждый объект будет изображаться точкой в трехмерном пространстве, и мы получим облако из n точек.
Мы попытаемся от исходной системы координат
( X (1) , X (2) , X (3) ) X
перейти к новой системе следующим образом: начало новой системы координат (главных компонент)
(Y (1) , Y (2) , Y (3) ) Y
мы выберем в «центре тяжести» облачка точек (такая точка называется центроидом ).
Направление первой главной компоненты
– оси Y (1) мы выберем так, чтобы
рассеяние точек облачка вдоль этой оси было максимально
(точнее: мы проектируем все точки на ось и направление оси выбираем так, чтобы выборочная дисперсия для проекций была максимальна).
49
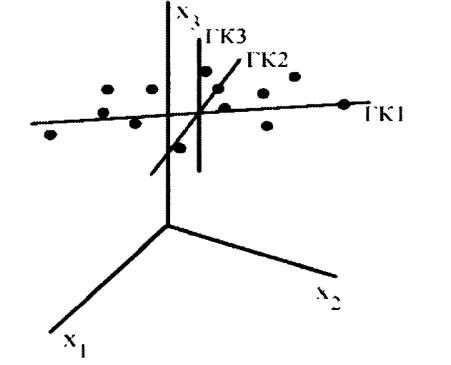
 Первая главная компонента максимизирует выборочную дисперсию проекций данных.
Первая главная компонента максимизирует выборочную дисперсию проекций данных.
Вторая главная компонента должна быть ортогональна предыдущей, поэтому в плоскости ортогональной к построенной оси мы выбираем такое направление, вдоль которого рассеяние точек макимально
(т.е. дисперсия для проекций на эту ось – масимальна) и т.д.
50
