эконометрика с косяками

А.Бююль, П.Цефель SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей ДиаСофт, 2005 г.

Программные средства

1. Statgraphics

Тюрин, Макаров Дюк

2. Statistica

Боровиков, Ивченко Прогнозирование

3. SPSS

Бююуль

SPSS-руководство по применению Эл.библ. социол.ф-та МГУ http://lib.socio.msu.ru

http://www.spsstools.ru/spss.htm

форум истфака МГУ: http://forum.tssi.ru/index.php?showtopic=1207

Programming and Data Management for SPSS 16.0: A Guide for SPSS and SAS® Users

4.STATA Колеников

5.STADIA Кулаичев

6.EVIEWS документация (англ)

==================================================================

1.Сведения из теории вероятностей и статистики

Математическое ожидание и дисперсия, их выборочные оценки.

Коэффициент корреляции и его свойства, теоретический и выборочный к.к.

Теоретическая и выборочная функция регрессии, В каких случаях можно считать, что функция регрессии линейна.

2

Содержательная формулировка ЦПТ

Типичные распределения в статистике

МНК для простой линейной регрессии

Оценка гипотез. Ошибки первого и второго рода. НКО, что такое

P-value в SG

0.1. Элементы теории вероятностей .

Случайные величины и их числовые характеристики

Вероятностью Р(А) события А называется численная мера степени возможности появления этого события.

Согласно классическому определению, вероятность события А равна отношению числа случаев m, благоприятствующих ему, к общему числу случаев n, т.е.

Р(А) = m/n.

При определенных условиях в качестве оценки вероятности события Р(А) может быть использована статистическая вероятность Р*(А), т.е. относительная частота (частость) W(A) появления события А в n произведенных испытаниях.

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее не известно).

Более строго случайная величина X определяется как функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), областью изменения которой является числовая прямая R, т.е.

X : R,

3

где — элементарный исход (или элементарное событие, принадлежащее пространству , т. е. .

В приложениях нас обычно интересуют не сами случайные величины, а вероятности некоторых событий, связанных со случайными величинами .

Например, какова вероятность того, что число выпавших очков на игральной кости равно четырем? Или больше четырех ?

Для того, чтобы мы могли найти такие вероятности, нужно знать распределение случайной величины.

Для дискретной случайной величины распределение удобнее всего задать в виде таблицы

(хотя можно и иначе - как?)

(такая таблица может быть и бесконечной)

Для любой дискретной случайной величины выполняется соотношение

Для непрерывной случайной величины невозможно составить перечень всех ее значений и построить ряд распределения. Поэтому для задания распределения непрерывной случайной величины вводится функция распределения.

4

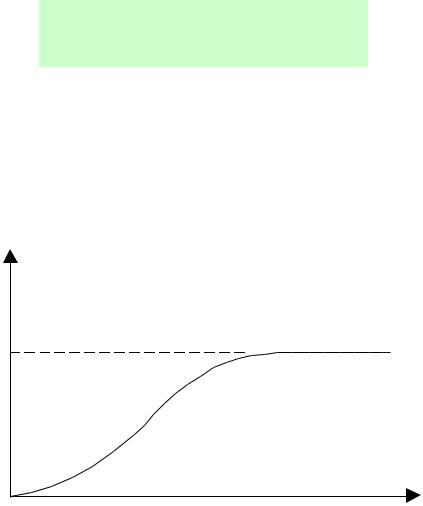
Функцией распределения случайной величины X или

интегральным законом распределения называется функция

F(x), равная вероятности того, что в результате опыта случайная величина примет значение, меньшее х, то есть

FX (x) P(X x) (0.2)

(индекс X у функции распределения писать не будем, если нам ясно, о какой сл.в идет речь)

Геометрически функция распределения F(x) есть вероятность того, что в результате опыта случайная точка X попадет левее х.

Функцию распределения можно построить и для дискретной случайной величины. Функция распределения любой дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величии ны, и равны вероятностям

5

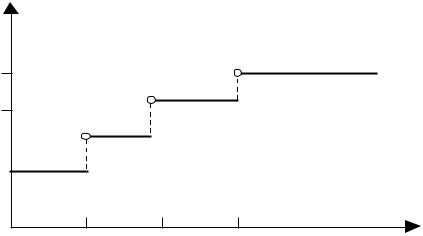
этих значений. Сумма всех скачков функции F(x) равна единице. Типичный вид функции распределения дискретной случайной величины приведен на рис. 0.2

F(x)

1

x

Рис. 0.2. Функция распределения дискретной случайной величины

Свойства функции распределения:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:

0 F(x) l.

2.Функция распределения случайной величины есть неубывающая функция на всей

числовой оси, т.е. при x2>х1

F(x2)>F(x1).

3.На минус бесконечности функция распределения равна нулю, на плюс бесконечности — единице, т.е.

6

4. Вероятность попадания случайной величины X в полуинтервал [х1,х2) равна приращению ее функции распределения на этом интервале, т.е.

Случайная величина X называется абсолютно непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Для непрерывной случайной величины X вероятность любого отдельно взятого значения равна нулю, т.е. P(X =x1) = 0, а вероятность попадания X в интервал (х1, х2) не зависит от того, является ли этот интервал открытым или закрытым (т.е., например, P(xl< x < х2) = P(хl X х2)).

Плотностью распределения f(х) абсолютно непрерывной случайной величины X называется производная ее функции распределения

Плотность распределения f(х), как и функция распределения F(х), дает один из способов задания распределения, но в отличие от функции распределения она существует только для абсолютно непрерывных случайных величин.

Свойства плотности распределения:

1.Плотность вероятности — неотрицательная функция, т.е. f(x)>0.

2.Вероятность попадания непрерывной случайной величины в интервал [a, b] равна определенному интегралу от ее плотности

7

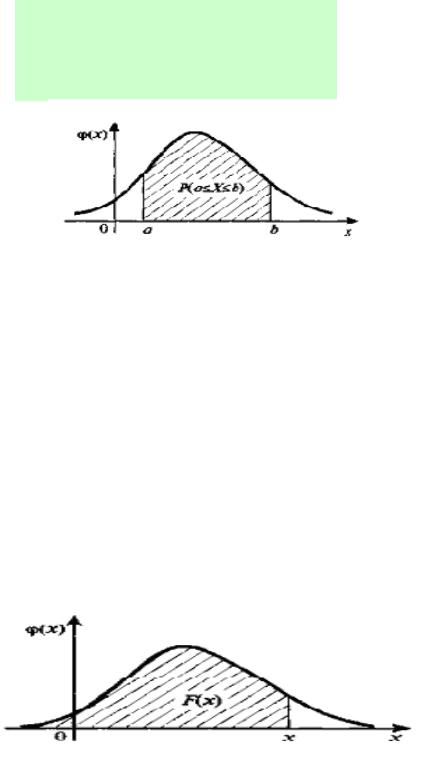
вероятности в пределах от а до b (см. рис. 2.2), т.е.

b

P(a X b) f (x)dx . (0.5)

a

Рис. 0.3. Вероятность попадания непрерывной случайной величины в интервал [a, b]

3. Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле:

В этом смысле значение функции распределения в точке x, т.е. F(x) является площадью под функцией плотности (x) до точки x.

Рис. 0.4. Функция распределения непрерывной случайной величины F(x) как интеграл от плотности (x)

Числовые характеристики случайных величин

8

где f(x) – плотность распределения X.

Здесь интеграл должен сходится абсолютно.

Свойства математического ожидания:

1)М(С) = С, где С — постоянная величина;

2)M(k X) = k M(X);

3)М(Х± Y) = М(Х) ± M(Y);

4)M(X Y) = M(X) M(Y), где X, Y —

независимые случайные величины;

5)М(Х± C) = М(Х)± С.

Дисперсией DX случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания:

DX M (X MX )2 , (0.9)

Дисперсия характеризует разброс, рассеяние значений сл.в. относительно своего среднего значения.

Часто для подсчета дисперсии используется следующая рабочая формула:

DX MX 2 (MX )2 (0.10)

Для дисперсии случайной величины X используется также обозначение Var(X), которое больше подходит для выражения ее смысла: дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений случайной величины относительно среднего значения (принято в англоязычной литературе).

10