§ 7. Непрерывные кривые |
|
|
|
|
||
Пусть параметр t принимает действительные значения |
||||||
на отрезке 0 6 t 6 1, и пусть каждому такому значению t |
||||||
поставлено в соответствие некоторое комплексное число |
|
|||||
|
z(t) = x(t) + iy(t). |
|
|
|
||
Плоскость, на которой изображаются значения z, мы бу- |
||||||
дем в дальнейшем называть просто «плоскость z». Если |
||||||
функции x(t) и y(t) непрерывны при 0 6 t 6 1, то при из- |
||||||
менении t от 0 до 1 точка z(t) будет описывать некото- |
||||||
рую непрерывную кривую на плоскости z. При этом мы |
||||||
будем рассматривать эту кривую |
|
|
|
|
||
с направлением, принимая |
точку |
|
|
|
|
|
z0 = z(0) |
за начальную, а точ- |
|
|
|
|
|
ку z1 = z(1) за конечную. Функ- |
|
|
|
|
||
цию z(t) мы будем называть па- |
|
|
|
|
||
раметрическим уравнением |
этой |
|
|
|
|
|
кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и м е р 16. Пусть z(t) = t + |
|
|
|
|
||
it2. Тогда x(t) = t и y(t) = t2. По- |
|
|
|
|
||
этому y(t) = x2(t) при любом t, т. е. |
||||||
точка z(t) при любом t лежит на |
|
Рис. 16 |
|
|||
параболе |
= 2. При изменении t от 0 до 1 x(t) также меня- |
|||||
ется от 0 до 1 и точка z(t) пробегает дугу параболы y = x2 |
||||||
от точки z0 = 0 до точки z1 = 1 + i (рис. 7). |
|
|
|
|||
244. Построить на плоскости z кривые, задаваемые |
||||||
следующими параметрическими уравнениями: a) z(t) = 2t; |
||||||
б) z(t) = it; в) z(t) = it2; г) z(t) = t − it; д) z(t) = t2 + it; |
||||||
e) z(t) = R(cos 2pt + i sin 2pt); ж) z(t) = R(cos 4pt + i sin 4pt); |
||||||
з) z(t) = R(cos pt + i sin pt); |
|
|
|
|
|
|
|
cos 2pt + i sin 2pt |
при 0 6 t 6 1/2, |
|
|
||
и) z(t) = 4t − 3 |
при 1/2 < t 6 1. |
|
|
|||
245. Написать какое-нибудь параметрическое уравнение |
||||||
отрезка, |
соединяющего |
точки |
z0 = a0 |
+ b0i |
и |
|
z1 = a1 + b1i. |
|
задачах |
параметриче- |
|||
З а м е ч а н и е. В последующих |
||||||
ские уравнения имеют индексы. Эти индексы указывают |
||||||
лишь на номер кривой, но рассматриваются данные кривые |
||||||
на одной и той же плоскости z. |
|
|
|
|
||
246. С помощью каких геометрических преобразований |
||||||
73
из кривой C1 с уравнением z1(t) получается кривая C2 с уравнением z2(t), если:
a) z2(t) = z1(t) + z0 (z0 — фиксированное комплексное число);
б) z2(t) = a · z1(t), где a — действительное положительное число;
в) z2(t) = z0 · z1(t), где |z0| = 1;
г) z2(t) = z0 · z1(t), где z0 — произвольное комплексное число?
247. Пусть z1(t) — параметрическое уравнение кривой C. Какая кривая описывается уравнением z2(t), если z2(t) =
z1(1 − t)?
248. Пусть z1(t) и z2(t) — параметрические уравнения кривых C1 и C2, и пусть z1(t) = z2(0). Какая кривая описывается уравнением z3(t), если
|
|
z |
(2t) |
|
при |
0 |
6 |
t |
6 |
1 |
, |
||
|
|
|
|||||||||||
z3(t) = |
1 |
|
|
|
1 |
|
2 |
|
|||||
|
z2 |
(2t |
− |
1) |
при |
|
|
< t 6 1? |
|||||
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
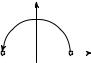
249.Пусть z(t) = cos pt + i sin pt (рис. 7). Найти все значения Arg z(t) в зависимости от t.
250.Пусть z(t) = cos pt + i sin pt. Как нужно выбрать одно из значений Arg z(t) при каждом t, чтобы выбранные
значения изменялись непрерывно при
изменении t от 0 до 1, при условии, что
|
|
Arg z(0) выбран равным: а) 0, б) 2p, |
|
|
в) −4p, г) 2pk (k — фиксированное це- |
|
|
лое число). |
Рис. 17 |
|
Следующее утверждение интуитив- |
но кажется достаточно очевидным, и мы приведем его без доказательства.
Те о р е м а 6. Пусть непрерывная кривая C с параметрическим уравнением z(t) не проходит через начало координат ( т. е. z(t) 6= 0 при 0 6 t 6 1), и пусть аргумент начальной точки кривой C (т. е. Arg z(0))выбран равным f0. Тогда можно так выбрать одно из значений аргумента для всех точек кривой C, чтобы при движении точки по кривой ее аргумент изменялся непрерывно, начиная со значения f0.
Другими словами, можно при каждом t выбрать f(t) —
74
одно из значений Arg z(t) так, чтобы функция f(t) была непрерывна при 0 6 t 6 1 и чтобы f(0) = f0*).
251.Пусть f(t) и f0(t) — две функции, описывающие непрерывное изменение Arg z(t) вдоль кривой C. Доказать, что f(t) − f0(t) = 2pk, где k — некоторое фиксированное целое число, не зависящее от t.
252.Доказать, что если выбрано некоторое значение
f(0) = f0, то функция f(t), описывающая непрерывное изменение Arg z(t) вдоль кривой C, определяется однозначно.
253.Пусть функция f(t) описывает непрерывное изменение Arg z(t). Доказать, что функция y(t) = f(t) − f(0) однозначно определяется функцией z(t) и не зависит от выбора f(0).
Из утверждения задачи 253 вытекает, в частности, при t = 1, что для данной непрерывной кривой C, не проходящей через точку z = 0, величина f(1) − f(0) однозначно определяется условием непрерывного изменения f(t).
О п р е д е л е н и е. Величину f(1) − f(0) будем называть
изменением аргумента вдоль кривой C.
254.Чему равно изменение аргумента вдоль кривых со следующими параметрическими уравнениями:
a) z(t) = cos pt + i sin pt, б) z(t) = cos 2pt + i sin 2pt, в) z(t) = cos 4pt + i sin 4pt, r) z(t) = (1 − t) + it?
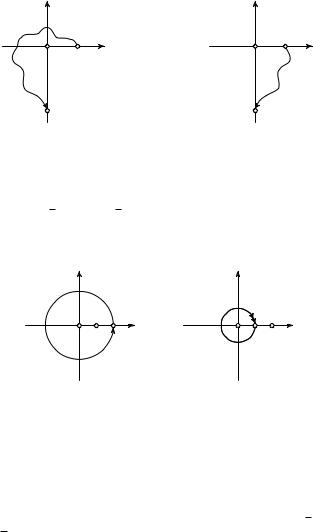
255. Чему равно изменение аргумента вдоль кривых, изображенных на рис. 18?
Если непрерывная кривая C замкнута, т. е. z(1) = z(0), то величина f(1) − f(0) имеет вид 2pk, где k — целое число.
О п р е д е л е н и е. Если для непрерывной замкнутой кривой C, не проходящей через точку z = 0, изменение аргумента равно 2pk, то будем говорить, что кривая C обходит k раз вокруг точки z = 0.
256. Сколько раз обходят вокруг точки z = 0 следующие кривые:
*) В книге: С т и н р о д Н., Ч и н н У., Первые понятия топологии, «Мир», 1967, §§ 20–23, строго и доступно определяется угол, заметаемый данной кривой. Используя это понятие, легко получить утверждение теоремы 6: достаточно положить f(t) = f0(t) + f1(t), где f1(t) — угол, заметаемый частью данной кривой от z(0) до z(t).
75
|
|
|
|
Рис. 18
а) z(t) = 2 cos 2pt + 2i sin 2pt (рис. 19),
б) z(t) = 12 cos 4pt − 12 i sin 4pt (рис. 20), в) кривая на рис. 21,
г) кривая на рис. 22?
|
|
|
|
Рис. 19 |
Рис. 20 |
257.Доказать, что число обходов непрерывной замкнутой кривой вокруг точки z = 0 не зависит от выбора начальной точки, а зависит только от направления кривой.
258.Пусть кривая C с уравнением z1(t) обходит k раз вокруг точки z = 0. Сколько раз обходит вокруг точки z = 0
кривая с уравнением z2(t), если: a) z2(t) = 2 · z1(t); б) z2(t) = = −z1(t); в) z2(t) = z0 · z1(t), где z0 6= 0; г) z2(t) = z1(t),
где z — число сопряженное z?
О п р е д е л е н и е. Пусть замкнутая непрерывная кривая C с уравнением z1(t) не проходит через точку z = z0. Тогда будем говорить, что кривая C обходит k раз вокруг точки z0, если кривая с уравнением z2(t) = z1(t) − z0 обходит k раз вокруг точки z = 0 (рис. 23).
76