Глава 4

Аналитическая геометрия на плоскости и в пространстве

§29. Прямая на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой и его исследование

29.1 Общее уравнение прямой на плоскости

Определение 29.1: Под прямой линией будем понимать геометрическое место точек l такое, что для любых двух точек M и M из данного множества вектор коллинеарен заданному ненулевому вектору .

Или .

Получим уравнение прямой линии на плоскости (то есть получим такое уравнение, которому должны удовлетворять координаты всех точек на прямой линии l и наоборот, если координаты некоторой точки удовлетворяют составленному уравнению, то эта точка лежит на прямой l).

Пустьи (29.1)

Рассмотрим следующие случаи:

1. = 0. Тогда оси ординат OY, и первая координата x-x пропорциональна нулю, т.е.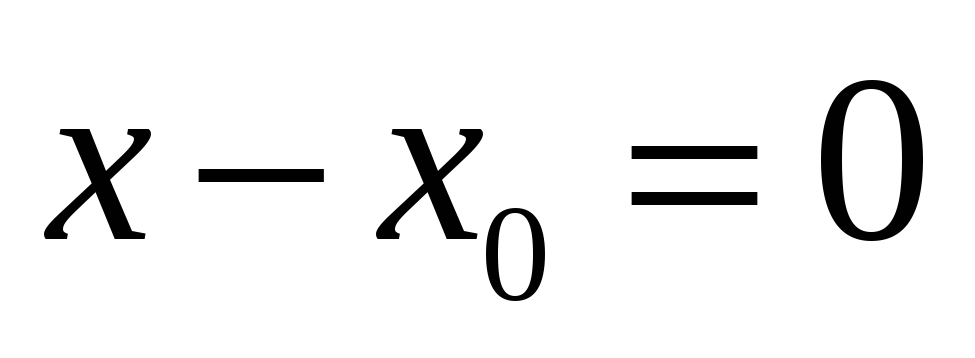 (в этом случае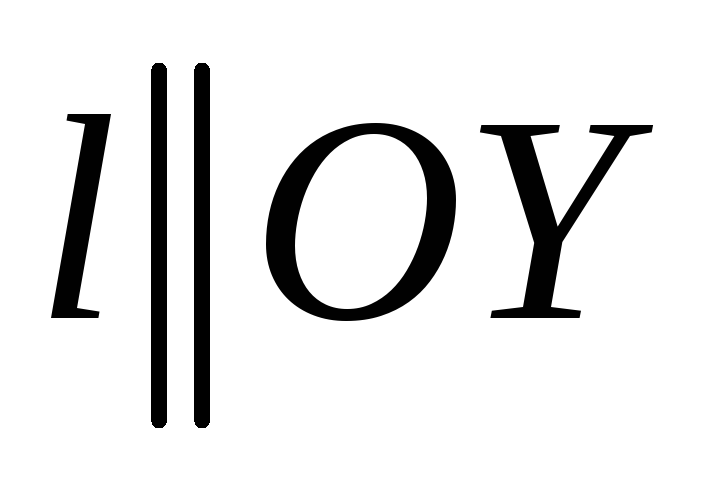) (29.2)

2. = 0. Тогда 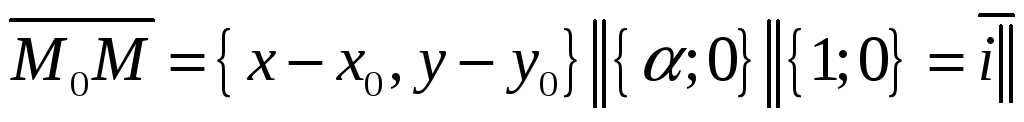оси абсцисс OX, и вторая координата 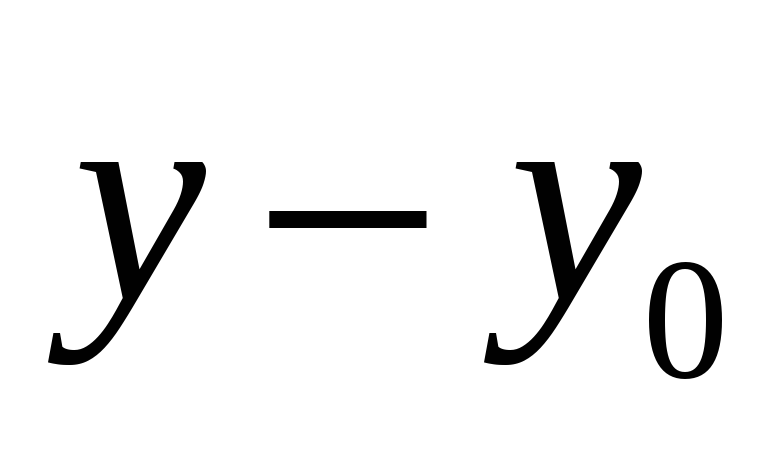пропорциональна нулю, то есть 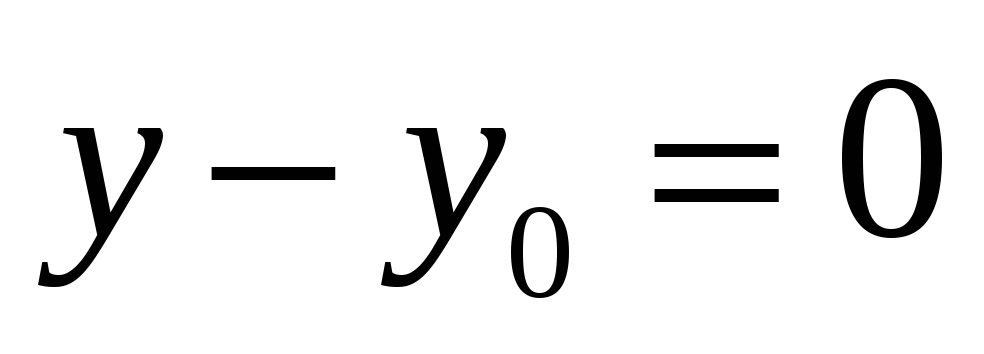(в этом случае 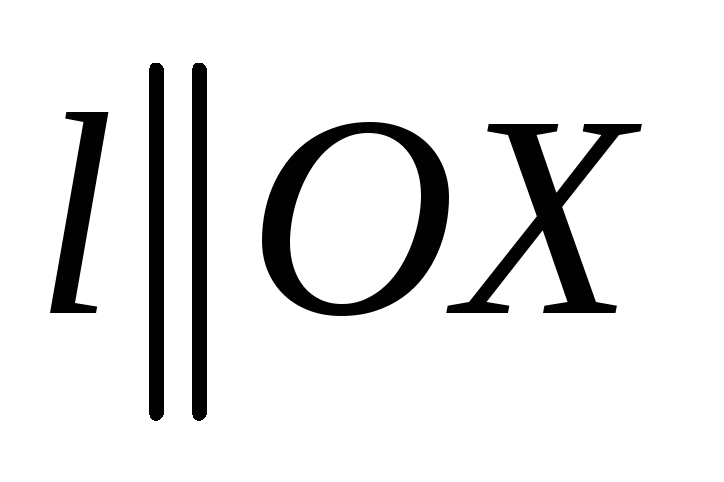) (29.3)

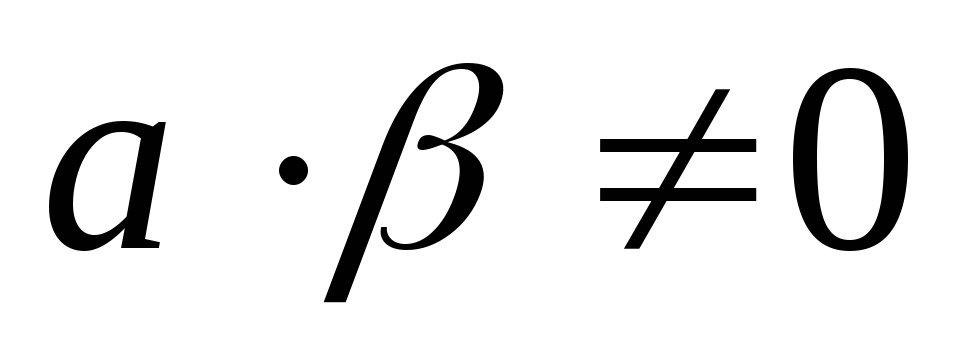3. Так как 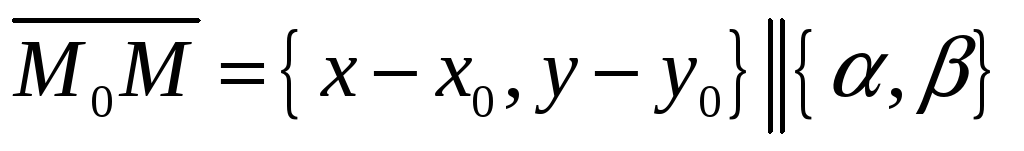, то или 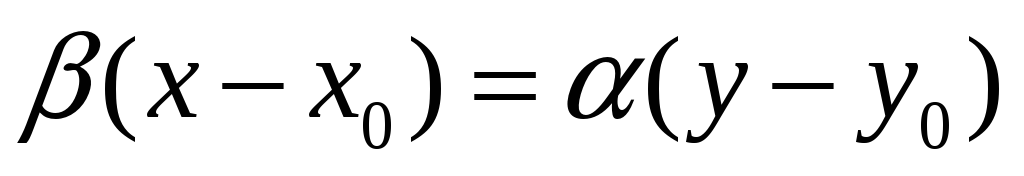(29.4)

Раскрывая скобки и перенося все слагаемые в уравнении (29.4) в левую часть, получим. Положив и , из последнего уравнения имеем (при этом (см.(29.1)).

(29.5)

и (29.6)

Отметим, что уравнения (29.2) (при A=1, B=0, C=) и (29.3) (тогда A=0, B=1, C=) является частичными случаями уравнения (29.5) с условием (29.6). Итак, мы показали, что если точка M принадлежит некоторой прямой l, то её координаты удовлетворяют некоторому уравнению (29.5) с условием (29.6) на коэффициенты A и B.

Покажем обратное, то есть если координаты всех точек M удовлетворяющих некоторому уравнению (29.5) с условием (29.6), то эти точки лежат на некоторой прямой l (удовлетворяющей определению 29.1).

ЗАДАЧА. Доказать, что если векторы и ортогональны некоторому вектору , то и коллинеарные.

Для её решения заметим, что координаты векторов и должны удовлетворять уравнению Ax+By=0, которое (см §17,18,19) является линейным пространством размерности 1 и, следовательно, всякие два решения этого уравнения линейно зависимы. Далее - §16.

Заметим, что уравнение (29.5) имеет решения(например, если (см.(29.6)), то координаты точек удовлетворяют уравнению (29.5).

Пусть и M(x,y) – любые решения уравнения (29.5), то есть:

(29.5)

и (29.7)

Вычитая из уравнения (29.5) уравнение (29.7), получим

(29.8)

Это означает, что вектор ортогонален вектору (см.(29.6)). Но и вектор также ортогонален вектору , потому что и скалярное произведение (см. §24). Поэтому то есть точки и М находятся на некоторой прямой линии l. Таким образом, уравнение (29.5) с условием (29.6) задает некоторую прямую линию l на плоскости и наоборот, всякую линию l на плоскости можно описать некоторым уравнением (29.5) с условием (29.6).

Определение 29.2: Уравнение (29.5) с условием (29.6) называется общим уравнением прямой линии на плоскости.

Определение 29.3: А векторназывается нормальным вектором (или нормалью) к прямой l, заданной уравнением (29.5).

Как уже было показано, вектор, то есть

29.2 Исследование общего уравнения прямой на плоскости

Исследуем общее уравнение прямой:

Ax+By+C=0 (29.5)

с условием (29.6)

Рассмотрим поочередно случаи, когда коэффициенты в уравнении (29.5) равны или не равны нулю – всего 5 частных случаев (когда один или два коэффициента в (29.5) обращаются в ноль; случаи A=B=0 и A=B=C=0 не удовлетворяют условию (29.6)) и один общий случай (когда все коэффициенты в (29.5) отличны от нуля).

Частный случай	Уравнение прямой	Особенность поведения прямой	Обоснование
1.A=0	y= -C/B	Прямая l коллинеарна оси абсцисс OX	См. уравнение (29.3)
2.B=0	x= -C/A	прямая l коллинеарна оси ординат OY	См. уравнение (29.2)
3.C=0	Ax+By=0	, то есть прямая l проходит через начало координат	При C=0 координаты точки удовлетворяют уравнению (29.5)
4.A=C=0	y=0	, то есть прямая является осью абсцисс	Сопоставим случаи 1. и 3., О(0;0) OX
5.B=C=0	x=0	, то есть прямая является осью ординат	Сопоставим случаи 2. и 3. точка O(0;0) OY

6. ABC 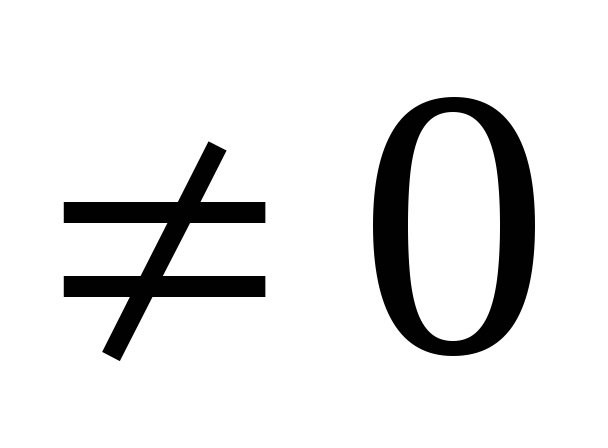(достаточно общий случай).

Тогда, поделив обе части уравнения (29.5) на « -С», получим . Обозначив за и , из последнего уравнения имеем

(29.9)

К уравнению (29.9) мы ещё вернемся в §31.

29.3 Уравнение прямой с угловым коэффициентом

Пусть (то есть прямая l не коллинеарна оси ординат (см.(29.2)). Тогда, поделив обе части уравнения (29.5) на «-В», получим

Положив и , из последнего уравнения имеем (29.10)

Найдем геометрический смысл коэффициентов k и b в уравнении (29.10). Положив x=0, из (29.10) находим y=b, а в случае y=0, будет. То есть точки и находятся на прямой .

Пусть – угол, под которым прямая l пересекает ось OX. Тогда

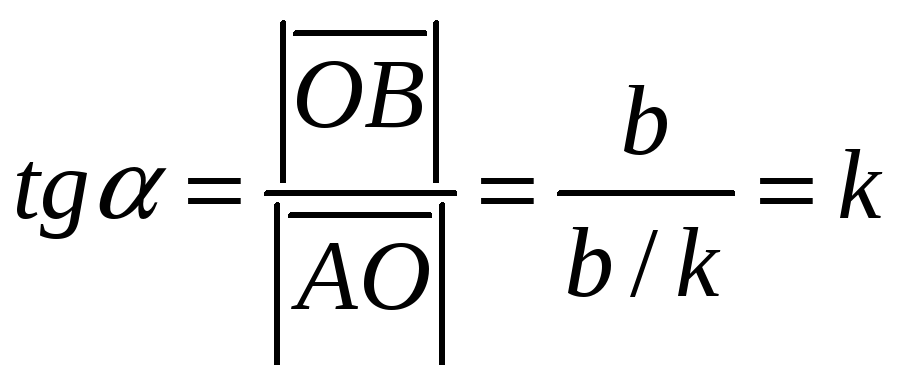(29.11) (см. чертеж 29.1)

рис.29.1

0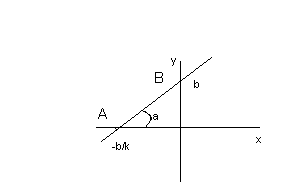

Из уравнения (29.11) имеем, что величина в уравнении (29.10) является тангенсом угла наклона прямой l к оси абсцисс ОХ.

Определение 29.4: Поэтому уравнение (29.10) называется уравнение прямой с угловым коэффициентом (а множитель k- её угловым коэффициентом).

К уравнению 29.10 можно свести всякую прямую, не коллинеарную оси ординат (если OY, то есть lOX , то и ).

Отметим, что в отличие от уравнения (29.5) (см. § 30), уравнение (29.10) однозначно определяет прямую l.

§30. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых

30.1 Случай уравнения прямых с угловыми коэффициентами

l 1

l 2

Р



ассмотрим прямые:



П



ри этом (см.(29.11)):

рис.30.1

Т

l1

ак как внешний угол в треугольнике, внутренними углами которого являются и (см. черт. 30.1, 30.2) то ( – угол между прямыми и ) (30.3) . Тогда из равенства (30.3) имеем



2

l2

Поэтому:

(30.4)

То есть угол между прямыми и можно найти по формуле (30.4).

рис.30.2

Рассмотрим взаимное расположение прямых и.

1. Условие параллельности: (см. черт. 30.2) (30.5)

(и , иначе )

2. Условие перпендикулярности: (см. чертеж 30.1) (см. равенство(30.4)) (30.6)

3.Точка пересечения прямых и .

Абсциссу точки пересечения прямых можно найти приравняв, правые части уравнений (30.1) и (30.2):

Решая уравнение (30.7), получим

А подставив полученную в (30.8) абсциссу точки пересечения прямых в уравнение (30.1) (или в (30.2)), найдем и ординату их точки пересечения :

=