
А. Р. Лакерник. Высшая математика.Краткий курс
.pdf
5. Дифференциальные уравнения
Как было показано там же, характеристическое уравнение дл я соответствующего (15.29) однородного уравнения имеет вид Φ(k + α) = 0 ,
r |
|
|
~ |
(k)= F(k + a) , последнее |
èëè k |
F (k + α) = 0 . Введя новый многочлен F |
|||
уравнение можно записать в виде |
|
|||
|
|
k |
r ~ |
(15.30) |
|
|
F (k) = 0, |
||
~ |
|
= F (a) ¹ 0 . |
|
|
ãäå F (0) |
|
|
||
Значит, 0 является корнем характеристического уравнения ( 15.30) кратности r, и в соответствии с п. а, частное решение (15.29) можно искать в виде u = xrQk (x), ãäå Qk (x) – многочлен степени k с неопределенными коэффициентами. Отсюда частное решение (15.26) можно искать в виде
y = xrQ |
(x)eαx. |
(15.31) |
k |
|
|
Подставляя функцию (15.31) в уравнение (15.26) и сокращая это уравнение на eαx , получим тождественное равенство (на R) двух многочленов степени k. Необходимым и достаточным условием такого равенства является совпадение коэффициентов этих многочл енов при одинаковых степенях x. Приравнивая эти коэффициенты, получим систему ( k +1) уравнений с ( k +1) неизвестными, которая, как можно доказать, всегда имеет единственное решение.
Таким образом, если f (x) = Pk (x)eαx , то частное решение неоднородного уравнения (15.26) ищется по формуле (15.31), в которой Qk (x) – многочлен степени k с неопределенными коэффициентами, r кр атность α как корня характеристического уравнения для соответствующего однородного уравнения (15.27), или сколько раз α , взятое из правой части уравнения (15.26), встречается среди корней характеристического уравнения.
Пример. Решить дифференциальное уравнение y¢¢ + y¢ - 2y = (6x - 1)ex . Ð å ø å í è å
Характеристическое уравнение для соответствующего одно родно-
го уравнения имеет вид k2 + k - 2 = 0 . Корни этого уравнения |
k = -2 |
, |
||
|
|
|
1 |
|
k = +1 |
, и общее решение однородного уравнения |
y = c e−2x + c ex . Òå- |
||
2 |
|
1 |
2 |
|
перь ищем частное решение исходного уравнения: a = 1 , r = 1 , k = 1 и y = x(Ax + B)ex = (Ax2 + Bx)ex .
Находим производные этой функции и подставляем в исходно е уравнение (для удобства записи опускаем символ *):
15. Линейные дифференциальные уравнения высших порядков
y¢ = (2Ax + B)ex + (Ax2 + Bx)ex = (Ax2 + (2 A + B)x + B)ex ;
y¢¢ = (2Ax + 2A + B)ex + (Ax2 +(2A + B)x + B)ex = ( Ax2 +(4 A + B) x + 2 A + 2B)ex;
(Ax2 + (4A + B)x + 2A + 2B)ex + (Ax2 + (2A + B)x + B)ex - 2( Ax2 + Bx)ex = = (6x -1)ex ;
Ax2 + 4Ax + Bx + 2A + 2B + Ax2 + 2Ax + Bx + B - 2Ax2 - 2Bx = 6x -1;
6Ax + 2A + 3B = 6x -1.
Приравнивая коэффициенты при одинаковых степенях в лево й и правой частях этой формулы, имеем
x1 : ì6A = 6;
x0 : íî2A + 3B = -1.
Из этой системы A = 1; 3B = -1- 2 = -3; B = -1. В итоге,
|
|
y = y + y = c e−2x + c ex + x(x -1)ex . |
|
|||||
|
|
|
1 |
2 |
|
|
|
|
2) |
f (x) = eαx éP |
(x)cosbx +Q |
(x)sinbxù |
, ãäå |
P |
(x) è Q |
(x) – ìíî- |
|
|
ë |
k |
m |
û |
|
k |
m |
|
гочлены степени k и m соответственно с действительными коэффициентами (это обобщение случая 1, который получается отсюда п риβ = 0 ).
Покажем, что в этом случае частное решение неоднородного уравнения (15.26) следует искать по формуле
y = xreαx éR |
(x)cosbx +T |
(x)sinbx ù, |
(15.32) |
ë l |
l |
û |
|
ãäå Rl (x) è Tl (x) – многочлены степени l с неопределенными (действительными) коэффициентами, l = max{k,m}, r – кратность (α + iβ) как корня характеристического уравнения для соответствующе го однородного уравнения (15.27), или сколько раз (a + ib), взятое из правой части уравнения (15.26), встречается среди корней характеристического уравнения .
Для этого заменим в функции f (x) cosβx и sinbx на их выражения через показательные функции:
|
α |
x |
é |
|
|
|
|
|
|
eiβx |
+ e−iβx |
|
|
|
eiβx - e−iβx |
ù |
|
|
||||
f (x) = e |
ê |
P |
(x) |
|
|
|
|
+Q |
(x) |
|
|
|
ú |
= |
||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
2 |
|
|
m |
|
|
|
2i |
|
|
|
||
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
||
|
éP (x) |
|
Q (x)ù |
|
|
éP (x) |
|
Q (x)ù |
||||||||||||||
= e(α+iβ)x |
ê |
|
k |
|
|
|
+ |
|
|
m |
|
ú |
+ e(α−iβ)x ê |
|
k |
- |
m |
|
|
ú. |
||
|
2 |
|
|
|
|
2i |
|
|
2 |
2i |
|
|
||||||||||
|
ë |
|
|
|
|
|
|
û |
|
|
ë |
|
|
|
û |
|||||||
302 |
303 |

5. Дифференциальные уравнения
Обозначим в |
|
этой формуле |
Pk (x) |
+ |
Qm(x) |
= F (x) , тогда |
||||||||
2 |
2i |
|||||||||||||
Pk (x) |
|
|
Qm(x) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
, ãäå |
|
– комплексно сопряженное число к |
|||||||
- |
|
= F (x) |
F (x) |
|||||||||||
2 |
2i |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
F(x); оба многочлена (с комплексными коэффициентами) F(x) и F(x) имеют степень l. Отсюда
f (x) = F(x)e(α+iβ)x + |
|
e(α−iβ)x. |
(15.33) |
F(x) |
К этой правой части применимы рассуждения разд. 15.5 и п. 1 этого раздела (они справедливы и для комплексных коэффициен тов многочленов и показателей степеней числа e).
В соответствии с теоремой 15.5 частное решение уравнения L(y) = f (x) , где f(x) – задана формулой (15.33), есть сумма частных решений двух уравнений:
L(y) = F (x)e(α+iβ)x è L(y)= F (x)e(α−iβ)x.
Пусть y1 – частное решение первого из них, т.е.
a y(n) + a y(n−1) |
+ ...+ a |
y¢ |
+ a y |
= F(x)e(α+iβ)x . |
|
0 1 |
1 1 |
n−1 |
1 |
n 1 |
|
Применим к обеим частям этого равенства операцию сопряже ния. Учитывая действительность коэффициентов ai , òî, ÷òî z1 + z2 = z1 + z2 , z1z2 = z1 × z2, а значит,
e(α+iβ)x = eαx × eiβx = eαx (cosbx + i sinbx) =
= eαx (cosbx - i sinbx) = eαx ×e−iβx = e(α−iβ)x
è
|
|
|
lim |
y(x + Dx) - y(x) |
= |
lim |
y(x + Dx) - y(x) |
= |
|||||||||
|
y¢ = |
||||||||||||||||
|
|
|
|
|
|
Dx |
|||||||||||
|
|
|
x→0 |
Dx |
|
|
|
x→0 |
|
|
|
||||||
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
||||
|
|
|
|
= lim |
y(x + Dx) |
y(x) |
= y¢, |
|
|||||||||
|
|
|
|
Dx |
|
|
|
|
|
|
|||||||
имеем |
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a y (n) + a y (n−1) + |
...+ a |
y ¢ + a y |
|
= |
|
e(α−iβ)x , |
|||||||||||
|
F(x) |
||||||||||||||||
0 1 |
|
1 1 |
n−1 |
|
1 n 1 |
|
|
|
|
||||||||
ò. å. y1 является частным решением второго из этих уравнений.
15. Линейные дифференциальные уравнения высших порядков
Согласно выводам п. 1, y1 следует искать в виде y1 = xrUl (x)e(α+iβ)x , ãäå Ul (x) – многочлен степени l, r – кратность ( a + ib ) как корня характеристического уравнения для соответствующего однор одного уравнения (15.27). Тогда
y1 = xrU l (x )e(α+iβ)x = xrU l (x )e(α – iβ)x,
èчастное решение уравнения L(y) = f (x) с правой частью (15.33) следует искать в виде
y*= y1 + y1 =xrU l (x)e(α+iβ)x +xrU l (x)e(α – iβ)x =
= xrUl (x)eαx(cosbx +i sinbx) + xrU l (x)e αx(cosbx -i sinbx ) =
= xreαx éë(Ul (x) +Ul (x))cosbx + i((Ul (x) -Ul (x))sinbxùû. (15.34) Пусть
|
|
|
|
l |
|
|
|
|
|
|
|
|
||
|
|
|
Ul (x) = åbk xl−k = b0xl + b1xl−1 + ... + bl , |
|||||||||||
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
||
где коэффициенты b0 ¹ 0, b1,..., bl |
– некоторые (комплексные) числа, |
|||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
||||
тогда |
|
= å |
|
xl−k . Введем многочлены |
||||||||||
Ul (x) |
bk |
|||||||||||||
|
|
k=0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
l |
|||||
|
|
|
Rl (x) =Ul (x) + |
|
|
= å(bk + |
|
|
)xl−k ; |
|||||
|
|
|
Ul (x) |
bk |
||||||||||
|
|
|
|
|
|
|
|
|
k=0 |
|||||
|
|
|
|
|
|
|
|
|
l |
|
|
|||
|
|
Tl (x) = i(Ul (x) -Ul (x)) = åi(bk - bk )xl −k . |
||||||||||||
|
|
|
|
|
|
|
|
|
k=0 |
|||||
Òàê êàê z + z = x + iy + x - iy = 2x |
è i(z - z |
) = i(x + iy - x + iy) = -2y , òî |
||||||||||||
оба этих многочлена имеют действительные коэффициенты и степени, не превышающие l, причем степень хотя бы одного из этих много- членов равна l (есëи в обоих мноãîчленах x в старшей степени l ñîêðà-
ùàåòñÿ, òî b0 + b0 = 0 è i(b0 - b0) = 0 , |
откуда следует: b0 + b0 = 0 , |
b0 - b0 = 0 , значит, b0 = 0 , что противоречит условию). |
|
Подставляя Rl (x) è Tl (x) в формулу (15.34), получаем |
|
y = xreαx[R (x)cosbx +T (x)sinbx], |
|
l |
l |
т.е. формулу (15.32).
304 |
305 |

5. Дифференциальные уравнения
При подстановке решения вида (15.32) в уравнение (15.26) после сокращения на eαx получаем тождественное равенство (на R) двух функций. Приравнивая коэффициенты при xi cosβx è x j sinβx в обеих ча- стях этого равенства (такие функции линейно независимы), п олучаем систему уравнений, из которой единственным образом наход им коэффициенты многочленов Rl (x) è Tl (x).
Пример. Решить диффененциальное уравнение y¢¢¢ + y¢ = sin2x . Р е ш е н и е
Соответствующее однородное уравнение y¢¢¢ + y¢ = 0 . Его характеристическое уравнение имеет вид k3 + k = 0 , èëè k(k2 + 1) = 0 . Отсюда k1 = 0 è k2,3 = ±i . Общее решение исходного уравнения: y = c1 + c2 cos x + c3 sin x .
Частное решение исходного уравнения: Pk (x) = 0 , Qm(x) = 1, k = m = 0 ; a = 0 , b = 2 , a + bi = 2i ; это число не является корнем характеристическо-
го уравнения, поэтому r = 0 и y = A cos2x + B sin 2x . Отсюда (символ * для удобства записи опускаем)
y¢ = -2Asin2x + 2B cos2x , y¢¢ = -4Acos2x - 4B sin2x , y¢¢¢ = 8Asin2x - 8B cos2x.
Подставляем в исходное уравнение:
8Asin2x - 8B cos2x - 2Asin2x + 2B cos2x = sin2x; 6Asin2x - 6B cos2x = sin2x.
|
Приравниваем коэффициенты при cos2x и sin2x : íì-6B = 0; |
Отсюда |
|||
|
|
|
|
î 6A = 1. |
|
A = |
1 |
, B = 0 è |
y = y + y = c1 + c2 cosx + c3 sin x + |
1 cos2x. |
|
|
6 |
|
|
6 |
|
Этот пример еще раз подтверждает, что независимо от налич ия в правой части линейного дифференциального уравнения обе их функций – cosβx è sinβx или только одной из них, в решении вида (15.32)
должны присутствовать обе эти функции.
Замечание. Если правая часть уравнения (15.26) является суммой двух или большего числа функций специального вида, то для нахо ждения частного решения этого уравнения удобно использовать упомян утую выше теорему 15.5.
15. Линейные дифференциальные уравнения высших порядков
15.7. Метод вариации произвольных постоянных
Теперь вернемся к общему виду линейного неоднородного ди фференциального уравнения. Пусть
L(y) = y(n) + p (x)y(n−1) |
+ p (x)y(n−2) |
+ ...+ p (x)y , |
(15.34) |
1 |
2 |
n |
|
а неоднородное и соответствующее однородное уравнения и меют вид
y(n) + p (x)y(n−1) |
+ p (x)y(n−2) + |
...+ p (x)y = f (x), x (a,b) |
(15.35) |
1 |
2 |
n |
|
y(n) + p (x)y(n−1) + p (x)y(n−2) |
+ ...+ p (x)y = 0, x (a,b). |
(15.36) |
|
1 |
2 |
n |
|
Общее решение уравнения (15.35) имеет вид |
|
||
|
y = y + y , |
(15.37) |
|
ãäå |
|
|
|
|
y = c1y1 + c2y2 + ... + cnyn – |
(15.38) |
|
общее решение уравнения (15.36) ( y1, y2,..., yn – фундаментальная система решений этого уравнения), а y – частное решение уравнения (15.35).
Метод вариации произвольных постоянных заключается в на хождении y по той же формуле (15.38), считая, что в ней коэффициенты ci являются функциями x : ci = ci (x), i = 1, 2,..., n.
При подстановке такой функции в уравнение (15.35) получим одн о уравнение с n неизвестными: c1,c2,...,cn . Остальные n −1 уравнения мы допишем наиболее удобным для нас способом. Имеем
pn(x) |
|
|
|
y = c1y1 + ...+ cn yn |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y |
′ |
|
′ |
|
′ |
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
pn−1(x) |
|
|
= c1y1 + ...+ cn yn |
+ c1y1 |
+ ...+ cn yn. |
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||
Потребуем, чтобы c′y |
+ |
...+ c′ y |
|
= 0 – это 1-е уравнение. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
n n |
|
|
|
|
|
p |
(x) |
|
y′′ = c y′′+ ...+ c |
y |
′′ + c′y′ |
+ ... + c′ y′ . |
|
|
||||||||||
|
|
|
||||||||||||||||
n−2 |
|
|
|
|
|
|
|
|
|
1 1 |
n n 1 1 |
|
n n |
|
|
|||
Потребуем, чтобы c′y′ |
+ |
...+ c′ y′ |
|
= 0 – это 2-е уравнение. И т.д. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
n n |
|
|
|
|
|
p1(x) |
|
|
|
|
y |
(n−1) |
(n−1) |
|
|
(n−1) |
′ (n−2) |
′ (n−2) |
. (15.39) |
|||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
= c1y1 |
+ ...+ cn yn |
|
|
+ c1y1 |
+ ...+ cnyn |
|||||||
306 |
307 |

5. Дифференциальные уравнения
Потребуем, чтобы c¢y(n−2) |
+ ...+ c¢ y(n−2) = 0 – это (n -1)-е уравнение: |
|||
1 |
1 |
n n |
|
|
y(n) = c y(n) + |
...+ c y(n) |
+ c¢y(n−1) |
+ ...+ c¢ y(n−1). |
|
1 |
1 |
n n |
1 1 |
n n |
Последнее n-е уравнение получается после подстановки всех этих функций в формулу (15.35). Для этого надо умножить последнее из равенств (15.39) на 1, предпоследнее – на p1(x), ..., второе – на pn−1(x), первое – на pn(x) (все эти множители приведены в столбце слева) и все полученные новые равенства сложить. Собрав вместе члены с c1,c2,...,cn , получим
L(y) = c1L(y1) + c2L(y2) +...+ cn L(yn ) +
|
+ c1¢ y1(n – 1) + c¢2 |
y2(n – 1) + cn¢ yn(n – 1) = f (x). |
(15.40) |
|||||||||
Òàê êàê y1, y2,..., yn решения (15.36), то L(y1) = 0 , L(y2) = 0 , ..., |
||||||||||||
L(yn) = 0, и уравнение (15.40) приобретает вид |
|
|
|
|||||||||
|
c¢y(n−1) + c¢ y(n−1) + ... + c¢ y(n−1) = f (x). |
(15.41) |
||||||||||
|
1 1 |
2 2 |
|
|
|
|
|
n n |
|
|
|
|
Теперь выпишем систему уравнений для ci¢ = ci¢(x): |
||||||||||||
|
ìc¢y |
+ c¢ y |
+ |
... + c¢ y |
n |
= 0; |
|
|
|
|||
|
ï 1 1 |
2 2 |
|
|
|
n |
|
|
|
|
|
|
|
ïc¢y¢ |
+ c¢ y |
+ |
... + c¢ y |
¢ |
= 0; |
|
|
|
|||
|
ï 1 1 |
2 2 |
|
|
|
n |
|
n |
|
|
|
|
|
................................................. |
|
|
|||||||||
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
ïc¢y(n−2) + c¢ y(n−2) |
+ ...+ c¢ y(n−2) |
= 0; |
(15.42) |
||||||||
|
ï 1 1 |
2 |
2 |
|
|
|
n n |
|
|
|
||
|
ïc¢y(n−1) + c¢ y(n−1) |
+ ...+ c¢ y(n−1) |
= f (x). |
|||||||||
|
î 1 1 |
2 |
2 |
|
|
|
n n |
|
|
|
||
Система (15.42) – это система n линейных уравнений с n неизвест- |
||||||||||||
íûìè c′,c′ |
,...,c′ . Систему легко запомнить, ее коэффициентами явля- |
|||||||||||
1 2 |
n |
|
|
|
|
|
|
, âî 2-ì – y¢ |
, y¢ |
,..., y¢ , â 3-ì – |
||
ются: в 1-м уравнении – y , y |
2 |
,..., y |
n |
|||||||||
|
|
1 |
|
|
|
|
|
1 |
2 |
n |
||
y¢¢, y¢¢, ... , y¢¢ и т. д.; правые части всех уравнений, кроме последнего (n- |
||||||||||||
1 2 |
n |
|
|
|
|
|
|
|
|
|
|
|
го), равны 0, а правая часть последнего уравнения равна f (x). Определитель системы (15.42) есть определитель Вронского W (x)
функций y1, y2,..., yn , который отличен от 0 во всех точках интервала (a, b), так как функции y1, y2,..., yn линейно независимы на этом интервале. Значит, система (15.42) имеет единственное решение c1¢ = c1¢(x), c2¢ = c2¢ (x),..., cn¢ = cn¢ (x).
308
15. Линейные дифференциальные уравнения высших порядков
Первообразные для этих функций и являются нужными нам коэффициентами в формуле (15.38).
Пример. Решить дифференциальное уравнение y¢¢¢ + 3y¢¢ + 2y¢ = ex1+1. Ð å ø å í è å
Соответствующее однородное уравнение имеет вид y¢¢¢ + 3y¢¢ + 2y¢ = 0 . Характеристическое уравнение для этого дифференциально го уравнения
k3 + 3k2 + 2k = 0 имеет корни k1 = 0 , k2 = -1 , k3 = -2 , а общее решение однородного уравнения – y = c1 + c2e− x + c3e−2x .
Теперь ищем частное решение y исходного уравнения по той же формуле, считая, что в ней ci = ci (x) , i = 1, 2, 3 . Система (15.42) в данном примере выглядит так:
ìc¢ |
c¢e− x |
+ |
c¢e−2x |
= |
0; |
|
|||||||
ï |
1 |
+ 2 |
|
|
3 |
|
|
|
|
||||
ï |
|
c¢e− x |
- |
2c¢e−2x |
= |
0; |
|
|
|||||
í- |
|
2 |
|
3 |
|
|
1 |
|
|||||
ïc¢e− x + 4c¢e−2x = |
|
|
|
. |
|||||||||
|
|
x |
|
||||||||||
ï |
2 |
|
|
|
3 |
|
|
e |
+ 1 |
||||
î |
|
|
|
|
|
|
|
|
|
||||
Складывая 2-е и 3-е уравнения, имеем |
2c¢e−2x = |
1 |
; |
c¢ |
= |
e2x |
. Ïîä- |
|||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
ex |
+1 |
|
3 |
|
2(ex + 1) |
|
|
ставляя это выражение во 2-е уравнение, получаем |
|
|
|
|
|
|
||||||||||||||||
|
|
-c¢e− x - |
|
|
1 |
|
|
= 0; c¢ |
= - |
ex |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
ex + 1 |
|
|
2 |
|
|
ex + 1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Подставляя c¢ |
è |
c¢ в 1-е уравнение, получаем: |
|
|
|
|
|
|
||||||||||||||
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1¢ = |
1 |
|
|
- |
|
|
1 |
|
= |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
ex + 1 |
2(ex + |
1) |
|
2(ex +1) |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Теперь находим сами коэффициенты ci (x) (при нахождении первообразных произвольные постоянные не пишем, так как определя ем лишь одно частное решение неоднородного уравнения):
|
|
|
|
|
c2 = -ò |
ex |
dx = -ò |
d(ex + 1) |
|
= - ln(ex + 1); |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
ex + 1 |
|
ex + 1 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
ò |
e2x |
|
|
1 |
ò |
exdex |
1 |
ò |
(ex + 1) -1 |
dex = |
|
|
|
||||||||||||||||||
|
|
|
c3 = |
|
|
dx |
= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
ex +1 |
2 |
ex +1 |
2 |
|
|
ex +1 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
1 |
|
d(ex + 1) |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= |
|
òdex - 2 ò |
|
|
|
|
|
= |
2 ex |
|
- 2 ln(ex + 1); |
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
ex + 1 |
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
dx |
|
1 |
|
(ex +1) - ex |
|
|
1 |
|
|
1 |
|
|
|
d(ex +1) 1 |
1 |
|
|||||||||||||||||||
c1 = |
|
ò |
|
= |
|
ò |
|
|
|
|
|
dx = |
|
òdx - |
|
|
ò |
|
= |
|
x - |
|
|
ln(ex + 1). |
||||||||||||||
2 |
ex + 1 |
2 |
|
|
ex +1 |
|
|
2 |
2 |
ex + 1 |
2 |
2 |
||||||||||||||||||||||||||
309

5. Дифференциальные уравнения
Значит, y = 12 x − 21 ln(ex + 1)− e− x ln(ex + 1)+ 21 e− x − 21 e−2x ln(ex + 1) è
y = c1 + c2e− x + c3e−2x + 12 x − 12 ln(ex + 1) − e− x ln(ex +1) + 12 e− x − 12 e−2x ln(ex +1).
Легко понять, что если при нахождении первообразных будем прибавлять произвольные постоянные, то формула (15.38) при ci = ci (x) сразу даст общее решение исходного неоднородного уравнения.
Метод вариации произвольных постоянных в принципе приме ним для любых линейных неоднородных уравнений (даже с коэффи циентами, зависящими от x). Однако для произвольных таких уравнений нет общего метода решения соответствующих однородных уравн ений, поэтому этот метод применяется для решения уравнений с постоянны ми коэффициентами и правой частью, не являющейся функцией сп ециального вида. При правых же частях специального вида применяется боле е простой (в частности, не содержащий операции интегрирования) метод, изложенный в разд. 15.6.
310

VI
ÐßÄÛ
«
16.ЧИСЛОВЫЕ РЯДЫ
16.1.Свойства сходящихся рядов
Определение 16.1. Пусть дана последовательность∞чисел {an}. Составленный из этих чисел символ a1 + a2 + ...+ an + ... = åan называется
n=1
числовым рядом, а числа an называются членами этого ряда. Сумма n первых членов ряда называется n-й частичной суммой ряда и обознача-
ется S . Если существует конечный lim S |
n |
= S , то ряд называется схо- |
|||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||
дящимся (или ряд сходится), а число S – суммой ряда. В таком случае |
|||||||||||||||||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
часто пишут åan = S. В противном случае ( limSn = ∞ или не существу- |
|||||||||||||||||||||||
|
|
n=1 |
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|||||
ет) ряд называется расходящимся (или ряд расходится). |
|
||||||||||||||||||||||
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Èòàê, ðÿä åan |
сходится, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S :ε > 0 N = N(ε): n > N ( |
|
Sn − S |
|
< ε). |
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
||
|
Пример. Найти сумму геометрической прогрессии åb1qn . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Ð å ø å í è å |
|
|
|
|
|
|
|
n=0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Как известно из курса средней школы, |
|
|
Sn = |
b1(1 |
- qn ) |
и конечный |
||||||||||||||||
|
|
|
1 |
- q |
|||||||||||||||||||
|
|
b1(1 |
- qn ) |
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|||||||
lim Sn = lim |
= |
|
|
существует при |
|
q |
|
< 1; ïðè |
|
q |
|
> 1 этот предел |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||
1 |
- q |
1 |
- q |
|
|
|
|
||||||||||||||||
n→∞ |
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
бесконечен; при q = 1 ряд имеет вид b1 + b1 + b1 + ..., следовательно, Sn = nb1
è |
|
limSn = ¥ , при q = -1 ряд имеет вид b1 - b1 + b1 - b1 + ... , следовательно, |
||||||
|
|
n→∞ |
|
|
|
|
|
|
S |
|
= b |
при n нечетном и S |
|
= 0 при n четном и limS |
|
не существует |
|
|
n |
1 |
|
n |
n→∞ |
n |
|
|
(b1 ¹ 0). Значит, геометрическая прогрессия сходится при |
|
q |
< 1 è ïðè ýòîì |
|||||
311

|
|
6. Ðÿäû |
|
|
|
S = |
b1 |
(это формула суммы бесконечно убывающей геометрической |
1− q |
прогрессии).
Укажем ряд свойств числовых рядов.
Пусть дан ряд
∞
åan. (16.1)
n=1
Рассмотрим ряд, полученный из ряда (16.1) путем отбрасывания конечного числа его первых членов:
∞ |
|
å an. |
(16.2) |
n=k+1
Ряд (16.2) называется остатком ряда (16.1) после k-го члена.
Теорема 16.1. Ряды (16.1) и (16.2) сходятся или расходятся одновременно (т.е. сходимость ряда не зависит от поведения коне чного числа его первых членов).
¡ Пусть, как обычно, Sn – n-я частичная сумма ряда (16.1), sn – n-я частичная сумма ряда (16.2). Тогда при n > k
Sn = Sk + σn−k . |
(16.3) |
В этой формуле k – число фиксированное, т.е. Sk – постоянная величина. Если теперь устремить n к бесконечности, то существование
конечного lim Sn (т.е. сходимость ряда (16.1)) равносильно существо-
n→∞
ванию конечного lim sn−k = lim sn (т.е. сходимости ряда (16.2)). x
n→∞ n→∞
Теорема 16.2. Пусть ряд (16.1) сходится и S – его сумма. Сумму (сходящегося) ряда (16.2) обозначим Rk. Тогда сумму ряда можно представить в виде суммыk-й частичной суммы ряда и суммы остатка после k-го члена.
¡ Переходя в обеих частях формулы (16.3) к пределу при n ® ¥ , имеем
∞ |
k |
∞ |
S = Sk + Rk , èëè åan = åan + |
å an.x |
|
n=1 |
n=1 |
n=k+1 |
В силу этого равенства определение сходимости ряда можно запи-
∞
ñàòü òàê: ðÿä åan сходится, если
n=1
16. Числовые ряды
"e > 0 |
|
|
|
|
|
æ |
|
|
∞ |
|
|
|
|
|
< e |
ö |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
$N = N (e): "n > N ç |
|
å |
a |
|
|
÷. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
ç |
|
|
|
k |
|
|
|
|
÷ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
è |
k=n+1 |
|
|
|
|
ø |
|
|
|
|
|
|
|||||
Здесь же отметим, что согласно критерию Коши сходимости п ос- |
||||||||||||||||||||||||
ледовательностей существование конечного lim S |
n |
равносильно вы- |
||||||||||||||||||||||
полнению условия |
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
"e > 0 $N = N (e): "n > N , |
|
"p = 1,2,... ( |
|
Sn+ p - Sn |
|
|
|
< e). |
||||||||||||||||
|
|
|
||||||||||||||||||||||
Или ряд (16.1) сходится |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
n+ p |
|
|
|
|
ö |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Û "e > 0 $N = N (e):"n > N , "p = 1,2,... ç |
|
|
å |
a |
|
|
|
< e÷. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
k |
|
|
÷ |
||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
è |
|
k=n+1 |
|
|
|
|
ø |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
||||
Теорема 16.3. Пусть сходятся ряды åan |
è åbn , а суммы их рав- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
n=1 |
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íû S è S соответственно. Тогда сходится и ряд å(a an + b bn ) , ãäå α è |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b – постоянные, а сумма его равна a S + b S . |
|
|
|
|
|
|
|
|
|
|
~ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
¡ Пусть sn – n-я частичная сумма этого ряда, а Sn è S n – n-å ÷àñ- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
, следовательно |
|||||
тичные суммы исходных рядов. Тогда sn = a Sn + bS n |
||||||||||||||||||||||||
существует конечный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim s |
|
= a limS |
|
|
|
~ |
|
|
|
|
|
|
|
|
~ |
|
x |
|
|
|
|
|||
n |
n |
+ b limS n = aS + bS . |
|
|
|
|
|
|||||||||||||||||
n→∞ |
|
n→∞ |
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема 16.4 (необходимый признак сходимости ряда). Если ряд |
||||||||||||||||||||||||
(16.1) сходится, то lim a |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n→∞ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
¡ an = Sn - Sn−1. Если ряд (16.1) сходится и сумма его равна S, то из |
||||||||||||||||||||||||
этого равенства следует, что lim a |
|
= lim S |
|
- lim S |
|
|
= S - S = 0. x |
|||||||||||||||||
|
|
|
n→∞ n |
n→∞ |
n |
|
n→∞ |
n−1 |
|
|
|
|
|
|
||||||||||
Следствие. Если lim a ¹ 0 , то ряд (16.1) расходится (так как если |
||||||||||||||||||||||||
|
|
n→∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бы он сходился, то lim a |
= 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n→∞ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∞ 1 |
Ниже будет доказано, что так называемый гармонический ряд |
ån |
|
|
||
расходится, хотя lim 1 |
|
n=1 |
= 0 , т.е. необходимый признак сходимости не |
||
n→∞ n |
|
|
является достаточным.
312 |
313 |

6.Ðÿäû
16.2.Ряды с неотрицательными членами
∞
В этом разделе рассматриваются ряды åan , ãäå an ³ 0,
n=1
Для таких рядов Sn+1 = Sn + an ³ Sn , т.е. последовательность
тичных сумм не убывает.
∞
Теорема 16.5 (сравнения). Пусть даны ряды åan (16.1),
n=1
∞
åbn
n=1
n = 1, 2,...
{Sn} ÷àñ-
(16.4)
è 0 £ an £ bn, n = 1, 2,... Тогда если ряд (16.4) сходится, то сходится и ряд (16.1), а если ряд (16.1) расходится, то расходится и ряд (16.4).
~ |
– его сумма. Пусть Sn |
è |
~ |
¡ Пусть сходится ряд (16.4) и S |
Sn – n-å |
частичные суммы рядов (16.1) и (16.4) соответственно. Тогда по усло-
|
~ |
~ |
|
}не убывает и $ |
~ |
~ |
~ |
~ |
Þ {S |
}ограни- |
|||
âèþ S £ S |
|
. Íî {S |
|
lim S |
|
= S |
Þ S |
|
£ S |
||||
n |
|
n |
|
n |
|
n→∞ |
n |
|
|
n |
|
n |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
чена сверху: Sn £ S |
. Но по теореме 2.10 всякая неубывающая, ограни- |
||||||||||||
ченная сверху последовательность имеет конечный предел , следователь-
íî, $ lim S , т.е. ряд (16.1) сходится.
n→∞ n
Если же теперь расходится ряд (16.1), то расходится и ряд (16.4), та к как если бы он сходился, то по уже доказанной первой части теоремы, сходился бы и ряд (16.1), что противоречит условию. x
Замечание. Так как по теореме 16.1 сходимость ряда не зависит от поведения конечного числа его первых членов, то для справед ливости теоремы сравнения достаточно, чтобы условие 0 £ an £ bn выполнялось для всех n, начиная с некоторого номера.
|
∞ |
|
|
|
Пример. Исследовать на сходимость ряд å lnn . |
|
|
||
|
n=1 |
n |
|
|
|
Ð å ø å í è å |
|
∞ |
|
Òàê êàê lnn > 1 |
|
|
1 |
|
и, как было отмечено выше, гармонический ряд |
å |
|||
n n |
|
|
= |
n |
расходится, то исходный ряд тоже расходится. |
|
n 1 |
|
|
|
|
|
||
Выполнение условия 0 £ an £ bn часто зависит от не слишком существенных причин, поэтому вместо теоремы 16.5, как правило, удо бнее следующая теорема.
314
16. Числовые ряды
Теорема 16.6 (сравнения в предельной форме). Пусть даны ряды с
|
|
∞ |
∞ |
|
|
неотрицательными членами åan |
(16.1) è åbn (16.4) и пусть суще- |
||||
|
an |
n=1 |
n=1 |
|
|
ствует lim |
= K, где K ¹ 0, K ¹ ¥. Тогда ряды (16.1) и (16.4) сходятся |
||||
|
|||||
n→∞ bn |
∞ |
∞ |
|||
или расходятся одновременно (что обозначается как åan ~ åbn ). Ïðè |
|||||
|
|
|
n=1 |
n=1 |
|
K= 0 из сходимости ряда (16.4) следует сходимость ряда (16.1), а при
K= ¥ из расходимости ряда (16.4) следует расходимость ряда (16.1).
¡Пусть ряд (16.4) сходится. Так как lim an = K, то для достаточно
|
|
an |
|
|
|
|
an |
|
|
n→∞ bn |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||
больших n |
|
- K |
< e Þ |
- K < e Þ a |
< (K + e)b |
, è òàê êàê ðÿä |
|||||||||||
|
|
|
|||||||||||||||
|
|
bn |
|
|
|
|
n |
|
n |
|
|
|
|||||
∞ |
|
|
bn |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
å(K + e)bn |
тоже сходится (см. теорему 16.3), то ( см. замечание к тео- |
||||||||||||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
реме 16.5), сходится и ряд (16.1). Эта часть доказательства справедлива |
|||||||||||||||||
è ïðè K = 0 . |
|
|
|
|
|
|
bn |
|
|
1 |
|
||||||
Пусть теперь сходится ряд (16.1). Так как lim |
|
= |
, òî ïî óæå äî- |
||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n→∞ an |
|
K |
||||
казанной первой части теоремы ряд (16.4) тоже сходится. |
|||||||||||||||||
Åñëè æå lim |
an |
= ¥, òî lim |
bn |
= 0, тогда из сходимости ряда (16.1) |
|||||||||||||
|
|||||||||||||||||
|
n→∞ bn |
|
n→∞ an |
|
|
|
|
|
|
||||||||
следует сходимость ряда (16.4), а значит, из расходимости ряда (16.4)
следует расходимость ряда (16.1) (доказательство методом от противного: если бы (16.1) сходился, то по уже доказанному сходился бы и (16.4), что не так). x
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
1 |
|
||
Пример. Исследовать на сходимость ряд å |
2n tg |
. |
||||||||||||||
n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n=1 |
3 |
|
|||
|
|
|
|
|
|
|
|
Ð å ø å í è å |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
æ |
2 |
|
ö |
|
|
|
||
Сравним этот ряд со сходящейся з q = |
|
< 1÷ |
геометрической прогрес- |
|||||||||||||
3 |
||||||||||||||||
∞ |
2 |
n |
|
|
|
|
è |
|
ø |
|
|
|
||||
ñèåé åçæ |
÷ö . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
n=1è 3 |
ø |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
Òàê êàê ïðè n → ∞ бесконечно малая |
tg |
|
эквивалентна бесконечно |
|||||||||||||
3n |
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
1 |
|
2n tg |
|
|
|
||||||||||
малой |
, òî lim |
3n |
= 1Ю по теореме 16.6 исходный ряд сходится. |
|||||||||||||
3n |
|
|
||||||||||||||
|
|
n→∞ |
n |
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3n |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
315 |
|||
6. Ðÿäû
Теорема 16.7 (признак Коши). Пусть дан ряд с неотрицательными
∞
членами åan (16.1) и пусть существует (конечный или бесконечный)
n=1
lim n an = l. Тогда при l < 1 ряд (16.1) сходится, а при l > 1 ряд (16.1) |
||
n→∞ |
|
|
расходится. |
|
|
¡ Пусть l < 1. Возьмем произвольное число q О(l, 1) (ðèñ. 82). |
||
l |
q |
1 |
Ðèñ. 82 |
|
|
Òàê êàê lim n an = l , то $N :"n > N все члены последовательности
n→∞
{n an } попадут в изображенную на рис. 82 окрестность точки l, значит,
∞
"n > N (n an < q ) Þ an < qn . Ðÿä åqn сходится (это геометрическая
n=1
прогрессия со знаменателем q, 0 < q < 1), следовательно (см. замечание к теореме 16.5), ряд (16.1) сходится.
Пусть l > 1; начиная с некоторого номера n an > 1Þ an > 1Þ
lim a ¹ 0 , т.е. ряд (16.1) расходится, так как не выполняется необхо- |
|||||
n→∞ |
n |
|
|
|
|
димый признак сходимости (см. следствие теоремы 16.4). x |
|||||
|
|
|
|
∞ |
1 . |
|
Пример. Исследовать на сходимость ряд åarcsinn |
||||
|
|
|
|
n=1 |
n |
|
|
|
|
Ð å ø å í è å |
|
|
lim n arcsinn 1 |
= lim arcsin 1 = 0 < 1 Ю ряд сходится. |
|
||
|
n→∞ |
n |
n→∞ |
n |
|
Теорема 16.8 (признак Даламбера). Пусть дан ряд с неотрицатель-
∞
ными членами åan (16.1) и пусть существует (конечный или беско-
n=1
нечный) lim an+1 = l. Тогда при l < 1 ряд (16.1) сходится, а при l > 1 ряд
n→∞ an
(16.1) расходится.
¡ Пусть l < 1 . Возьмем такое же произвольное число q О(l, 1) , êàê
при доказательстве теоремы 16.7 (см. рис. 82). Так как lim an+1 = l, òî
n→∞ an
16. Числовые ряды
ìa |
ü |
|
|
|
|
|
ï |
n+1 |
ï |
|
|
|
|
$N :"n > N все члены последовательности í |
|
ý |
попадут в изобра- |
|||
|
||||||
ï |
a |
ï |
|
|
|
|
î |
n |
þ |
æ a |
ö |
|
|
|
|
|
|
|||
женную на чертеже окрестность точки l Ю "n > N |
ç |
n+1 |
< q ÷ |
.  ÷àñò- |
||
|
|
|
ç |
a |
÷ |
|
|
|
|
è |
n |
ø |
|
ности, |
aN +2 |
< q, |
aN +3 |
< q, |
aN +4 |
< q,..., |
aN +n+1 |
< q. Перемножим левые |
|||||||||
|
|
|
|
||||||||||||||
|
aN +1 |
aN +2 |
aN +3 |
|
|
|
aN +n |
|
|
||||||||
и правые части этих неравенств: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
aN +n+1 |
< qn Þ a |
|
|
< a qn. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
aN +1 |
|
|
N +n+1 |
N +1 |
|
|
||||||
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|||||
Íî ðÿä åaN +1qn сходится как геометрическая прогрессия со знамена- |
|||||||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
телем q О(0,1) , тогда по теореме сравнения 16.5 сходится ряд åaN +n+1, |
|||||||||||||||||
а значит, по теореме 16.1 ряд (16.1) сходится. |
|
n=1 |
|||||||||||||||
|
|
||||||||||||||||
Пусть l > 1; начиная с некоторого номера |
|
|
|||||||||||||||
|
|
|
|
an+1 |
> 1Þ a |
> a |
Þ lima |
¹ 0 |
, |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
a |
n+1 |
n |
|
|
n→∞ n |
|
|||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||
следовательно, ряд (16.1) расходится, так как не выполняется н еобходимый признак сходимости (см. следствие теоремы 16.4). x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
n |
|
|
|
|
|
Пример. Исследовать на сходимость ряд å |
n |
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 n! |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Ð å ø å í è å |
|
|
|
|
|
|
|
||||
|
|
nn |
|
|
|
|
(n +1)n+1 |
|
|
a |
|
(n +1)n+1n! |
|
(n +1) n+1 |
|
||||||||
a |
= |
|
|
Þ a |
|
= |
|
|
|
Þ lim |
n+1 |
|
= lim |
|
|
|
|
= lim |
|
|
= |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n |
|
n! |
|
n+1 |
|
(n +1)! |
|
n→∞ an |
n→∞ |
(n +1)! nn |
n→∞ ( n +1) nn |
|
|||||||||||
|
|
|
(n +1)n |
|
|
æ n +1 |
ön |
æ |
|
1 ön (2.7) |
|
|
Þ рядрасходится.. |
||||||||||
= lim |
|
|
|
= lim ç |
|
|
÷ |
= lim ç1+ |
÷ = e |
> 1 |
|||||||||||||
|
|
n |
|
||||||||||||||||||||
|
n→∞ |
|
n |
|
|
n→∞ è n |
ø |
n→∞ è |
n ø |
|
|
|
|
|
|
|
|
||||||
Теорема 16.9(интегральный признак сходимости).Пустьданрядснео-
∞
трицательнымичленами åan (16.1)ипусть an = f (n),гдефункция y= f (x)
n=1
определена,непрерывна,неотрицательнаиневозрастаетприx³1.Тогдаряд (16.1)сходитсяилирасходитсяодновременноснесобственным интегралом
+∞ |
|
ò f (x)dx. |
(16.5) |
1 |
|
316 |
317 |
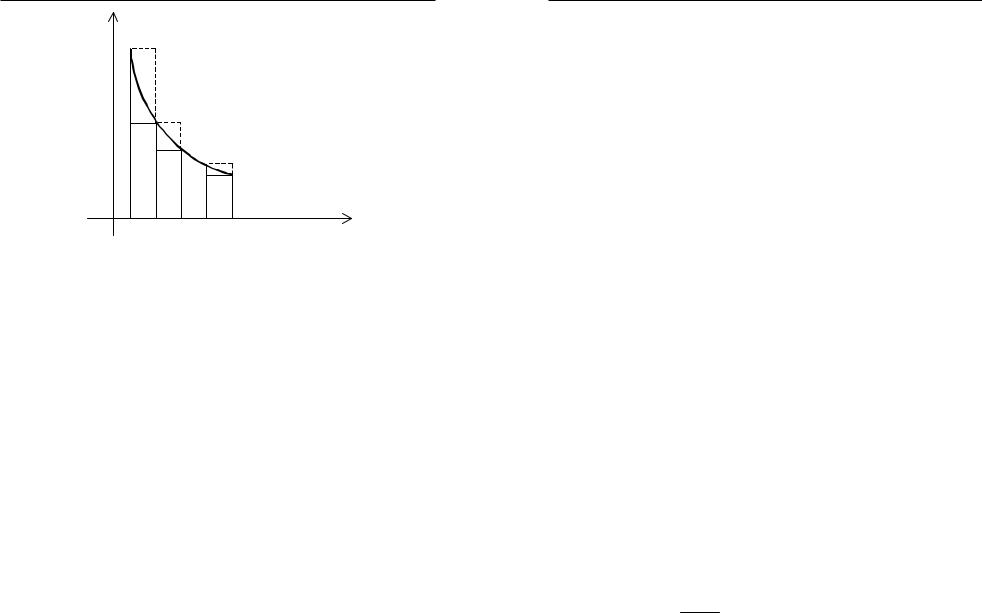
6. Ðÿäû
y
0 1 2 3 ... |
n n+1 |
x |
Ðèñ. 83
¡ Как видно из рис. 83, площадь криволинейной трапеции, т.е.
n+1
ò f (x)dx , заключена между площадями «большой» и «маленькой» сту-
1
пенчатых фигур, которые (как сумма площадей прямоугольников) соответственно равны
1× f (1)+ 1× f (2)+ ...+ 1× f (n) = f (1)+ f (2)+ ...+ f (n) = Sn ;
1× f (2)+ 1× f (3)+ ...+ 1× f (n + 1)= f (2)+ f (3)+ ...+ f (n + 1)= Sn+1 -a1 .
n+1
Таким образом, Sn+1 - a1 £ ò f (x)dx £ Sn.
1
Пусть интеграл (16.5) сходится. Так как f (x) ³ 0, то
|
n+1 |
+∞ |
|
ò f (x)dx £ ò f (x)dx . |
|
Значит, |
1 |
1 |
|
|
|
|
n+1 |
+∞ |
|
Sn+1 £ ò f (x)dx + a1 £ ò f (x)dx + a1, |
|
|
1 |
1 |
16. Числовые ряды
т.е. последовательность {Sn} ограничена сверху, а так как для любого ряда с неотрицательными членами эта последовательность не убывает, то по теореме 2.10 существует конечный lim S , следовательно, ряд (16.1) сходится. n→∞ n
Пусть интеграл (16.5) расходится. Так как f (x) ³ 0, то последо-
|
ìn+1 |
ü |
|
|
|
ï |
ï |
|
|
вательность |
ï ò |
ï |
не убывает. Эта последовательность не |
|
í |
f (x)dxý |
|||
|
î 1 |
þ |
|
n+1 |
может быть ограниченной сверху (если бы |
ò f (x)dx £ M , òî |
|||
c |
|
|
|
1 |
j(c) = ò f (x)dx £ M |
для "c ³ 2, и, аналогично доказательству теоре- |
|||
1
мы сравнения для несобственных интегралов 11.1, интеграл (16.5)
|
|
|
|
|
n+1 |
|
|
|
|
|
|
n+1 |
|
|
|
|
сходится). Тогда lim |
ò |
f (x)dx = +¥ . Íî òàê êàê S |
n |
³ |
ò |
f (x)dx , òî |
||||||||||
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
отсюда и lim S |
n |
= +¥ , а значит, ряд (16.1) расходится. x |
|
|
|
|||||||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
Пример. Исследовать на сходимость ряды å |
|
. Такие ряды называ- |
||||||||||||||
α |
||||||||||||||||
ются рядами Дирихле. |
|
n=1 n |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Ð å ø å í è å |
|
|
|
|
|
|
|
|
|
|
Ïðè a £ 0 lim |
1 |
¹ 0 Ю ряд расходится. При a > 0 функция f (x) = |
1 |
|
||||||||||||
α |
α |
|||||||||||||||
n→∞ n |
|
+∞ |
|
|
|
|
|
|
|
x |
||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||
удовлетворяет всем условиям теоремы 16.6. Но ò |
сходится при a > 1 и |
|||||||||||||||
xα |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
расходится при a £ 1 (см. разд. 11.2), следовательно, ряды Дирихле сходят-
ся при a > 1 и расходятся при a £ 1. В частности, расходится и гармонический ряд
Ряды Дирихле часто берутся в качестве одного из рядов при исследовании рядов на сходимость с использованием теорем 16.5 и 16.6 .
Замечание. Применение к рядам Дирихле признака Даламбера приво-
дит к равенству l = lim nα α = 1, ò.å. ïðè l = 1 ряд (16.1) может сходиться, n→∞ (n + 1)
а может и расходиться. Аналогичный результат справедлив и для признака Коши.
318 |
319 |
