
Методичка_Сигналы
.pdf1
Журкин И.Г., Шавенько Н.К.
СИГНАЛЫ
Учебное пособие по курсу «Автоматизированная обработка аэрокосмической информации»
МОСКВА
2002
2
Министерство щбразования Российской Федерации
Московский государственный университет геодезии и картографии
Журкин И.Г., Шавенько Н К.
СИГНАЛЫ
Учебное пособие по курсу «Автоматизированная обработка аэрокосмической информации»
Для студентов 4 и 5 курсов специальностей «Исследование природных ресурсов» и «Информационные системы в геодезии»
МОСКВА
2002
3
Журкин И.Г., Шавенько Н.К.
Сигналы. Учебное пособие—М.: МИИГАиК, 2002 г., с.
Учебное пособие написано в соответствии с утвержденной программой курса «Автоматизированная обработка аэрокосмической информации», рекомендовано кафедрой вычислительной техники и автоматизированной обработки аэрокосмической информации и утверждено к изданию редакционно-издательской комиссией факультета прикладной космонавтики.
Учебное пособие содержит основные теоретические сведения о сигналах, используемых в процессе автоматизированной обработки информациии и описание двух лабораторных работ, которые апробированы в течение ряда лет в Московском государственном университете геодезии и картографии.
Рецензенты:
4
Гл. 1. Сигналы
§1.1. Основные понятия и классификация
Как отмечалось ранее, сигналы представляют собой физический процесс, несущий информацию или используемый для передачи информации, содержащейся в каком-либо сообщении, то есть сигнал – это форма представления информации на некотором носителе. При этом под носителем понимают некоторые характеристики физических явлений или величины их характеризующие, которые могут меняться как во времени, так и в пространстве.
Если – некоторая характеристика физического явления, информация о котором должна быть передана, то сигнал образуется этой характеристикой как функция
F x, y, z,t |
(1.1) |
где x, y, z – пространственные координаты; t – время.
Функция F определяет структуру сигнала. В зависимости от вида F, все сигналы делятся на детерминированные, для которых функция F выражается функцией, значения которой известны при любых значениях аргументов, и случайные (стохастические), для которых функция F есть случайная функция. В свою очередь детерминированные сигналы подразделяются на периодические и непериодические в зависимости от того, является ли детерминированная функция F периодической или непериодической, а случайные сигналы подразделяются на стационарные и нестационарные.
Стационарный случайный сигнал характеризуется не зависящими от времени статическими характеристиками (закон распределения, математическое ожидание, дисперсия и другие), тогда как у нестационарного случайного сигнала они могут изменяться в каждый фиксированный момент времени.
В зависимости от вида используемых аргументов функции F (пространственные или временные) все сигналы делятся на статические и динамические. Не изменяющиеся во времени сигналы называют статическими, а сигналы, изменяющиеся во времени –
5
динамическими, причем преобразование динамического сигнала в статический называется запоминанием, а обратное преобразование – считыванием.
Интервал возможных значений аргументов функции F называют областью определения сигнала, а диапазон возможного изменения значений функции F называют областью значения сигнала .
Обычно мы имеем дело с элементами сигнала, которые называются значениями сигнала. В зависимости от того, какие значения может принимать сигнал, все сигналы делят на следующие классы:
дискретный дискретного аргумента;
дискретный непрерывного аргумента;
непрерывный дискретного аргумента;
непрерывный непрерывного аргумента.
Первый и последний класс соответственно часто именуется «дискретным сигналом» и «непрерывным сигналом». В качестве аргумента используют либо пространственные координаты (x,y,z), либо время (t), либо (x,y,z,t) – пространствовремя.
Под дискретным сигналом подразумевают любой сигнал, который может принимать только конечное число фиксированных значений.
Дискретность аргумента указывает на то, что значение аргумента определено лишь в конечном числе фиксированных значений из области определения функции F.
Под непрерывным сигналом подразумевают сигнал, значения которого могут принимать любую величину из заданного интервала. Непрерывность аргумента говорит о том, что он может принимать любое значение из области определения.
По методу образования значений все сигналы часто делят на две группы. К первой группе относят сигналы, являющиеся функцией избранной характеристики используемого физического процесса, то есть являющиеся значением самой физической характеристики . Сигналы этой группы в общем случае называют амплитудными сигналами. Они могут быть как непрерывными, так и дискретными. В частности, к сигналам этой группы относят различные аналоговые сигналы и сигналы, получаемые после дискредитации аналогового сигнала по аргументу, по уровню или одновременно по аргументу по уровню.
6
Ко второй группе относят сигналы, которые являются функцией как избранной характеристики используемого физического явления, так и некоторых структурных параметров сигнала (в общем случае это некоторый функционал).
При использовании сигналов для передачи информации необходимо чтобы они обладали двумя видами параметров: информационными и селекции.
Информационными параметрами сигнала называют те его физические параметры, в которых содержится передаваемое сообщение, а параметры селекции служат для возможности выделения данного сигнала из множества подобных.
Все сигналы, относящиеся к первой группе, всегда имеют информативный параметр, а сигналы второй группы делятся на сигналы с информационным параметром
ина сигналы без информационного параметра.
Ксигналам второй группы с информационным параметром относят сигналы, в которых информация содержится в физических характеристиках элемента сигнала. К этой группе, в частности, относят различные импульсные сигналы (амплитудноимпульсные, частотно-импульсные, широтно-импульсные) и частотные сигналы, у которых для передачи сообщения используют изменение частоты, амплитуды или фазы гармонических колебаний.
В сигналах второй группы без информационного параметра информация содержится в комбинации или во взаимном расположении отдельных элементов или значений характеристики физического явления. Чаще всего они строятся на основе каких-либо стандартных импульсов. При этом метод образования этих сигналов из импульсов называется кодированием, причем различают последовательное и параллельное кодирование. При последовательном кодировании значение сигнала состоит из последовательности импульсов (или иных символов), а при параллельном – значение сигнала образуется как совокупность символов, полученных по нескольким каналам. В первом случае для каждого символа выделяется промежуток времени, а во втором – канал связи.
Классификация сигналов представлена на рис.1.1
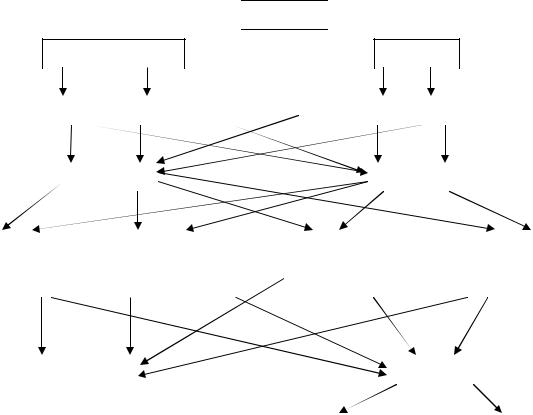
7
 Сигналы
Сигналы 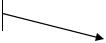
|
Детерминированные |
|
|
|
Случайные |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
Периодические |
|
Непериодические |
|
Стационарные |
|
Нестационарные |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статические |
|
|
|
|
|
Динамические |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретные |
|
Дискретные |
|
Непрерывные |
|
Непрерывные |
дискретного |
|
непрерывного |
|
Дискретного |
|
непрерывного |
аргумента |
|
аргумента |
|
аргумента |
|
аргумента |
|
|
|
|
|
|
|
Первая группа |
|
|
|
Вторая группа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С информационными |
|
|
Без информационных |
|
|
|
параметрами |
|
|
параметров |
|
|
|
|
|
|
|
|
Рис. 1.1
На практике чаще всего приходится иметь дело с одномерными сигналами, которые представляются в виде функции (F) одного аргумента x, y, z или t. И все приведенные выше определения и классификации чаще всего подразумевают именно это.
Однако, наряду с одномерными сигналами, которые можно представить в виде функции одшого аргумента, при автоматической обработке информации (пространственные данные и изображения) приходится иметь дело и с многомерными сигналами, которые могут быть представлены в виде функции нескольких переменных. Так сигналы, соответствующие изображению аэрофотоснимка можно представить в виде функции двух аргументов, в кпчестве которых используются координаты точек снимка x и y. Многомерные сигналы часто называют скалярными полями.
Кроме того при автоматизированой обработке изображений используются сигналы, значение которых могут быть представлены в виде n-мерных векторов. Например, для цветного фотоизображения значение цветовой характеристики каждой
8
точки представляются в виде трехмерного вектора, в качестве компонента которого используется относительные величины основных цветов (при использовании трёхкомпонентных систем представления цвета). Такие сигналы называют многопараметрическими или векторными полями.
Многомерные и многопараметрические сигналы могут быть классифицированы и описаны с помощью тех же понятий, как это было сделано для одномерных сигналов.
§1.2. Модуляция сигналов
Как отмечалось в предыдущем параграфе, для передачи сообщений формируются сигналы, как правило, имеющие два вида параметров: информационные и селекции.
Параметры селекции позволяют выделить полезный сигнал из совокупности сигналов и помех и обеспечивают эффективную передачу информацию по каналам связи. Информационные параметры содержат необходимые сведения о передаваемом сообщении, то есть именно в изменении этих параметров и содержится передаваемое сообщение.
Процесс, при котором информационные параметры, предназначенного для передачи сигнала (сообщения) управляются в соответствии с законом изменения сформированного и непосредственно передаваемого по каналу связи сигнала, будем называть модуляцией. Сформулированный таким образом передаваемый сигнал будем называть модулированным. При этом сигнал, соответствующий закону изменения информационного параметра будем называть модулирующим, сигнал, полученный в результате преобразования – модулированным, а сигнал-переносчик – модулируемым.
Модуляцией называют преобразование одного сигнала, называемого сигналомпереносчиком (носителем), в другой сигнал путём управления информационным параметром сигнала-переносчика в соответствии с законом изменения передаваемого сообщения. Сигнал-переносчик – это материальная основа, представляющая собой некий процесс или объект, который становится носителем информации в процессе модуляции.
Если обозначить сигнал-переносчик через u t , передаваемое сообщение через x t , то при модуляции выполняется преобразование двух сигналов u t и x t в один модулированный сигнал s t , то есть
онепрерывных видах модуляции.
Вслучае использования в качестве сигнала-переносчика периодической последовательности импульсов, говорят об импульсных видах модуляции.
Модуляции, при которых информационный параметр принимает конечное число различных значений, называют дискретными.
Если значения сигнала, полученные при дискретной модуляции, кодируют и передают в виде цифр, то говорят о цифровой модуляции, которая используется при цифровой обработке сигналов.
Классификация различных видов модуляции обычно выполняют исходя из:
вида сигнала-переносчика;
информационного параметра сигнала;
вида передаваемого сигнала или сообщения.
Таблица 1.1. иллюстрирует принятую ГОСТом классификацию различных видов модуляции, исходя из вида сигнала-переносчика u t и вид модулируемого сигнала
x t .
В таблице приняты следующие обозначения для видов модулирующих сигналов
x t :
A – детерминированные непрерывные сигналы;
B – детерминированные дискретные последовательности; C – случайные стационарные неперывные сигналы;
D – случайные стационарные последовательности;
E – случайные нестационарные непрерывные сигналы;
F – случайные нестационарные последовательности;
G – дискретные случайные стационарные последовательности;
H – дискретные случайные нестационарные последовательности.
10
Аналогичные виды сигналов-переносчиков обозначены соответсвенно цифрами
1-8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1. |
||
|
|
|
|
|
|
|
|
|
|
Виды |
|
|
Виды модулирующих сигналов |
|
|
||||
сигналов |
|
|
|
|
|
|
|
|
|
A |
B |
C |
D |
E |
F |
G |
H |
||
переносчиков |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
A1 |
B1 |
C1 |
D1 |
E1 |
F1 |
G1 |
H1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
A2 |
B2 |
C2 |
D2 |
E2 |
F2 |
G2 |
H2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
A3 |
B3 |
C3 |
D3 |
E3 |
F3 |
G3 |
H3 |
|
|
|
|
|
|
|
|
|
|
|
|
: |
: |
: |
: |
: |
: |
: |
: |
|
|
|
|
|
|
|
|
|
|
|
8 |
A8 |
B8 |
C8 |
D8 |
E8 |
F8 |
G8 |
H8 |
|
|
|
|
|
|
|
|
|
|
|
Выбор используемого вида модуляции в основном определяется:
видом модулирующего сигнала или сообщения;
свойством канала;
потенциальной помехустойчивостью;
сложностью технической реализации;
Как было показано в §1, для передачи информации могут использоваться только случайные сигналы и последовательности, так как детерминированный сигнал, значения которого известны, в любой момент времени, не несет никакой информации. Поэтому для передачи сообщений не могут использоваться модулирующие сигналы А и В.
§1.3. Непрерывные и импульсные модуляции
Если в качестве сигнала-переносчика используются детерминированные непрерывные сигналы, у которых под воздействием передаваемого сообщения информационные параметры изменяются непрерывно, то такие виды модуляции называются непрерывными и по привиденной классификации (Таблица 1.1) они относятся к классу 1.
