
Методичка_Сигналы
.pdf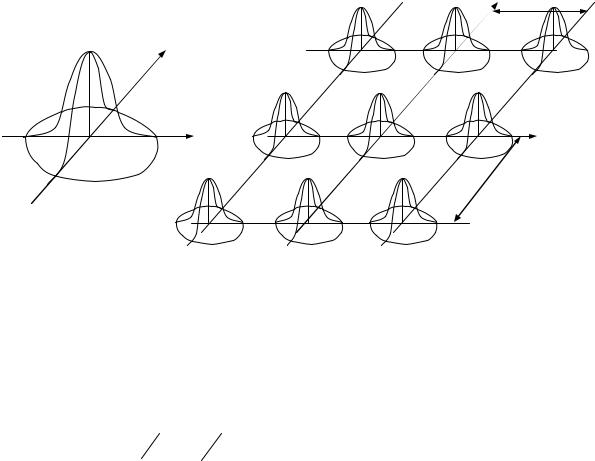
81
2
ωy x
ωy
|
ωx |
|
ωx |
|
2 |
|
y |
a) |
б) |
|
|
|
Рис. 2.18 |
Из рис.2.18 видно, что спектр дискретизированного изображения получается путем бесконечного повторения спектра исходного изображения со сдвигом на
величину, кратную |
2 |
x |
и 2 |
y |
вдоль оси x |
и y соответственно. Если x и y |
|
|
|
|
|
||
выбраны слишком |
большими |
по сравнению |
с шириной спектра FH x , y , то |
|||
соседние спектры будут перекрываться друг с другом, что сделает невозможным восстановление исходного изображения.
Из отсчетов функции Fg x, y можно получить непрерывное изображение путем линейной пространственной интерполяции или с помощью линейной пространственной
фильтрации дискретизированного изображения. Если R x, y |
- импульсный отклик |
интерполирующего фильтра, R x , y - его частотная |
характеристика, то |
восстановленное изображение получается как свертка последовательности отсчетов с импульсным откликом восстанавливающего фильтра:
FB x, y Fg x, y R x, y , |
(2.191) |
где FB x, y - восстановленное изображение.
Подставив значение Fg x, y из равенства (2.190), получим:
82
|
|
FB x, y FH l x, k y R x l x, y k y . |
(2.192) |
l k |
|
Импульсный отклик R x, y выполняет роль двумерной функции, интерполирующей |
|
отсчеты на всю плоскость. Пространственно частотный спектр изображения, восстановленного согласно выражению (2.191), (по свойству свертки) равен произведению частотной характеристики восстанавливающего фильтра на спектр дискретизированного изображения:
|
FB x , y Fg x , y R x , y . |
|
(2.193) |
||||
Подставив выражение для спектра дискретизированного изображения получим: |
|||||||
|
1 |
|
|
|
|
|
|
FB x , y |
R x , y FH x l xs , y |
k ys . |
(2.194) |
||||
x y |
|||||||
|
|
l k |
|
|
|||
Очевидно, что если спектры не перекрываются, а множитель |
R x , y |
||||||
подавляет все сдвинутые |
спектры |
при |
l, k 0 , то спектр |
восстановленного |
|||
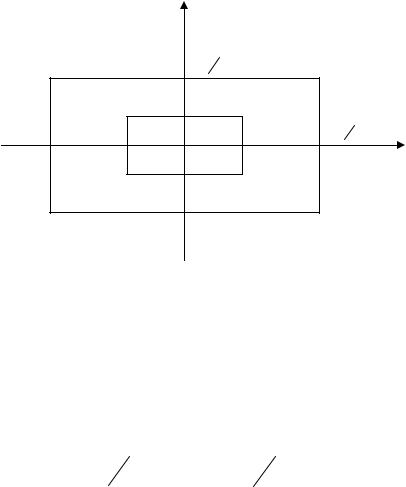
непрерывного изображения будет совпадать со спектром исходного изображения и поэтому изображения также будут одинаковыми. Для изображений с ограниченной шириной спектра x x.max .u и y y.max .u первое условие выполняется, если интервал дискретизации выбран так, что прямоугольная область, ограниченная
верхними граничными частотами спектра (рис.2.19) лежит |
внутри прямоугольной |
||||||
|
|
|
|
|
ys |
|
|
|
|
xs |
, |
|
|
|
|
|
|
|
|
|
|||
области, определяемой половинами частот дискретизации |
2 |
2 |
. |
||||
|
|
|
|||||
83
y
ys 2
y.max.u.
|
x.max.u. |
xs |
2 |
|
|
||
|
|
|
x
Рис. 2.19
То есть выполняются неравенства
x.max .u |
xs |
, |
y.max .u |
ys |
(2.195) |
|||
2 |
2 |
|
||||||
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
x |
|
, |
|
y |
|
. |
(2.196) |
|
|
x.max .u |
|
|
y.max .u |
|
|||
Это значит, что шаг дискретизации не должен превышать половины периода пространственной гармоники, соответствующей самым мелким деталям изображения. Это условие эквивалентно теореме Котельникова о дискретизации одномерных сигналов. В этом случае, когда отсутствует наложение спектров, исходное изображение можно абсолютно точно восстановить путем пространственной фильтрации с помощью соответствующего фильтра.
В реальных системах дискретизации изображений дискретизирующая решетка имеет конечные размеры, ширина дискретизирующих импульсов заметно отличается от нуля, а отсчеты изображения могут быть взяты с недостаточной частотой. Кроме этого, искажения могут вноситься оптической системой и сканирующей диафрагмой.
Рассмотрим влияние некоторых из этих факторов.
1. Если спектр изображения ограничен по ширине, а x и y удовлетворяет теореме Котельникова, то конечная ширина импульса дискретизации приводит к тем же результатам, как если бы исходное изображение перед идеальной дискретизацией подверглось линейному искажению (смазыванию). Однако конечность размеров

84
дискретизирующего импульса не всегда является недостатком. В случае, если спектр исходного изображения очень широкий и оно дискретизируется с недостаточной частотой, то импульс с конечными размерами фактически осуществляет низкочастотную фильтрацию исходного изображения, что приводит к сужению спектра и, следовательно, уменьшает ошибки, вызванные наложением спектров.
2. Если отсчеты изображения взяты с недостаточной частотой, то имеет место наложение спектров, что ведет к тому, что в восстановленном изображении будут внесены ложные пространственные гармоники. (В оптике это явление называют муарэффектом).
Действительно из (2.190) видно, что спектр дискретизированного изображения можно представить в виде
F |
|
|
, |
|
|
1 |
F |
|
|
, |
|
F |
|
|
, |
|
, |
(2.197) |
|
|
x y |
|
|
|
|
||||||||||||
g |
|
x |
|
y |
|
H |
|
x |
|
y |
Q |
|
x |
|
y |
|
|
|
где FH x , y - описывает спектр исходного изображения, |
дискретизированного с |
|||||||||||||||||
периодом x , y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а слагаемое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l xs , y k ys |
|
|||||||
FQ x , y FH x |
(2.198) |
|||||||||||||||||
l k l 0,k 0
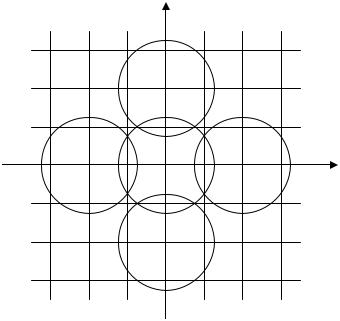
описывает те компоненты спектра дискретизированного изображения, которые получаются при повторении исходного спектра с периодами xs 2 x и ys 2 y .
На рис.2.20 изображен спектр двумерной функции, дискретизированной с недостаточной частотой.
85
y
ys
12 ys
x
12 ys
ys
xs 1 |
|
1 |
|
2 |
xs |
2 xs |
xs |
|
Рис. 2.20
При отсутствии наложения спектров оптимальную интерполяцию отсчетов изображения можно получить, пропуская дискретизированное изображение через идеальный фильтр нижних частот.
§2.20. Дискретное преобразование Фурье
Как известно, при цифровой обработке сигнала непрерывные сигналы представляются в дискретной форме: в виде закодированных отдельных отсчетов. Рассмотренные выше методы частотного анализа использовались лишь для непрерывных сигналов, однако и при цифровой обработке широко используется частное представление сигналов, то есть перевод их из временной или пространственной области в область частот. Для этого применяется дискретное преобразование Фурье (ДПФ), во многом аналогичное преобразованию Фурье, используемому для частотного анализа непрерывных сигналов.
Дискретное преобразование Фурье (ДПФ) определяет линейчатый спектр дискретизированной периодической функции времени или координаты. Обратное дискретное преобразование Фурье позволяет восстановить функцию времени по ее

86
спектру. ДПФ служит для анализа периодических функций и алгоритм этого
преобразования можно получить исходя из рядов Фурье. |
|
|||||
|
Пусть |
x t непрерывная периодическая функция с периодом |
T и частотой |
|||
f 1 |
T |
; 2 f 2 |
T |
так что |
|
|
|
|
|
|
|
||
|
|
|
|
|
x t x t mT , |
(2.199) |
где m - целое число.
Тогда функцию x t можно разложить в ряд Фурье:
x t |
|
|
|
|
|
|
Cn e jn t , |
0 t T , |
(2.200) |
||||
|
n |
|
|
|
|
|
где коэффициенты разложения Cn определяются из соотношения |
|
|||||
|
|
T |
0 |
|
|
|
|
Cn |
1 |
T |
x t e jn t dt . |
(2.201) |
|
|
|
|
||||
Cn - комплексная величина и из нее можно определить амплитуду и фазу гармоник. Из теории квантования известно, что однозначная дискретизация функции
возможна лишь тогда, когда ее спектр ограничен, то есть |
|
|||||||||
Cn 0 , |
|
при |
|
n |
|
n1 , |
(2.202) |
|||
|
|
|
||||||||
где n1 - значение n, задающее частоту f1 : |
|
|
|
|
|
|
|
|
||
f |
1 |
n |
f |
n1 |
. |
(2.203) |
||||
|
||||||||||
|
1 |
|
T |
|
||||||
|
|
|
|
|
||||||
В соответствии с теоремой Котельникова интервал дискретизации (расстояние между отсчетами) T равен
T |
1 |
|
|
1 |
|
T |
, |
(2.204) |
|
2 f |
1 |
2n f |
2n |
||||||
|
|
|
|
|
|||||
|
|
|
1 |
|
1 |
|
|
так что число отсчетов на период T будет N:
(2.205)
В результате дискретизации получим периодическую функцию, которую нормализуем относительно T :
|
|
t |
N 1 |
|
t |
t |
|
|
|||
x |
|
|
|
x |
|
|
|
|
k . |
(2.206) |
|
|
|
T |
|||||||||
|
T |
k 0 |
|
T |
|
|
|
||||
Эта функция определена на интервале |
|
|
|
|
0 t T |
или 0 |
t |
N . |
|
T |
||||
|
|
|

87
Применим к этой функции преобразование Фурье, тогда
|
|
|
|
|
|
1 |
N 1 |
|
|
|
t |
|
|
2 j n |
|
t |
|
|
t |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Cn |
|
|
|
x |
|
|
|
|
|
|
|
|
|
e N |
T d |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
T |
|
|
|
|
|
|
T |
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
N 1 |
N 1 |
|
|
|
|
t |
|
|
|
t |
|
|
|
|
|
|
2 j n |
|
t |
|
t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
k |
e |
N |
|
T d |
|
, |
|||||||||||
|
|
N |
|
|
|
|
|
|
T |
|
|
|
||||||||||||||||||||||||
|
|
|
0 |
k 0 |
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
T |
|||||||||||||||||
так как 2 |
T |
, а T T N . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поменяем знак суммы и интеграл местами и с учетом того, что |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
|
|
t |
|
x k |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
k d |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
T |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
N 1 |
|
|
2 j kn |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Cn |
|
|
x k e N . |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где N - общее число отсчетов;
x k - отдельные отсчеты 0,1,2,..., N 1 ; n - номер гармоники.
Обратное дискретное преобразование Фурье, соответственно, имеет вид:
N 1 2 j kn
x k Cn e N .
n 0
(2.207)
(2.208)
(2.209)
(2.210)
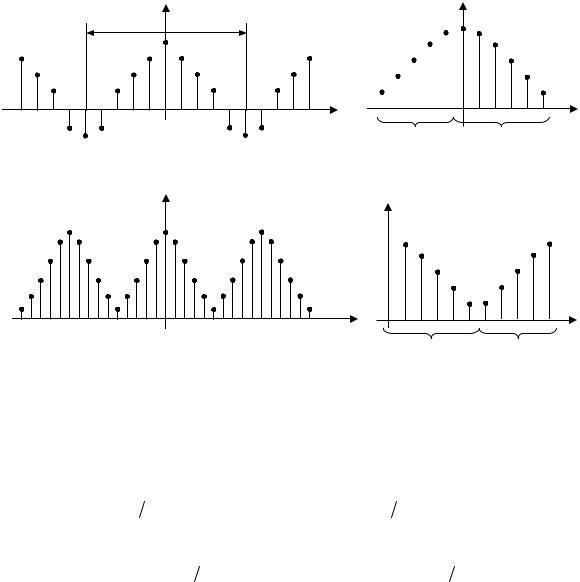
Тот факт, что спектр является периодическим, вытекает из периодичности любой дискретизированной функции, а дискретный характер спектра связан с тем, что сама дискретизируемая функция периодична. Выборки x k непрерывной функции x t и ее спектр X n после дискретизации представлены на рис.2.21.
88
|
|
x(k) |
|
|
|
Xн(n) |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
-6 |
-5-4 |
|
4 5 6 |
|
|
|
-9 -8 -7 |
-3 -2 -1 |
1 2 3 |
7 8 9 |
k |
|
n |
|
|
a) |
|
II |
в) |
I |
|
|
|
|
|
X(n) |
Cn |
|
-15 |
-10 |
-5 |
0 |
5 |
10 |
15 n |
|
|
n |
|
|
|
б) |
|
|
|
I |
г) |
II |
|
|
|
|
|
|
|
|
|
Рис. 2.21
Спектр, получаемый в результате ДПФ можно интерпретировать следующим
образом. Первые N |
2 1 точек Cn соответствуют N 2 1 спектральным линиям |
|||||||
спектра непрерывной |
функции x t на положительных |
частотах, как показано |
на |
|||||
рис.2.21в,г, а последние N |
2 1 точек |
Cn соответствуют N |
2 1 |
спектральным |
||||
линиям на отрицательных частотах. |
|
|
|
|
|
|||
Вычисление дискретного преобразования Фурье производится по алгоритму |
|
|||||||
|
|
|
1 |
N 1 |
|
|
|
|
|
|
Cn |
x k W nk , |
|
|
(2.211) |
||
|
|
|
|
|
||||
|
|
|
N k 0 |
|
|
|
|
|
2 j |
|
|
|
|
|
|
|
|
где W e N . |
|
|
|
|
|
|
|
|
Нетрудно получить |
схему |
вычислений, |
позволяющую |
найти |
N |
значений |
Cn |
|
(дискретного спектра) по N значениям отсчетов x k . Пример такого алгоритма представлен на рис.2.22.
89
Представленный алгоритм очевиден, но он не оптимален, так как требует много вычислений.
Алгоритмы ДПФ, позволяющие достигнуть сокращения вычислительной нагрузки, известны под общим названием «быстрое преобразование Фурье». Следует подчеркнуть, что это не новое преобразование, а всего лишь способ выполнения ДПФ.
90
Лабораторные работы.
Лабораторная работа № 1.
Модуляция сообщений.
Описание лабораторной работы выполнено с использованием программного продукта Mathcad.
1.Промоделировать процесс модуляции непрерывного сообщения непрерывными видами модуляций (амплитудной, частотной, фазовой).
Вкачестве исходного непрерывного сообщения взять сигнал x(t)=0.05+k·t, длительностью T=1/k (сек.), где k-номер по списку.
Вкачестве сигнала переносчика взять гармонический сигнал U(t)=B·cos(10·k·t+φ), где B-взять из таблицы, k-номер по списку, φ=const.
Для этого выполнить:
а) Построить графики сигналов U(t) и x(t);
б) Построить на одном экране графики сигналов x(t) и Sa(t)-промодулированный по амплитуде сигнал U(t):
Sa(t)=B[x(t)]·cos(10·k·t+φ)=B·x(t)·cos(10·k·t+φ).
в) Построить на одном экране графики сигналов x(t) и Sч(t)-промодулированный по частоте сигнал U(t):
Sч(t)=B·{cos[10·k·x(t)·t+φ)=B·cos{10·k·[1+1.5·x(t)]·t+φ}.
г) Построить на одном экране графики сигналов x(t), U(t) и Sф(t)- промодулированный по фазе сигнал U(t):
Sф(t)=B·cos[10·k·t+φ·(x(t))]=B·cos[10·k·t+φ0·x(t)], где φ0 при любом t из области задания должно подчиняться условию: φ0·xmax(t)<2·π.
Промоделировать процесс модуляции непрерывного сообщения импульсными видами модуляции (амплитудно-импульсной, частотно-импульсной и широтноимпульсной)
Вкачестве исходного непрерывного сообщения взять сигнал x(t)=0.05+k·t длительностью T=1/k.
Вкачестве сигнала переносчика взять последовательность стандартных импульсов
длительностью T=1/k. Амплитуда импульсов равна 1, период следования Tи=0.1·T, скважность равна 0.2.
Для этого выполнить:
а). Построить график последовательности импульсов,задав ее следующим образом:
t:=0,1/100·k |
T=1/k |
n:=0,1..20 |
n-номер импульса; |
Y1(n,t):=if(n·Tи+∆t >t, 1, 0) |
Tи=0.1·T=0.1/k; |
Y2(n,t):=if(n·Tи >t, 1, 0) |
∆t-длительность импульса; |
Y(n,t):=Y1(n,t)-Y2(n,t) |
∆t=0.2·Tи=0.02/k; |
Y(t):=Σ Y(n,t) |
-последоват. импульсов. |
б). Построить графики исходного сообщения x(t) и модулированной по амплитуде последовательности импульсов Ya(t).
Для этого в программе задания последовательности импульсов заменить постоянную амплитуду импульсов (равную 1 ) на переменную-x(t), но в этом случае
вершины импульсов не будут плоскими, гораздо лучше произвести замену на x(n Tи ). в). Построить графики исходного сообщения x(t) и модулированной по частоте
последовательности импульсов Yч(t).
