Методичка_Сигналы

71

Обозначив GT Ck и повторив процедуру предельного перехода при T для

формулы (2.143), можно получить каноническое разложение стационарной случайной функции X t :

где функция Sx есть дисперсия случайной функции G d .

Отметим основные свойства функции спектральной плотности. Для этого воспользуемся формулой Эйлера и перейдем от формулы (2.150) к одностороннему спектру в тригонометрической форме представления:

откуда видно, что функция Sx является действительной и четной функцией, то есть

Sx Sx .

Поэтому в выражении (2.149) тоже можно ограничиться только положительными частотами:

Выражения (2.149) и (2.150), а также (2.154) и (2.155) являются парами интегрального преобразования Фурье (прямые и обратные). Исходя из свойств преобразования Фурье корреляционная функция Kx и спектральная плотность

Sx подчиняются закономерности: чем уже одна из них, тем протяженнее вторая, и наоборот.

Интересно отметить, что площадь, ограниченная непрерывной кривой Sx на спектральной диаграмме, равняется дисперсии Dx случайной функции X t .

Действительно, положив в формуле (2.155) 0 , получим:

72

рассматривать как среднюю мощность, выделяемую этим напряжением на активном сопротивлении 1 Ом:

Dx М X 2 t Px .

Следовательно, величина

dPx Sx d

представляет собой долю средней мощности, выделяемой составляющими спектра,

§2.18. Случайные поля при исследовании природных образований

Распределение яркостей, соответствующее некоторому участку земной поверхности или облакам в атмосфере, как и распределение высот рельефа, в общем случае можно рассматривать как случайную функцию двух переменных, то есть как случайное поле.

Если для случайной функции вводилось понятие стационарности, то для случайных полей вводится понятие однородности. Для однородного случайного поля математическое ожидание является постоянной величиной, а корреляционная функция зависит только от вектора, определяемого разностью координат двух точек. В двумерном однородном случайном поле с помощью двумерного преобразования Фурье по известной корреляционной функции Kx 1, 2 можно найти двумерную спектральную плотность Sx 1 , 2 :

Sx 1, 2 найти корреляционную функцию Kx 1 , 2 .

73

Если на плоскости, на которой задано однородное случайное поле, зафиксировать прямую линию, то в сечении поля на этой прямой получается стационарная случайная функция. В сечениях однородного случайного поля по прямым, имеющим различное направление, получаются стационарные случайные функции с одинаковым математическим ожиданием, но, вообще говоря, с различными дисперсиями и корреляционными функциями.

Частным случаем однородного случайного поля является однородное изотропное случайное поле. Для однородного изотропного случайного поля корреляционная функция не зависит от направления, а зависит только от расстояния между двумя точками. В сечениях такого поля по прямым линиям получаются стационарные случайные функции с одинаковыми характеристиками. Случайные поля, которые не являются изотропными, называют анизотропными.

Экспериментальные исследования распределения яркостей аэроландшафтов показывают, что условию однородности сравнительно хорошо удовлетворяют молодые леса, свежие вырубки, луга с однородной растительностью, пашни с однородными почвами, а также водная поверхность. В то же время старые леса, старые вырубки, луга с разнородной растительностью и пашни с разнородными почвами, а также населенные пункты плохо соответствуют условию однородности.

Анизотропный характер природных образований четко проявляется в том случае, когда существенный вклад в распределение яркости вносят объекты, отбрасывающие тень. Наиболее отчетливо анизотропность природных образований проявляется при малых высотах Солнца. Кроме того, анизотропный характер ландшафта может быть связан с ветровыми, а также антропогенными воздействиями.

Для некоторых видов лугов и болот случайное поле яркостей можно считать однородным и изотропным.

Исследование профилей изображений лесных массивов показывает, что соответствующие спектральные плотности обычно имеют максимум при частотах около 0,1 м-1 .

Экспериментальные исследования статистической структуры изображений облачности приводят к выводу, что эти изображения обычно не удовлетворяют условиям однородности, но среди них можно выделить изображения мелких групп облаков, которые удовлетворяют этому условию.

74

С целью повышения достоверности распознавания природных образований предполагается наряду с многоспектральной съемкой осуществлять на борту носителя съемочной аппаратуры пространственную фильтрацию исследуемого поля яркостей. Пространственную фильтрацию предполагается производить таким образом, чтобы можно было определять спектральную плотность, характеризующую статистическую структуру исследуемого участка местности. Для этой цели удобно использовать оптические устройства в сочетании с голографией.

Если метод многоспектральной съемки часто называют спектрометрическим, так как он основывается на измерении собственного и отраженного излучения природных образований в различных диапазонах спектра, то метод, основанный на измерении характеристик радиации, отображающих статистическую структуру исследуемых объектов, называют структурометрическим. Спектрометрический метод позволяет получить среднее значение яркости внутри каждого элемента разрешения исследуемого участка местности для различных диапазонов спектра электромагнитного излучения. Однако величина элемента разрешения при этом ограничивается возможностями канала передачи информации. Поскольку при использовании структурометрического метода передается не само изображение, а только некоторые его характеристики, то при этом может быть передана информация о пространственном распределении элементов, значительно меньших размеров. Эта информация может быть использована в качестве дополнительного опознавательного признака исследуемых объектов.

§2.19. Математическое описание непрерывных двумерных сигналов на примере изображений

Распределение энергии источника светового излучения по пространственным координатам x, y времени t и длинам волн можно описать функцией

75

Таким образом, функция C x, y, t, является ограниченной функцией четырех ограниченных переменных.

Ощущение светлоты, возникающее в зрительной системе человека, обычно определяется мгновенной яркостью светового поля, то есть величиной

где Vs - спектральная чувствительность человеческого зрения.

В технических устройствах вводят аналогичную функцию, которая описывает изображение для i-й спектральной зоны:

где Si - спектральная чувствительность i-того датчика.

Функция F x, y, t представляет собой распределение яркости или какой-либо другой физической величины, связанной с яркостью. Очень часто, особенно при работе с изображениями, аргумент t меняется дискретно, поэтому в дальнейшем аргумент t можно опустить.

При моделировании систем обработки двумерных сигналов вводится понятие двумерной линейной системы. Система называется линейной, если к ней применим принцип суперпозиции, то есть

плоскости x, y .

Если на входе линейной системы действует сигнал F x, y , то на выходе имеет место сигнал

76

Можно поменять местами операции линейного преобразования и интегрирования, так как линейный оператор действует только на тот множитель подинтегрального выражения, который зависит от пространственных переменных x, y .

Запишем второй множитель подинтегрального выражения в виде

и будем называть эту функцию импульсным откликом двумерной системы. Подстановка H x, y, , в соотношение (2.164) дает интеграл суперпозиции

Линейная двумерная система называется пространственно-инвариантной, если ее

77

3. Спектр функции, полученной в результате перемножения двух функций F x, y и H x, y , пропорционален свертке спектров исходных функций, то есть

где F x , y QF F x, y - спектр функции; H x , y QF H x, y - спектр функции.

Наряду с одномерными сигналами, которые рассмотрены ранее, при моделировании различных полей, например, изображениями, приходится иметь дело с двумерными сигналами. К таким сигналам также может быть применено преобразование Фурье, которое в этом случае носит название двумерного. В результате двумерного преобразования Фурье сигнал F x, y , описывающий, скажем, изображение, преобразуется в двумерный спектр (двумерную спектральную плотность) G x , y этого изображения, который определяется из соотношения

По известному Фурье-спектру может быть восстановлено исходное изображение

F x, y :

78

3. Изменение масштаба пространственных переменных приводит к обратному изменению масштаба пространственных частот и пропорциональному изменению значений спектра

Наоборот, сдвиг на частотной плоскости вызывает фазовые изменения исходной функции

При цифровой обработке изображений их обычно представляют в виде массива чисел, полученных в результате дискретизации исходного изображения по пространственным переменным. После обработки получают новые числовые массивы, используемые для восстановления изображений, используемых человеком. Отсчеты изображения получают в результате измерения некоторых физических характеристик реального изображения. При дискретизации и восстановлении непрерывных изображений обрабатываемые изображения обычно рассматривают как детерминированные поля.

Пусть функция FH x, y описывает непрерывное изображение, представляющее собой распределение яркости, оптической плотности или какого-либо другого

79

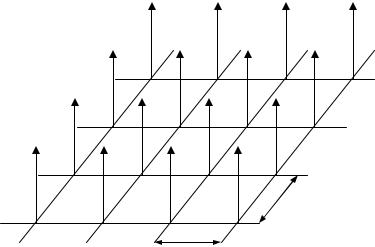
параметра изображения. В идеальной системе дискретизации изображений пространственные отсчеты исходного изображения получаются путем перемножения функции FH x, y с пространственно-дискретизирующей функцией

l k

состоящей из бесконечного числа дельта-функций, заданных в узлах решетки с шагом

x, y (рис.2.17).

∆y

∆x

Рис. 2.17

Тогда дискретизированное изображение описывается выражением

Fg x, y FH x, y S x, y FH l x, k y x l x, y k y , (2.185)

lk

вкотором учитывается, что функцию FH x, y можно внести под знак суммирования и

задать ее значения только в точках отсчета.

Для анализа процесса дискретизации удобно использовать спектр Fg x , y ,

получаемый в результате непрерывного двумерного преобразования Фурье дискретизированного изображения