
Методичка_Сигналы
.pdf
41
B S t sin tdt - мнимая часть S i ;
S A 2 B 2 - модуль S i или спектр непериодического сигнала;
arctg |
B |
- фаза |
|
|
i . |
|
|
|
|
|
|
||||||||||
S |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как A - четная функция частоты, а B - нечетная относительно частоты |
|||||||||||||||||||||
, то, как и в случае ряда Фурье, модуль |
спектральной плотности S |
- есть |
|||||||||||||||||||
функция четная, а фаза |
- нечетная относительно частоты. |
|
|||||||||||||||||||
Обратное преобразование Фурье так же легко привести к тригонометрической |
|||||||||||||||||||||
форме. Действительно в соответствии с (2.30) и учетом (2.43) имеем: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
U t |
|
|
|
i ei t d |
S ei t d |
|
|||||||||||||
|
|
|
S |
|
|||||||||||||||||
|
|
2 |
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.47) |
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
S |
|
cos t d |
|
|
S sin t d . |
|
||||||||||||
|
|
|
2 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Второе слагаемое из-за нечетности подинтегрального выражения равно нулю, |
|||||||||||||||||||||
следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
U t |
|
|
|
S cos t d |
|
S cos t d . |
(2.48) |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||
Преимуществом тригонометрической формы записи преобразования Фурье является его более простое и удобное физическое толкование.
§2.7. Основные свойства преобразования Фурье
1.Свойство линейности.
Если S1 - спектральная плотность сигнала s1 t , а S2 - сигнала s2 t , то при любых произвольных постоянных a1 и a2 спектральная плотность сигнала
S t a1s1 t a2 s2 t
будет равна |
|
S a1S1 a2 S2 , |
(2.49) |
что следует из линейности операции интегрирования. 2.Свойство симметрии.
42
Если сигнал s t имеет спектральную плотность S , то спектральная плотность сигнала S t будет 2 s .
Действительно, как следует из (2.39) при t t
|
|
|
2 s t |
S e i t d . |
(2.50) |
Приведем в этом равенстве последовательно ряд замен переменных:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 s t S e i x t dx ; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 s S x e i x dx ; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 S S t e i t dt S S t . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, спектральная плотность сигнала S t |
равна 2 s . Если s t |
||||||||||||
- четная функция, то s s |
и |
|
спектральная |
плотность |
сигнала |
S t равна |
|||||||
2 s . |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Свойство изменения масштаба. |
|
|
|
|
|
|
|
|
|
||||
Если сигнал s t имеет спектральную плотность |
S , |
то при |
изменении |
||||||||||
масштаба исходного сигнала, то есть для сигнала s a t |
( a -любая действительная |
||||||||||||
постоянная) спектральная плотность равна |
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
S |
. |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Действительно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
S s a t |
|
|
|
|
|
|
|
|
|
||||
|
s a t e i t dt . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведем замену переменных a t x , тогда |
|
|
|
|
|
|
|||||||
а) при a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
S s at |
|
|
|
|
|
S |
|
|
|
|
|||
1 |
s x e i a x dx 1 |
; |
|
(2.51) |
|||||||||
|
a |
|
|
|
a |
a |
|
|
|
|
|||
б) при a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
S s at |
1 |
|
|
|
|
1 |
S |
|
. |
|
|
||
s x e i a x dx |
|
(2.52) |
|||||||||||
|
a |
|
|
|
|
a |
a |
|
|
|
|||
43 |
|
|
|
|
|
|
s a t равна |
|
1 |
|
|
Следовательно, спектральная плотность сигнала |
|
|
S |
. |
|
|
a |
||||
|
|
|
a |
||
4. Свойство частотного сдвига. Если S спектральная плотность сигнала s t ,
то сигналу |
s t ei 0t |
соответствует |
спектральная плотность S 0 , |
то есть |
||||||
умножение сигнала s t |
на ei 0t сдвигает весь спектр S на частоту 0 . |
|
||||||||
Для доказательства этого свойства применим обратное преобразование Фурье к |
||||||||||
спектру S 0 и произведем замену переменных 0 x , тогда |
|
|||||||||
|
|
1 |
S 0 ei 0t d |
1 |
S x ei x t ei x0 t dx s t ei 0 t . |
(2.53) |
||||
|
|
|
2 |
|||||||
|
|
2 |
|
|
|
|
|
|
||
Таким |
образом, |
сигналу s t ei 0t |
соответствует |
спектральная плотность |
||||||
S 0 . |
|
|
|
|
|
|
|
|
|
|
5. Свойство временного сдвига. |
|
|
|
|
|
|
||||
Если S( ) есть |
спектральная |
плотность |
сигнала |
s t , то сигналу |
s t t0 |
|||||
соответствует спектральная плотность |
S e i t0 |
. Для доказательства этого свойства |
||||||||
применим прямое преобразование Фурье к сигналу s t t0 |
и сделаем в нем замену |
||||||||||||||||||
переменных t t0 x , тогда |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
s t t0 e i t dt |
s(x) e i x t0 dt e i t0 s(x) e i xdx S( ) e i t0 . (2.54) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким |
образом, |
сигналу |
s t t0 соответствует |
спектральная плотность |
|||||||||||||||
S e i t0 |
. Другими словами, при сдвиге сигнала на t0 , его амплитудный спектр не |
||||||||||||||||||
меняется, а изменяется только фазовый спектр на величину - t0 . |
|
||||||||||||||||||
6. Если сигнал s1 t имеет спектральную плотность S1 , а сигнал s2 t S2 , |
|||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
||
s1 |
t s2 t |
dt |
s1 t dt S2 ei t d |
|
|
S2 d s1 |
t ei t dt |
||||||||||||
2 |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2.55) |
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
S2 |
S1 d |
|
|
S2 S1 |
d , |
|
|
|||||||||
2 |
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где S |
– комплексно сопряженная с S функция. |
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
44
7. Если сигнал s t со спектральной плотностью S проходит через некоторое звено с предаточной функцией W p , то спектральная плотность выходного сигнала
S' равна |
|
S' S W i . |
(2.56) |
§2.8. Распределение энергии в спектре непериодического сигнала
Если задан непериодический сигнал s t , физическим представлением которого может быть электрическое напряжение на активном сопротивлении в 1 Ом, то можно найти количество энергии, выделяемое на этом сопротивлении за время действия сигнала:
|
t dt . |
|
E s2 |
(2.57) |
Понятие энергии сигнала имеет смысл только в том случае, если интеграл (2.57) конечен.
Сигналы с конечной энергией называют энергетическими. Если сигналу s t соответствует спектральная плотность S , то используя обратное преобразование Фурье и, меняя порядок интегрирования, можно записать:
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
i t |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
E s |
|
|
t dt |
s t s t dt s t |
|
|
|
|
|
S e |
|
d dt |
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.58) |
|||||||||||||||||||
|
|
|
1 |
|
|
s t |
ei t dt d |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
d . |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
S |
S |
S |
|
||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Для действительной функции s t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
где |
|
- комплексно-сопряженна |
|
|
функция, и поэтому |
|
|
||||||||||||||||||||||||||||||||||||||||||||
S |
S |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
причем, как указывалось ранее (§2.4), |
|
S |
|
|
2 - четная функция. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
E s2 t dt |
|
|
S |
|
2 d |
|
|
|
|
|
S |
|
2 d . |
|
(2.59) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||

|
|
|
|
45 |
|
S |
|
2 - называют спектром плотности энергии или спектральной плотностью энергии |
|
|
|
|||
сигнала, физический |
смысл которого - энергия, приходящаяся на единицу полосы |
|||
частот при текущей |
частоте ω (размерность: энергия герц). Соотношение (2.59), |
|||
известное как равенство Парсеваля, показывает, что энергию, выделяемую непериодическим сигналом за время его действия, можно найти, интегрируя квадрат модуля его спектральной характеристики во всем интервале частот.
В отличие от формулы (2.33) формула (2.59) определяет не среднюю мощность, которая для любого непериодического абсолютно интегрируемого сигнала равна 0 (так как T ), а полную энергию, выделяемую сигналом s t за все время его действия.
Спектральная плотность энергии, характеризующая распределение энергии по спектру сигнала, существует лишь для энергетически ограниченных сигналов (для которых выражение (2.57) конечно), к которым применимо преобразование Фурье. Если же значение интеграла (2.57) бесконечно, то понятие энергии сигнала теряет смысл. В этом случае рассматривают среднюю мощность сигнала. Сигналы с
ограниченной мощностью называют мощностными. |
|
|||||||||||||||||||
Определим среднюю мощность непериодического сигнала |
s t как среднюю |
|||||||||||||||||||
мощность W, рассеиваемую на активном сопротивлении величиной 1 Ом в течение времени |
||||||||||||||||||||
(Т) действиясигнала, тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
T 2 |
t dt . |
|
||||||||||||
|
|
W lim |
|
T |
s2 |
(2.60) |
||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
T T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Непериодическийсигнал s t представимконечнымповременисигналом sT t : |
||||||||||||||||||||
|
|
|
s t , при |
|
t |
|
T ; |
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sT |
t |
|
|
|
|
|
|
|
|
|
2 |
|
|
(2.61) |
|||||
|
|
|
0, при |
|
t |
|
|
|
T . |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||
При конечном Т сигнал s t |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
имеет конечную энергию, и тогда, в соответствии (2.59), |
||||||||||||||||||||
энергия ET |
сигнала sT t определится из выражения: |
|
||||||||||||||||||
|
T 2 |
1 |
|
|
|
|
|
|
||||||||||||
|
ET |
s2 t dt |
|
|
|
|
|
|
ST |
|
2 d , |
(2.62) |
||||||||
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|||||||||||||||||||
|
T |
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ST |
- спектральная плотность сигнала s t . Следовательно, |
|
||||||||||||||||||

46
|
E |
|
|
1 |
|
T 2 |
|
|
|
|
|
|
1 |
|
|
|
|
ST |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
W lim |
T |
lim |
|
|
|
|
s2 t dt |
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
d . |
(2.63) |
||||||||
|
T |
|
T |
|
2 |
|
|
T |
|||||||||||||||||||||||
T |
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если предел под знаком интеграла существует, то эта функция называется |
|||||||||||||||||||||||||||||||
спектральнойплотностьюмощности P , то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
P |
lim |
|
S |
T |
|
|
2 |
. |
|
|
|
|
|
|
(2.64) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно доказать, |
что |
|
P 2 |
|
|
|
|
|
|
2 n 0 и среднюю |
мощность |
||||||||||||||||||||
|
Cn |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сигнала W, с учетом четностифункции P , можнопредставитьввиде: |
|
||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
W |
|
|
|
P d |
|
P d . |
|
|
|
|
(2.65) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
§2.9. Корреляционныефункциидетерминированныхсигналов
С физической точки зрения корреляционная функция характеризует взаимосвязь или взаимозависимость двух мгновенных значений одного или двух различных сигналов в моменты времени t1 и t2 t1 . В первом случае корреляционную функцию часто называют автокорреляционной, а во втором - взаимнокорреляционной. Корреляционные
функциидетерминированныхпроцессовзависяттолькоот t2 t1 . |
|
|
||||||||
Если заданы сигналы s1 t |
и s2 t , то |
корреляционные функции определяют |
||||||||
следующими выражениями: |
|
|
|
|
|
|
||||
|
1 |
|
T 2 |
|
|
|
|
|
|
|
Rs1s2 |
|
T s1 t s2 |
t dt |
- взаимнокорреляционнаяфункция; |
(2.66) |
|||||
T |
|
|||||||||
|
|
2 |
|
|
|
|
|
|
||
R |
|
1 |
T 2s t s t dt |
- автокорреляционнаяфункция. |
(2.67) |
|||||
|
|
|||||||||
s |
T T |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
||
Если s1 t и s2 t |
|
- два периодических сигнала с одинаковым периодом T, |
то |
|||||||
очевидно, что их корреляционная |
функция Rs |
,s |
тоже является периодической |
с |
||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
периодом Т и, следовательно, она можетбытьразложенаврядФурье.
Действительно, если в выражении (2.66) разложим в ряд Фурье сигнал s2 t , то получим

47
|
|
|
|
|
|
|
|
|
1 |
T 2 |
|
|
|
|
|
1 |
T 2 |
|
|
|
|
|
i n 0 t |
|
|
|
||||
|
|
Rs1s2 |
|
T |
s1 |
t s2 t dt |
T |
s1 |
t C2n e |
dt |
|
|||||||||||||||||||
|
|
T |
T |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
(2.68) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
s1 t ei n 0 t dt |
|
|
|
|
|
|
, |
|
|
|||||||||||||
C2n ei n 0 |
|
T |
C1n C2n ei n 0 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
T |
|
2 |
|
|
|
n |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
s2 t |
||||||||||||||||||||||
C1n и C2n - комплексные амплитуды n-й гармоники сигналов s1 t и |
||||||||||||||||||||||||||||||
соответственно, |
|
|
|
- |
комплексно-сопряженный |
с |
|
|
коэффициент. Коэффициенты |
|||||||||||||||||||||
C |
C |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1n |
|
|
|
|
|
||||
разложения взаимно корреляционнойфункции C1n C2n можнонайтикаккоэффициентыряда Фурье
|
1 |
T 2 |
e i n 0 t dt . |
|
|
C1n C2n |
|
T Rs1s2 |
(2.69) |
||
T |
|
||||
|
|
2 |
|
|
|
Частотноеразложениеавтокорреляционнойфункциилегкополучитьизформул(2.68) и (2.69), положив s1 t s2 t s t , тогда
Rs |
1 |
T 2 |
s t s t dt |
|
|
2 ei n 0 t . |
|||||
|
T |
|
|
|
|
n |
|
||||
|
|
C |
|
||||||||
T |
|
||||||||||
|
|
|
n |
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
||
Атаккак Cn C n и, следовательно,
|
|
2 ei n 0 |
|
|
|
2 e i n 0 t , |
||||||||
|
|
|
|
n |
|
|
|
|
|
|
n |
|
||
|
|
|
|
|
||||||||||
C |
C |
|||||||||||||
n |
|
|
|
|
|
n |
|
|
|
|
||||
то автокорреляционная функция Rs - четная и поэтому
Rs C02 |
|
|
2 e i n 0 t . |
||||
2 |
|
|
|
n |
|
||
|
|
|
|||||
C |
|||||||
|
n 1 |
|
|
|
|
||
(2.70)
(2.71)
(2.72)
Четность автокорреляционной функции позволяет ее разложить в тригонометрический рядФурьепокосинусам
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Rs a0 an cos n 0 |
|
|
C0 |
|
2 2 |
|
|
|
n |
|
2 cos n 0 . |
(2.73) |
||||||
|
|
|
C |
|
||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
||
Вчастномслучае, при 0 , получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Rs 0 C02 |
|
|
|
|
2 . |
|
|
|
|
|
|
|
||||||
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
||||||
|
C |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, автокорреляционная функция при 0 представляет собой полную среднюю мощность периодического сигнала s t , равную сумме средних мощностей всех гармоник.

48
§2.10. Частотное представление импульсных сигналов
В предыдущем рассмотрении предполагалось, что сигналы непрерывны, однако при автоматической обработке информации часто используются и импульсные сигналы, а также преобразование непрерывных сигналов в импульсные. Это требует рассмотрения вопросов частотногопредставленияимпульсныхсигналов.
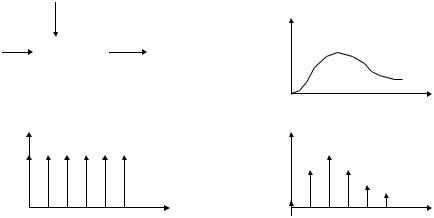
Рассмотрим модель преобразования непрерывного сигнала в импульсную форму, представленнуюнарис.2.6а.
a) |
|
u( ,t) |
в) u( ,t) |
|||
|
x(t) |
|
y(t) |
|||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) x(t) |
T |
|
г) y(t) |
|
|
|
t |
t |
|
|
Рис.2.6
Пусть на вход |
импульсного модулятора поступает непрерывный сигнал x t |
|||
(рис.2.6б). Импульсный |
модулятор формирует последовательность единичных импульсов |
|||
(рис.2.6в) с периодом Т и длительностью импульсов , |
|
причем T . Математическую |
||
модельтакойпоследовательности импульсов можно описать в виде функции u ,t : |
||||
|
1, если kT t kT |
; |
|
(2.74) |
|
u ,t |
|
|
|
|
0, если kT t k 1 T , |
|
||
|
|
|
|
|
где k - номер импульса в последовательности.
Выходнойсигналимпульсногомодулятора y t (рис.2.6г) можнопредставитьввиде: y t u ,t x t .

49
На практике желательно иметь частотное представление последовательности импульсов. Для этого функцию u ,t , как периодическую, можно представить в виде ряда Фурье:
|
|
|
|
|
u ,t |
|
|
||
|
|
|
|
|
|
|
n e j n u t , |
(2.75) |
|
|
|
|
|
|
C |
||||
|
|
|
|
|
|
n |
|
||
где |
0 |
|
|
|
|
|
|||
|
|
|
T |
|
|
|
|
|
|
|
C |
n |
1 |
T u ,t e j n u t dt |
- спектральныекоэффициентыразложенияврядФурье; |
(2.76) |
|||
|
|
||||||||
u 2T - частотаследованияимпульсов;
n - номергармоники.
Подставляяввыражение(2.76) соотношение(2.74), найдем Cn :
|
|
|
1 |
T |
u ,t e j n u t dt |
1 |
|
|
e |
j n u t |
|
|
|
1 e |
j n u |
|
||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
C |
n |
|
|
e j n u t dt |
|
|
|
|
|
|
|
|
|
, |
|||||
|
T |
T |
j n |
u |
T |
|
|
j n |
u |
T |
||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
при n 1,2,... ;
|
|
C0 |
|
1 |
T u ,t dt |
1 |
|
1 dt |
. |
|
|
|
|
|
||||||||||||
|
|
|
T |
T |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
T |
|
|
|
|
|
|
|
|||
Подставляя(2.76) в(2.74), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 e |
j n u |
|
|
|
|
|
|
j n u t |
e |
j n u |
t |
||||||||||
u , t |
|
|
|
|
|
e j n u t e |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
T |
|
j n u |
T |
|||||||||||||||||
|
|
n j n u |
|
|
|
|
n |
|
|
|||||||||||||||||
|
|
|
|
j n u t |
e |
j n u t |
e |
j n u t |
e |
j n u t |
|
|
||||||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
T |
n 1 |
2 sin n u |
|
|
|
j n u T |
|
|
|
|
|
|
|
||||||||||||
|
|
|
t sin n u 1 |
|
|
|
|
|
||||||||||||||||||
T |
|
|
|
|
|
|
|
|
|
n u T |
|
|
|
. |
|
|
|
|
|
|||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Преобразуемразностьсинусов, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
t |
n u |
|
|
|
||||||
|
|
|
4sin n |
2 |
|
cos n u |
2 |
|
|
|||||||||||||||||
u ,t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
n u T |
|
|
|
|
|
|
|
||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Введемобозначениефазыn-ойгармоники
u 2 .
Тогда
(2.77)
(2.78)
(2.79)
(2.80)
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin n |
|
|
||
u ,t |
|
2 |
|
|
T |
cos n u t . |
(2.81) |
|
T |
|
|
|
|||||
|
|
T n 1 |
n |
|
|
|
||
|
|
|
|
T |
|
|
|
|
Таким образом, последовательность единичных импульсов содержит |
наряду с |
|||||||
постоянной составляющей бесконечное число гармоник с уменьшающейся амплитудой. Амплитудаk-ойгармоникиопределяетсяизвыражения:
|
|
|
|
|
|
|
|
|
2 |
|
sin k |
|
|
||
A |
|
|
|
T |
. |
(2.82) |
|
T |
|
|
|
||||
k |
|
|
|
|
|
||
|
|
|
k T |
|
|
|
|
|
|
|
|
|
|
|
|
При цифровой обработке сигналов |
проводится дискретизация |
(квантование) по |
|||||
времени, то есть преобразование непрерывного сигнала в последовательность коротких импульсов. Какпоказановыше, любаяпоследовательностьимпульсовимеетдовольносложный спектр, поэтому возникает естественный вопрос, каким образом процесс дискретизации по временивлияетначастотныйспектрисходногонепрерывногосигнала.
Для исследования этого вопроса рассмотрим математическую модель процесса дискретизацииповремени, представленную на рис.2.7а.
Импульсный модулятор (ИМ) представляется в виде модулятора с несущей в виде идеальной последовательности оченькоротких импульсов (последовательности -функций)T t , период следования которых равен Т (рис.2.7б).
На вход импульсного модулятора поступает непрерывный сигнал x t (рис.2.7в),
а на выходе образуется импульсный сигнал x t (рис.2.7г).
a) |
T(t) |
в) x(t) |
|
x(t) |
|
|
x (t) |
|
И.М. |
||
|
|
|
t |
|
|
|
|
б) T(t) |
|
г) x (t) |
|
0 T 2T 3T 4T 5T |
t |
T 2T 3T 4T 5T |
t |
Рис.2.7
