
- •Механика (общая характеристика).
- •Кинематика поступательного движения (способы описания).
- •Кинематика прямолинейного движения (уравнение, характеристика основных величин).
- •Кинематика вращательного движения (уравнение, характеристика основных величин).
- •Кинематика сложного движения (общая характеристика).
- •Инерциальная система отсчета (исо). Законы динамики в исо.
- •Определение момента инерции материальной точки и твердого тела.
- •Определение момента силы относительно неподвижной оси вращения.
- •Определение момента силы относительно точки.
- •Выведите формулу момента инерции диска.
- •Формулировка теоремы Штейнера. Поясните величины, входящие в формулу Штейнера.
- •Определение момента импульса материальной точки и твердого тела относительно неподвижной оси вращения.
- •Напишите таблицу аналогий для поступательного и вращательного движений и поясните соответствующие величины.
- •Уравнение динамики движения тела в поступательно движущейся неинерциальной системе отсчета.
- •Силы инерции во вращающихся системах отсчета.
- •Работа силы в поступательном движении.
- •Работа силы во вращательном движении.
- •Сформулируйте три условия консервативности силового поля.
- •Потенциальная энергия.
- •Работа силы и ее связь с принципами симметрии.
- •Закон сохранения момента импульса. С каким принципом симметрии он связан?
- •Гравитационное поле, его характеристики: напряженность и потенциал.
- •Принцип относительности Галилея.
- •Систематические ошибки измерений.
- •Статистические характеристики случайных погрешностей.
- •Доверительный интервал. Коэффициент Стьюдента. С какой целью он вводится?
- •Как определяются ошибки при косвенных измерениях?
- •Суммарная ошибка прямых измерений. Частные случаи.
- •Постулаты специальной теории относительности.
- •Пространственно-временной интервал. Что означает инвариантность?
- •Запишите, сформулируйте и объясните закон Кулона.
- •Дайте определение напряженности электрического поля. Каково направление вектора напряженности? Нарисуйте вид поля для заряженных а) плоскости; б) сферы; в) цилиндра. Принцип суперпозиции.
- •Как определяется вектор электрического смещения? Что он характеризует?
- •Дайте определение потенциала и разности потенциалов электрического поля.
- •Связь напряженности электрического поля с разностью потенциалов.
- •В чем заключается явление поляризации диэлектрика? Виды поляризации. Характеристики поляризации.
- •Дайте определение дипольного момента.
- •Запишите и сформулируйте теорему Гаусса для вектора напряженности электрического поля.
- •Запишите, сформулируйте и объясните теорему Гаусса для вектора электрического смещения.
- •Проводники в электрическом поле (общая характеристика).
- •Дайте определение емкости уединенного проводника и конденсатора.
- •Энергия электрического поля.
- •Электрический ток: определение, его виды и характеристики.
- •Что такое сторонние силы? Какова их природа? Дайте определение эдс.
- •Когда напряжение и разность потенциалов совпадают?
- •Обобщенный закон Ома. Рассмотрите частные случаи.
- •Эдс, напряжение, разность потенциалов (физический смысл).
- •Законы Кирхгофа.
- •Импульс. Закон сохранения импульса.
- •Закон Джоуля-Ленца.
- •Закон Менделеева-Клапейрона.
- •Формулы скорости молекул, среднего числа столкновений, средней длины свободного полета.
- •Закон Больцмана, теплоемкость.
- •Применение первоначала термодинамики к изопроцессам. Адиабатический процесс.
-
Определение момента силы относительно неподвижной оси вращения.
Моментом силы относительно неподвижной
оси z называется скалярная величина Mz,
равная проекции на эту ось вектора
 момента силы, определенного относительно
произвольной точки О данной оси z.
Значение момента Мz не зависит от выбора
положения точки О на оси z. Если ось z
совпадает с направлением вектора М, то
момент силы представляется в виде
вектора, совпадающего с осью:
момента силы, определенного относительно
произвольной точки О данной оси z.
Значение момента Мz не зависит от выбора
положения точки О на оси z. Если ось z
совпадает с направлением вектора М, то
момент силы представляется в виде
вектора, совпадающего с осью:
 =[
=[ ]z.
]z.
-
Определение момента силы относительно точки.
Моментом силы относительно неподвижной
точки О называется физическая величина
М, определяемая векторным произведением
радиус-вектора r, проведенного из точки
О в точку приложения силы, на силу F:
 =[
=[ ],
где
],
где
 – псевдовектор, его направление совпадает
с направлением поступательного движения
правого винта при его вращении от
– псевдовектор, его направление совпадает
с направлением поступательного движения
правого винта при его вращении от
 к
к
 .
.
Модуль момента силы M=Frsinα=Fl, где α – угол между r и F, а l – кратчайшее расстояние между точкой О и линией действия силы – плечо силы.
-
Выведите формулу момента инерции диска.
Диск – плоский однородный цилиндр
высотой h и радиусом R. Разобьем диск на
отдельные кольца бесконечно малой
толщины dr с внутренним радиусом r и
внешним r+dr. Момент инерции каждого
кольца dJ=r2dm, объем
кольца 2πrhdr. Если ρ –
плотность материала, то dm=2πrhρdr
и dJ=2πhρr3dr.
Тогда момент инерции всего диска J=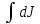 =
= = 1/2πhρR4. Но масса
диска m=πhρR2, тогда
момент инерции диска J=1/2mR2.
= 1/2πhρR4. Но масса
диска m=πhρR2, тогда
момент инерции диска J=1/2mR2.
-
Формулировка теоремы Штейнера. Поясните величины, входящие в формулу Штейнера.
Момент инерции тела относительно произвольной оси (Jz) равен сумме момента инерции относительно параллельной оси, проходящей через центр масс тела (Jc) и произведения массы тела на квадрат расстояния между осями: Jz=Jc+md2
Jz – момент инерции относительно произвольной оси
Jc – момент инерции относительно оси, проходящей через центр масс
d – расстояние между осями
m – масса тела
-
Определение момента импульса материальной точки и твердого тела относительно неподвижной оси вращения.
Моментом импульса относительно
неподвижной оси z называется скалярная
величина Lz, равная проекции на эту ось
вектора момента импульса
 =[
=[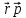 ]=[
]=[ ,
m
,
m ],
определенного относительно произвольной
точки О данной оси. Момент импульса Lz
не зависит от положения точки О на оси
z.
],
определенного относительно произвольной
точки О данной оси. Момент импульса Lz
не зависит от положения точки О на оси
z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса ri с некоторой скоростью vi. Скорость vi и импульс mivi перпендикулярны тому радиусу, т.е. радиус является плечом вектора mivi. Поэтому можно записать Liz= miviri и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц: Lz=
 =
= =ω
=ω =Jzω
=Jzω
-
Напишите таблицу аналогий для поступательного и вращательного движений и поясните соответствующие величины.
Масса m – момент инерции J
Скорость v=dr/dt – угловая скорость ω=dϕ/dt
Ускорение a=dv/dt – угловое ускорение ε=dω/dt
Сила F – Момент силы Mz или M
Импульс p=mv – момент импульса Lz=Jzω
Основное уравнение динамики: F=ma – Mz=Jzε
Работа: dA=Fsds – dA=Mzdϕ
Кинетическая энергия: mv2/2 - Jzω2/2
