9.Экстремальные свойства энтропии непрерывных

сообщений.

Если заданы пределы изменения символов непрерывного сообщения, то можно найти функцию плотности распределения вероятности символов (p(x)), обращающую энтропию непрерывного сообщения H_x в максимум.

Пусть непрерывное сообщение представляет собой ограниченную непрерывную функцию с областью значений из интервала [а;b] (рис.3) и с неизвестной плотностью распределения вероятностей символов p(x), удовлетворяющую равенству

(42)

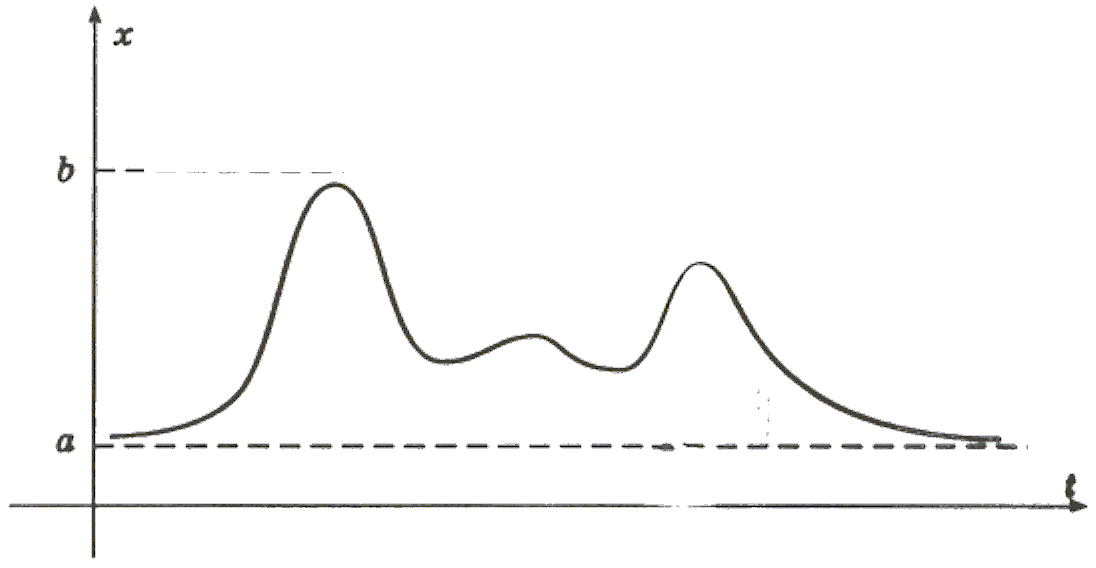
Рис. 3

Поставим задачу найти распределение p_max(x), при котором дифференциальная энтропия этого сообщения

принимает максимальное значение.

Для решения этой задачи воспользуемся методом неопределенных множителей Лагранжа.

Составив функцию Лагранжа

,

продифференцировав ее по p(p не зависит от x, поэтому достаточно продифференцировать подынтегральное выражение), на основании необходимого условия существования экстремума получим:

.

Откуда после несложных преобразований

имеем:

при (43)

Подставив это выражение в (42) получим:

,

а используя равенство (43) находим:

, при . (44)

Следовательно, искомая функция плотности распределения вероятности (p_max(x)) запишется в виде:

45)

Таким образом, энтропия непрерывного сообщения принимает свое максимальное значение при равновероятном появлении всех символов, принадлежащих интервалу [а;b]. При этом максимально возможное значение энтропии будет определяться по формуле

. (45)

10.Информация в непрерывных сообщениях

при наличии шумов

Рассмотрим модель источника непрерывных сообщений, представленную на рис.4, где:

1 — источник непрерывных зашумленных сообщений;

2 — идеальный источник непрерывных сообщений;

3 — сумматор.

Выходное сообщение такого устройства (у) представляет со бой смесь идеального непрерыв- ного сообщения (х) и шума (n).

Будем рассматривать част - ный случай, когда шумы и по- мехи носят аддитивный харак - тер, то есть когда выходное со - Рис.4 общение (у) есть сумма идеального сообщения (х) и шума (n):

y = x + n

Для определения качества информации, содержащегося в каком- либо конкретном символе непрерывного сообщения (I), можно вос- пользоваться соотношением (2):

где — априорная вероятность появления символа сообщения;

—апостериорная вероятность появления того же символа со- общения.

В случае непрерывного сообщения х под априорной вероятностью следует подразумевать вероятность того, что символ сообщения заключен в интервале значений между х и . Если функция плотности распределения вероятности символов исходного сообщения есть р(х), то априорная вероятностьможет быть найдена из выражения(46) (46) а апостериорную вероятность сообщения можнопредставить в виде:

(47)

где — условная плотность распределения вероятностей символов сообщениях, когда известен символ у.

Подставляя в формулу (2) значенияивычисленные соответственно по формулам (46) и (47), и переходя к пределу при,получим

(48)

Следует подчеркнуть, что определяемое этой формулой количество информации I соответствует только одной паре возможных значений х и n. Так как и сообщение и помеха могут принимать бесконечное число различных, не связанных между собой значений, то для оценки средней информации, получаемой при приеме сообщения на фоне аддитивного шума, необходимо усреднить выражение (48) по всем возможным значениям х и n.

Для этого используем известные соотношения теории вероятностей. Так, совместная плотность распределения вероятностей событий

x и y определяется выражением

P(x,y)=p_y(x)∙p(y)= p_x(y)∙p(x), (49)

где p(y-) плотность распределения вероятности символов в сообще

нии y=x+n, когда переданное сообщение есть x;

p_y(x)- условная плотность распределения символов в сообщении

x , когда принятое сообщение есть y.

При этом можно получить следующие соотношения

(50)

Кроме того, из (49) следует

(51)

Подставляя этот результат в (48) получаем:

С учетом того, что p_x(y)∙dy=P_x(y) есть условная вероятность появления сообщения y_x в интервале , когда передаваемое сообщение естьx, и p(y)∙dy=P(y)- вероятность того, что сообщение y содержится в интервале при неизвестномx, предыдущее выражение преобразуется к виду

(52)

Это соотношение определяет количество информации, получаемой при передаче сообщения x, когда при приеме наблюдателю известна сумма y=x+n.

Заметим, что p_x(y)∙по существу есть не что иное, как плотность распределения вероятностей шума n. Действительно, если задан конкретный символ сообщения x₀, то сумма y=x₀+n распределена по закону распределения шума n, который наложен на символ сообщения x₀, а значит,

p_x(y)∙= p(n). (53)

После подстановки в (52) имеем:

. (54)

Теперь для оценки среднего количества информации при приеме сообщения на фоне шума (I) необходимо путем интегрирования по всем значениям x и y усреднить количество информации, приходящееся на каждое распределение вероятностей p(x,y).

(55)

Очевидно, что плотность распределения вероятностей шума (n) не зависит от x и y по отдельности, а определяется только их разностью, т.к. n= y- x. Кроме того, учитывая (53), соотношение (49) можно преобразовать к виду

P(x,y)= p_x(y)∙p(y)=p(n)∙p(x), (56)

тогда первое слагаемое в (55) можно записать в следующем виде:

Во внутреннем интеграле dy заменено на dn , т.к. y=x +n, а при интегрировании по y величина x рассматривается как постоянная.

В такой записи внутренний интеграл представляет собой взятую со знаком минус энтропию шума H(n).

При стационарном шуме энтропия шума является величиной постоянной и может быть вынесена за знак интеграла, тогда первое слагаемое в выражении (55) преобразуется к виду:

(57),

т.к.

(58)

Обратимся теперь ко второму слагаемому выражения (55). Используя равенство (50)

,

можем написать

(59)

Окончательно получаем

, (60)

т.е. среднее количество информации в символе сообщения x, которую можно извлечь из смеси y= x+ n равна разности энтропий принятого сообщения y и шума n.

При длительности сигнала T на одну секунду приходится, в сред- нем информация

. (61)