33. Частица в одномерной прямоугольной потенциальной яме. Квантование состояний.

П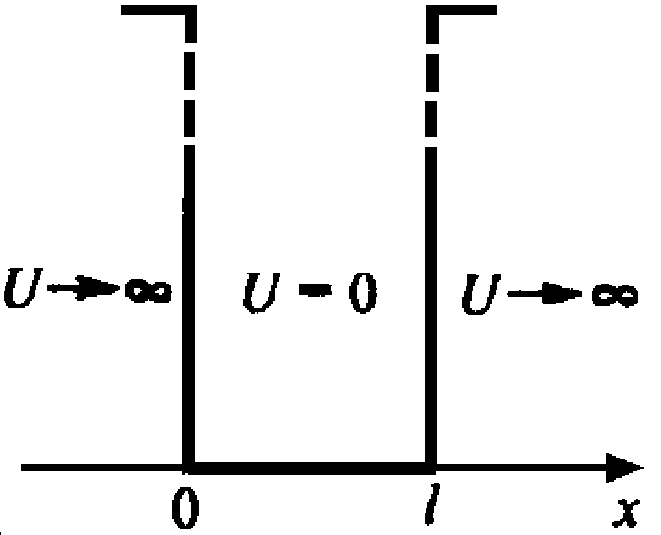ространственно ограниченное квантовое движение- одномерное движение чатицы, находящейся в силовом поле, энергия взаимодействия с которым имеет вид бесконечно глубокой потенциальной ямы с вертикальными стенками. Находясь внутри ямы, частица движется свободно на участке , а на краях силовое поле возвращает ее обратно в яму.

Потенциальная яма, где - ширина ямы, а энергия отсчитывается от ее дна. Никакая частица не может выйти из этой ямы. Если частица классическая , то на участке она движется с неизменным импульсом и энергией. Достигая стенок ямы, частица испытывает упругий удар и меняет направление на противоположное. Частота таких колебаний частицы зависит от скорости частицы и ширины ямы . В зависимости от скорости, если

1) , То положим равной 0; 2): частица движется между стенками, и график плотности распределения вероятности будет выглядеть в виде прямой (см. Рисунок).

Для реальной частицы: запишем уравнение Шредингера, учитывая что внутри ямы U=0: . За пределы ямы частица не проникает, поэтому волновая функция вне ямы равна 0, следовательно, на границах ямы . С учетом граничных условий волновая функция должна представлять собой стоячую волну. Решение ищем в виде . . . По второму граничному условию: . , где n - квантовое число. Для определения const C используем условие нормировки: , т. к. вероятность обнаружения частицы внутри ямы равна 1, следовательно . Как видно, волновые функции обращаются в ноль на границах ямы. Внутри ямы они представляют собой отрезки синусоиды. Основное условие, котрое должно выполняться,- на ширине ямы должно укладываться целое количество для каждой синусоиды. Количество этих половинок определяется значением целого числа n. Анализ графиков показывает, что вероятность нахождения квантовой частицы в потенциальной яме зависит от координаты x. Так в случае n=1 наибольшая вероятность существует для центра ямы и т.д. Получили, что если у классической частицы плотность вероятности внутри потенциальной ямы всюду одинакова, то у квантовой частицы она является функцией координат. Рассмотрим Е: из граничных условий, то, где , т. е. есть множество значений энергии, которые частица не принимает. Таким образом, энергия дискретна, т. е. квантована. Чем меньше , тем выше ; состояния частицы дискретны. Энергия пробегает ряд значений, не равных 0. Разрешенные энергии частицы называются энергетическими уровнями, они появляются, если частица ограничена в пространстве. Разность энергий двух соседних уровней . С увеличением n соседние уровни удаляются друг от друга. Величина энергетического зазора между уровнями зависит также от массы частицы m и ширины ямы l. Чем меньше эти величины, тем больше расстояние между уровнями. С увеличением ширины ямы или массы частицы уровни сгущаются и их дискретность все менее заметна. В пределе беск широкой ямы или частицы с беск большой массы получаем классический непрерывный спектр энергии.

Изобразим волновую функцию на фоне уравнений при .

- основное состояние (основной энергетический уровень).

У классической частицы этот график выглядит в виде прямой, параллельной оси Ох. Минимальное значение энергии . Состояние частицы с такой энергией называется основным состоянием. То, что квантовая частица не может иметь энергию, равную нулю согласуется с принципом неопределенности. Волновая функция и энергия состояния квантовой частицы в потенциальной яме однозначно определяются величиной целого числа n, которое определяется квантовым числом системы.