
- •15. Гармонический осциллятор. Энергия гармонического осциллятора.
- •21. Поперечные волны на дискретной струне. Явление дисперсии. Фазовая и групповая скорость волн.
- •28. Тепловое излучение, его характеристики и закономерности. Подход Рэлея-Джинса. Гипотеза планка.
- •32. Отражение частиц от потенциальной ступеньки. Туннельный эффект.
- •33. Частица в одномерной прямоугольной потенциальной яме. Квантование состояний.
- •1) , То положим равной 0; 2): частица движется между стенками, и график плотности распределения вероятности будет выглядеть в виде прямой (см. Рисунок).
- •34. Частица в двумерной потенциальной яме. Вырождение состояний.
14. Гармонические колебания и формы их представления. Сложение гармонических колебаний. Биения, фигуры Лиссажу.
Гармонические колебания
В общем случае состояние системы изменяется. Если в изменение обнаруживается повторяемость, то в системе происходят колебания. Если колебания повторяются через строго определенный промежуток времени, то такое колебание периодическое, а сам промежуток – это период Т. Колебания, происходящие по закону Sin или Cos называются гармоническими.
Причины гармонических колебаний:
-
Многие колебания во многих системах близки к гармоническим.
-
Любое произвольное колебание можно представить в виде суммы гармонических колебаний.
Характеристики и способы представления гармонических колебаний
-
Аналитическое:
![]()
-
Графическое:
x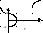 –
смещение;
–
смещение;
A - амплитуда (максимальное значение x);
![]() -
фаза;
-
фаза;![]() - начальная фаза, при t
= 0, зависит от состояния система и
времени;
- начальная фаза, при t
= 0, зависит от состояния система и
времени;
![]() -
скорость изменения фазы с течением
времени, циклическая частота;
-
скорость изменения фазы с течением
времени, циклическая частота;

-
Векторное:
Применяется для сложных колебаний. Угловая скорость – циклическая частота.
![]()

-
Комплексное:
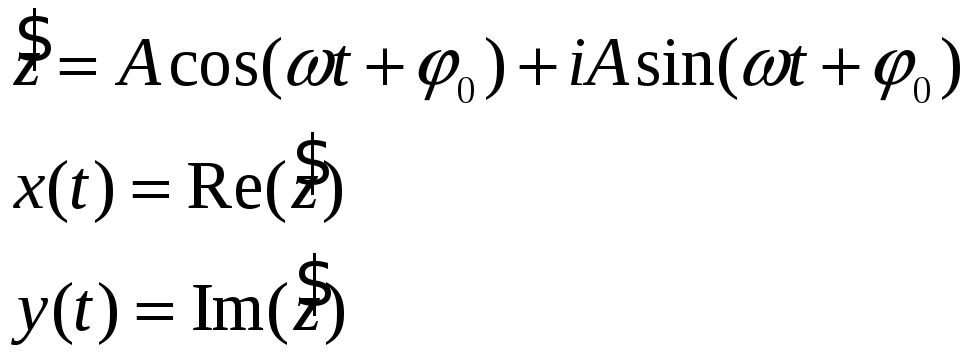
-
Показательное:
 Сложение
колебаний
Сложение
колебаний
-
Сложение однонаправленных колебаний с одинаковыми частотами:
Пусть
система принимает участие в двух
однонаправленных колебаниях с одной
![]() .
.


Сколько бы гармонических колебаний ни складывалось, получаем гармоническое колебание с такой же частотой, но у него своя амплитуда, которая зависит от амплитуды складываемых колебаний и от начальных фаз.
-
Сложение однонаправленных колебаний с разными частотами. Биения.
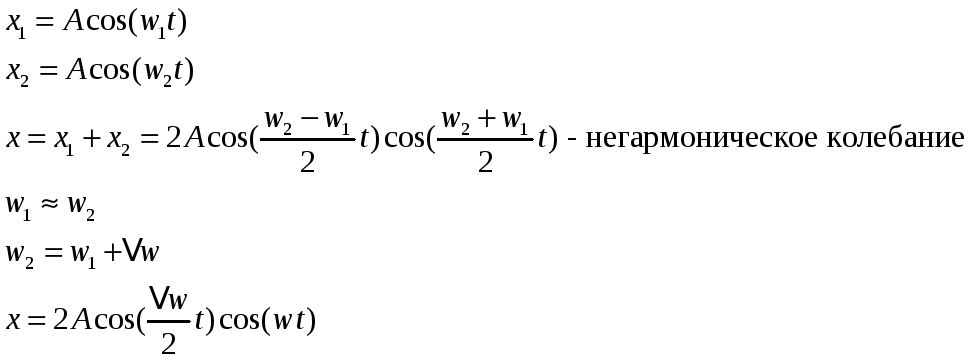 Результирующее
x
– это быстрое колебание с медленно
изменяющейся амплитудой.
Результирующее
x
– это быстрое колебание с медленно
изменяющейся амплитудой.
![]()

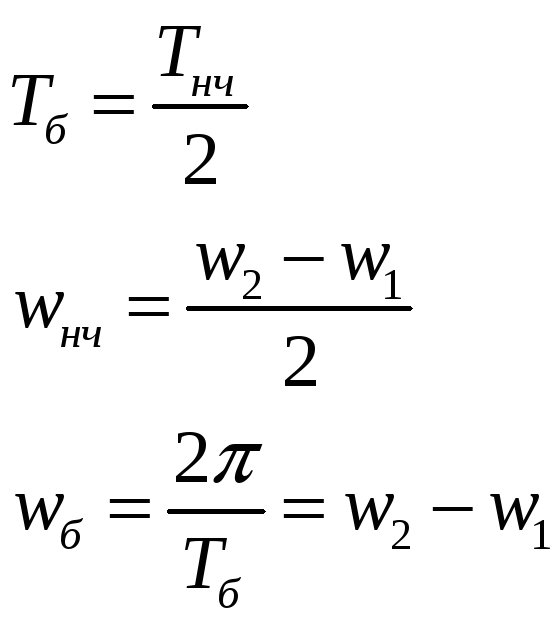 Если
амплитуды разные, то нулевой амплитуды
не получится. Если складываются колебания
с разными частотами, то получаются не
гармонические колебания.
Если
амплитуды разные, то нулевой амплитуды
не получится. Если складываются колебания
с разными частотами, то получаются не
гармонические колебания.
Сложение взаимно перпендикулярных колебаний
Разные
![]()
Результирующее
движение в общем случае сложное.
Траектория может получиться не замкнутой.
Замкнутая, если
![]() - кратны друг другу или частоты относятся,
как целые числа,
- кратны друг другу или частоты относятся,
как целые числа,
![]() ,
тогда получится фигура Лиссажу.
,
тогда получится фигура Лиссажу.
Пример:
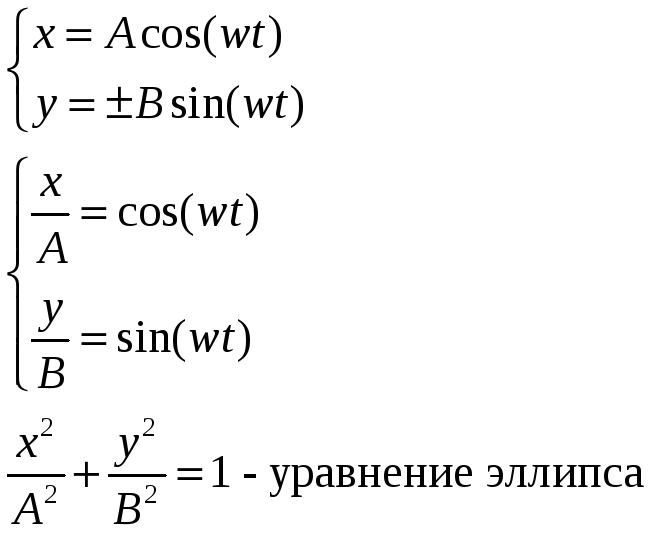
В общем случае фигура Лиссажу пересекает целое число раз каждую ось. Тогда частоты колебаний относятся между собой так, как относятся обратные числа:
![]()
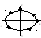
15. Гармонический осциллятор. Энергия гармонического осциллятора.
Гармонические осцилляторы.
Среди любых систем можно выделить колебательную систему или осциллятор.
Такая система может совершать колебания сама по себе, те за счет внутренних причин, если у нее есть энергия. Если собственные колебания системы являются гармоническими то система- осциллятор.
Динамика гармонических колебаний описывается дифуром:
![]() (1)
(1)
Если для системы получается уравнение (1) то система – гармонический осциллятор.
![]() -
собственная частота.
-
собственная частота.
Дифференциальное уравнение гармонического осциллятора.
![]()
![]() =>
=>
![]() - решение этого уравнения есть функции
вида
- решение этого уравнения есть функции
вида
![]() ,
,
![]() .
.
Пример 1 (Пружинный маятник.)
![]()
![]()
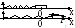
![]()
![]() -
дифференциальное уравнение гармонического
осциллятора.
-
дифференциальное уравнение гармонического
осциллятора.
![]()
![]()
Решением
дифференциального уравнения будет![]() .
.
Величина собственной частоты зависит от свойств системы.
Причин колебаний 2:
-
возвращающая сила.
-
инертность.
![]()
3 свойства осциллятора:
1. Начальное положение.
2. Возвращающая сила.
3. Инертность.
Пример 2 (Физический маятник).
Р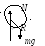 авновесие
когда
авновесие
когда
![]()
![]()
![]()
![]()
![]()
![]()
Если угол мал то:
![]()
![]() -
собственная частота.
-
собственная частота.
Пример 3 (Колебательный контур)
Сообщение заряда колебательному контуру выводит систему из положения равновесия.
![]()
 -
закон Кирхгофа.
-
закон Кирхгофа.
![]()
![]() =>
=>![]()
![]()
Возвращающие воздействие связанно с зарядом.
Энергия гармонического осциллятора.
Рассмотренные в примерах осцилляторы являются консервативными системами. Энергия с течением времени не меняется.
Пример 1.
![]()
![]() =>
=>
![]()
![]()
![]()
![]()
![]() продифференцируем
по x
и получим
продифференцируем
по x
и получим
![]() .
.
Причины, по которым получается именно это уравнение:
1) система консервативна.
2) Энергия – квадратичная форма от смещения и скорости.
Для
колебательного контура:![]()
16. Осциллятор с трением. Режимы движения. Затухающие колебания и их характеристики.
В реальных осцилляторах есть трение, трение трансформирует энергию колебаний во внутреннюю энергию. При достаточно большом трении колебаний может и не быть.
Дифференциальное уравнение осциллятора с трением
-
Колебательный контур
![]()
 ;
;
![]() ;
;
![]()
-
Пружинный маятник
П![]() ружинный
маятник движется в некоторой среде,
тогда на маятник будет действовать сила
сопротивления, модуль которой
ружинный
маятник движется в некоторой среде,
тогда на маятник будет действовать сила
сопротивления, модуль которой
![]() .
.
![]()
![]() ;
;![]() ;
;
![]()
В общем случае дифференциальное уравнение осциллятора с трением:
(1)
![]() ,
где
,
где
![]() -
квадрат собственной частоты,
-
квадрат собственной частоты,
![]() -
коэффициент затухания.
-
коэффициент затухания.
дифференциальное уравнение осциллятора с трением описывает собственную динамику осциллятора, у которого трение линейно зависит от скорости.
Режимы осциллятора с трением
Характер движения осциллятора с трением. Если трение очень маленькое, то колебания должны быть, но их амплитуда должна падать. Если трение велико, то колебаний может не быть.
Решение (1) будем искать в виде x=Aet.
![]() Aet
(2+2+
Aet
(2+2+![]() )=0
)=0
2+2+![]() =0
1,2=
=0
1,2=![]()
Возможны
три ситуации, связанные с коэффициентами
![]() и
и
![]() ,
и они соответствуют трем возможным
режимам осциллятора с трением:
,
и они соответствуют трем возможным
режимам осциллятора с трением:
-
Апериодический режим
 >
>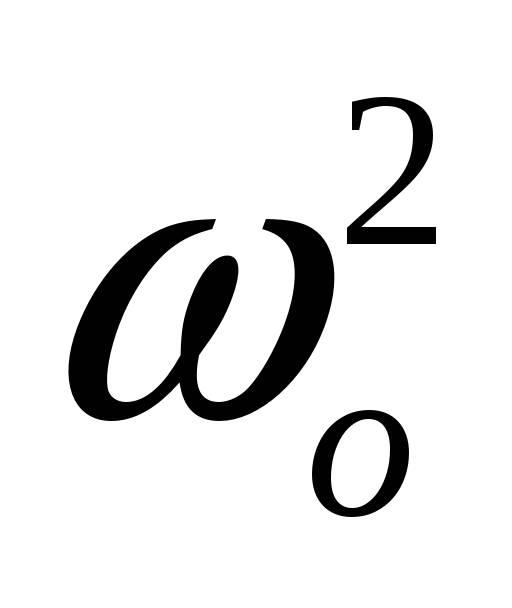
1<0,
1<0
x(t)= A1eg1t+ A2eg2t= A1e(![]() )*t+
A2e(
)*t+
A2e(![]() )*t
)*t
Апериодический режим возникает при большом трении в системе.
-
Режим критического затухания.
b=![]() 1=2=-b x(t)=(A+Bt)e-bt
Вид картины такой же.
1=2=-b x(t)=(A+Bt)e-bt
Вид картины такой же.
В![]() режиме критического затухания система
наиболее быстро возвращается в положение
равновесия среди апериодических режимов.
режиме критического затухания система
наиболее быстро возвращается в положение
равновесия среди апериодических режимов.
Коэффициент сопротивления r называется критическим коэффициентом затухания, b – коэффициент критического затухания, R- критическое сопротивление контура.
Найдем выражение для критического сопротивления:
bкр=
![]() ;
;
![]() ;
;
![]()
-
Режим затухающих колебаний.
b<
![]() ;
1,2=
;
1,2=![]() ,
где
,
где
![]()
![]()
x(t)=Re(![]() (t))=
A1e-btcos(wt+01)+
A2e-btcos(wt+02)=
A0e-btcos(wt+0)
(t))=
A1e-btcos(wt+01)+
A2e-btcos(wt+02)=
A0e-btcos(wt+0)
A0 – зависит от энергии.
0 – зависит от начального состояния системы.
Затухающие колебания и их характеристики
b<
![]() x(t)= A0e-btcos(wt+0)
x(t)= A0e-btcos(wt+0)
Положим 0=0.
Колебания не периодичны (т.к. max не повторяются), но они характеризуются периодом затухающих колебаний.
T=![]() ,
,
![]() -
зависит не только от возвращающего
воздействия, но и от трения.
-
зависит не только от возвращающего
воздействия, но и от трения.
![]() -
постоянная времени затухания(времени
релаксации) – за это время амплитуда
уменьшается ровно в e
раз.
-
постоянная времени затухания(времени
релаксации) – за это время амплитуда
уменьшается ровно в e
раз.
![]() ;
A=A0e-1;
;
A=A0e-1;
![]() =1;
=
=1;
=![]()
- логарифмический декремент затухания.
=![]() ,
=
,
=![]()
обратно числу колебаний, в течении которых амплитуда уменьшается в e раз.
//продолжение ниже//
Энергия затухающих колебаний. Добротность колебательной системы.
Энергия осциллятора с трением:
E=kA2/2; A=A0e-t
E=![]()
Чтобы характеризовать уменьшение энергии в системе вводится понятие добротности.
Q – добротность. Есть три определения добротности:
-
Q=
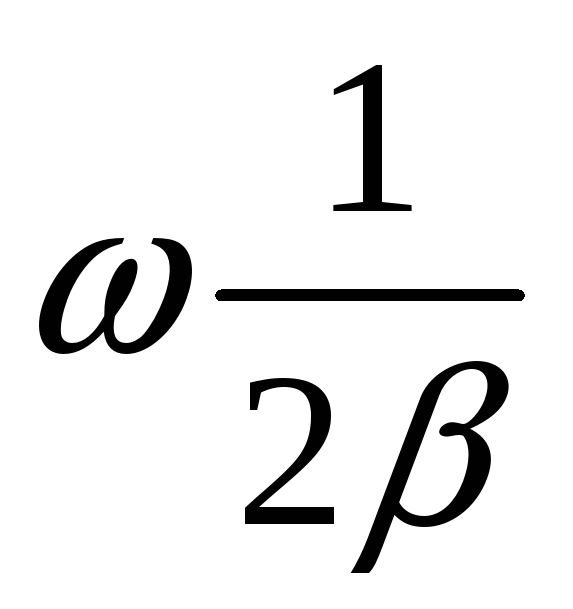
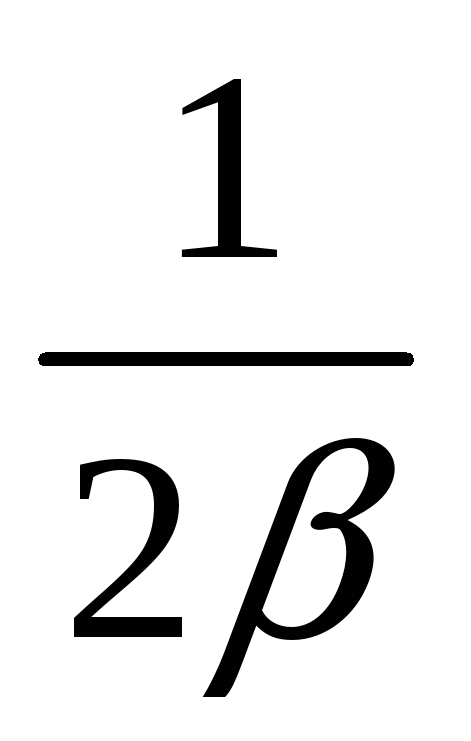 -
время, за которое энергия уменьшается
в e
раз.
-
время, за которое энергия уменьшается
в e
раз.
При таком определение добротность численно равна изменению фазы колебаний за время, в течении которого энергия уменьшается в e раз.
-
<<o; Q=
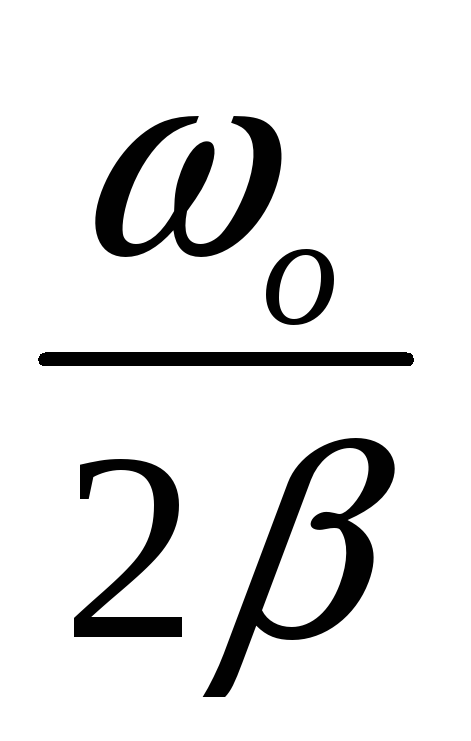 .
. -
Пусть трение мало, найдем изменение энергии за период.
E=![]() ;
;
![]() ;
;
![]() ;
;
![]()
17. Вынужденные колебания осциллятора. Резонанс. Импеданс колебательной системы.
Осциллятор может находиться под внешним воздействием. Если воздействие гармоническое, то реакция осциллятора избирательна. Степень воздействия зависит от частоты воздействия.
Если частота воздействия равна собственной частоте о, то это воздействие будет максимальным, и получило название резонанса.
Д ифференциальное
уравнение вынужденных колебаний
ифференциальное
уравнение вынужденных колебаний
-
Пружинный маятник
Focos(t) – внешнее гармоническое воздействие
![]() ;
;
![]() ;
;
![]()
-
К
L
олебательный контур
![]()
![]() ;
q/c+RI=-L
;
q/c+RI=-L![]() ;
;
![]()
В
общем случае дифференциальное уравнение
вынужденных колебаний:
![]()
Дифференциальное уравнение вынужденных колебаний неоднородно. Справа не ноль. Общее решение неоднородного уравнения складывается из двух, а именно: решения общего однородного уравнения и частного решения неоднородного уравнения.
Нас интересует частного решения неоднородного уравнения, которое определяет установившееся решение.
Справа гармоническая функция, слева сумма трех функций, которые тоже должны быть гармоническими с той же частотой.
Характеристики вынужденных колебаний
![]() x(t)=Re(x(t))
x(t)=Aoeit=Aoeioeit
x(t)=Re(x(t))
x(t)=Aoeit=Aoeioeit
Осуществим подстановку:
x/(t)=iAoeit x//(t)=- 2Aoeit Aoeiwt(-2+2iw+wo2)=foeiwt
Ao=![]() Ao=
Ao=![]() ;
;
![]() .
Частное решение уравнения имеет вид:
.
Частное решение уравнения имеет вид:
x(t)=
![]() cos(wt+
cos(wt+![]() )
)
Вынужденные колебания в системе оказались сдвинутыми по фазе по отношению к вынужденному воздействию.
х=Acos(wt+o)
-
Частота колебаний равна частоте вынужденных колебаний
-
A(w) – амплитуда зависит от частоты воздействия. При разных частотах А(w) будет разной.
-
о – разность фаз этого колебания и колебания вынужденного воздействия.
Амплитуда вынужденных колебаний. Явление резонанса.
-
Низкие частоты: w существеннее меньше wо.
![]() (на
примере маятника)
(на
примере маятника)
При
низкой частоте реакция на внешнее
воздействие зависит от упругих свойств
системы и от возвращающего воздействия.
![]() -
статическое
смещение
-
статическое
смещение
-
Высокие частоты: w существеннее больше wо.
![]() При
высоких частотах определяющим является
инертность системы. Чем больше инертность,
тем амплитуда колебаний меньше.
При
высоких частотах определяющим является
инертность системы. Чем больше инертность,
тем амплитуда колебаний меньше.
-
У зависимости А(w) должен быть максимум. Амплитуда максимальна, когда
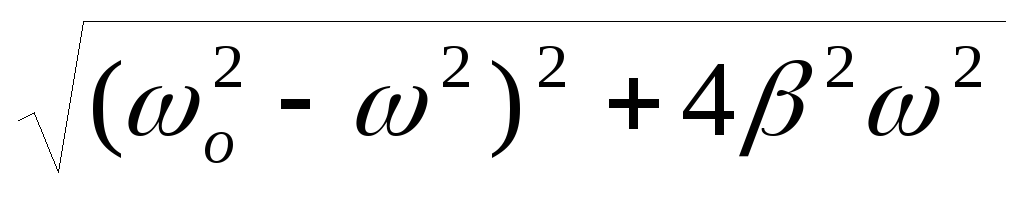 минимальна.
минимальна.
wо, , fo – const, мы их зафиксировали.
![]()
w1=0
w2=![]() -
резонансная частота.
-
резонансная частота.
Когда частота воздействия равна резонансной частоте, тогда будет максимум амплитуды.
![]() =0,
при выполнении этого условия явление
резонанса исчезает. Если трение велико,
то резонанса не будет.
=0,
при выполнении этого условия явление
резонанса исчезает. Если трение велико,
то резонанса не будет.
Резонанс скорости
х=Acos(wt+jo)
v=![]() vA=
vA=![]()
1)
![]() низкие частоты.
низкие частоты.
![]() ,
т.е. движения нет.
,
т.е. движения нет.
2)
![]()
![]()
Между w и vA должен быть максимум, следовательно резонанс скорости должен быть при любом значении трения.
VA=![]()
Скорость будет максимальной, когда частота вынужденного воздействия равна собственной частоте.
Резонанс скорости существует всегда при любом трении. От резонанса скорости в принципе нельзя избавиться, также существует резонанс ускорения.
В условиях малого можно
считать, что все частоты приблизительно
равны w0.
условиях малого можно
считать, что все частоты приблизительно
равны w0.

![]()
Фаза вынужденных колебаний.
F
= F0cos(t),
x
= Acos(t+![]()
-
=0, 0=0
-
При произвольной частоте 0<0, т.е. колебания которые установятся в этой системе будут отставать по фазе от колебания воздействия.
= - характерная точка. В этом случае max одной системы приходится на 0 в другой и наоборот. F = F0cos(t), x = Acos(t - /2)
Добротность и резонансные свойства системы
Резонансные свойства системы можно характеризовать добротностью.
Арез – резонансная частота Аст – статическое смещение
-
Аст , когда w = 0; Аст=
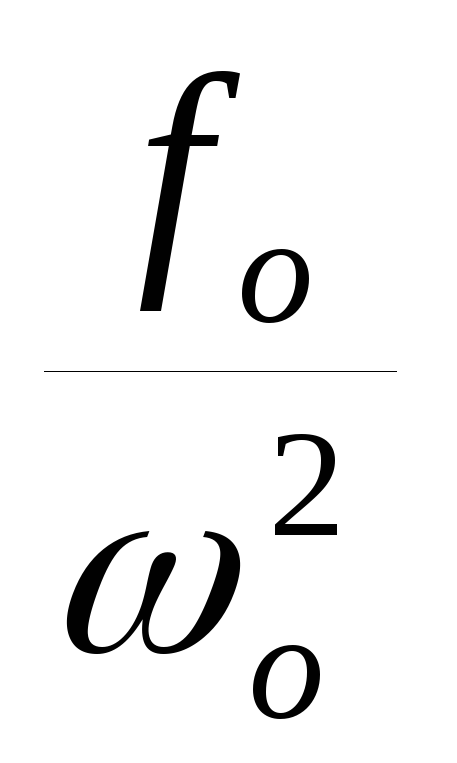
-
Арез, когда w= wо; Арез=
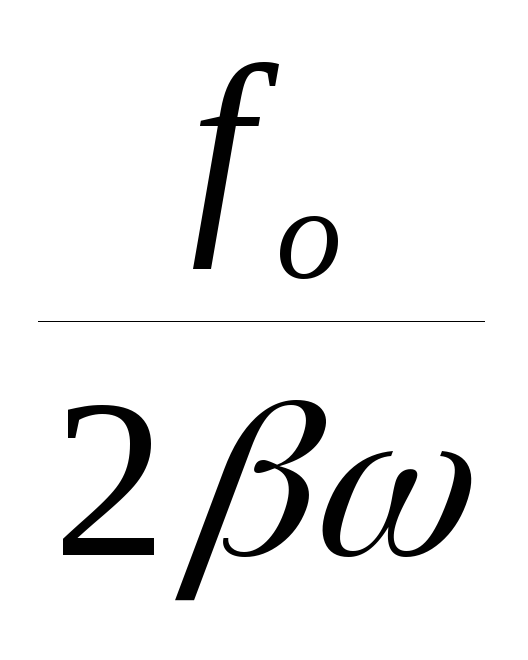
![]() ;
;
![]() -
ширина кривой
-
ширина кривой
![]() -
добротность характеризует меру ширины
резонансной кривой.
-
добротность характеризует меру ширины
резонансной кривой.
Импеданс (полное сопротивление колебательной системы)
Для колебательного контура можно ввести величину импеданса:
![]() =
R+i(wL-1/(wC))
Z=
=
R+i(wL-1/(wC))
Z=![]() =R+i(wL-1/(wC))
=R+i(wL-1/(wC))
![]()
1)
![]() –
связана с потерями энергии в контуре
–
связана с потерями энергии в контуре
2)
Im(![]() )=
wL-1/(wC
– реактивное сопротивление, связано с
запасами энергии.
)=
wL-1/(wC
– реактивное сопротивление, связано с
запасами энергии.
Величину импеданса можно ввести и для механической системы, например, пружинный маятник:
Z=r+i(wm-k/w)
18. Волновые процессы и их разновидности. Волновое уравнение. Плоские гармонические волны.
Под волнами понимают процессы распространения в пространстве возмущений вещества или поля, сопровождаемые переносом энергии, а иногда и информации.
Волны могут иметь разную физическую природу. Пример таких волн: электромагнитные и акустические.
По мере того как возмущения распространяются, можно выделить поверхность в пространстве (до точек этой поверхности дошло возмущение). Эта поверхность называется волновым фронтом. Геометрия фронта зависит от ряда факторов. Главными из них являются:
-
геометрия источника
-
спектральный состав возмущения
-
среда (её неоднородности)
Несколько видов волн:
1. Плоские волны

2 .
Сферические волны
.
Сферические волны
3. Цилиндрические волны

-
Упругие волны – распространяющиеся в упругой среде механические возмущения (деформации). Внешние тела, вызывающие эти возмущения в среде, называются источником волн. Распространение упругих волн состоит в возбуждении колебаний всё более и более удаленных от источника частиц среды. Важнейшее отличие упругих волн в среде от любого другого упорядоченного движения её частиц состоит в том, что при малых возмущениях (линейное приближение) распространение волн не связано с переносом вещества.
Упругая волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Упругая волна называется поперечной, если частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны.
Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т.е. способна сопротивляться деформации сдвига. Этим свойством обладают лишь твердые тела. Продольные волны связаны с объёмной деформацией среды. Поэтому они могут распространяться как в твердых телах, так и в жидких или газообразных средах. Исключением из этого правила являются поверхностные волны, образующиеся на свободной поверхности жидкости или на поверхности раздела несмешивающихся жидкостей. При этом частицы жидкости одновременно совершают продольные и поперечные колебания, описывая эллиптические или более сложные траектории.
Звуковые или акустические волны - распространяющиеся в упругой среде слабые возмущения – механические колебания с малыми амплитудами.
Волновое уравнение.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции , описывающей плоскую волну.
=Acos(wt-kx)
![]()
![]()
![]()
![]()
![]() одномерное
волновое уравнение.
одномерное
волновое уравнение.
Решением этого уравнения являются функции вида: =Acos(wt-kx), т.к. решение линейное, то линейные комбинации такой функции – тоже являются решением. Эти функции описывают распространение возмущений в пространстве.
![]()
В общем случае, когда нужно учесть три пространственных измерений, уравнение имеет вид:
![]()
Если есть система, распределенная в пространстве, её собственная динамика описывается таким уравнением, то в такой системе могут распространяться волны. Коэффициент стоящий в правой части уравнения характеризует квадрат фазовой скорости.
Плоские гармонические волны и их характеристики.
Фронт волны – плоскость, перпендикулярная направлению распространения волны.
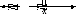
Пусть колебания листа происходят по закону косинуса. Смещение от положения равновесия =Acos(wt).
Вызовем плоскость, которая соответствует волновому фронту, на
расстоянии х от листа.
![]() t
– время запаздывания колебаний, V-
скорость распространения волны.
t
– время запаздывания колебаний, V-
скорость распространения волны.
=Acos(w(t-t )). Пусть потери энергии нет амплитуда и частота будут точно такие.
![]() ,
где k-
волновое число и
,
где k-
волновое число и
![]() .
.
![]() – уравнение
плоской волны.
– уравнение
плоской волны.
![]() радиус
вектор в любой точке волновой поверхности,
радиус
вектор в любой точке волновой поверхности,
![]() – волновой
вектор.
– волновой
вектор.
Y=Acos(wt-kx), где
-
=wt-kx – фаза зависит от t и x.
-
Y - смещение
-
А – амплитуда
-
w – циклическая частота.
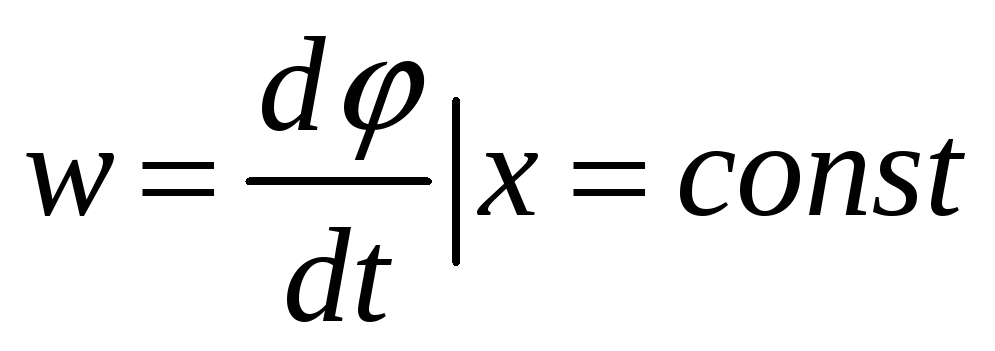 Показывает быстроту изменения фазы
колебаний в определенной точке
пространства. w=[c-1]
Показывает быстроту изменения фазы
колебаний в определенной точке
пространства. w=[c-1] -
- частота
-
T –период
-
к- волновое число.
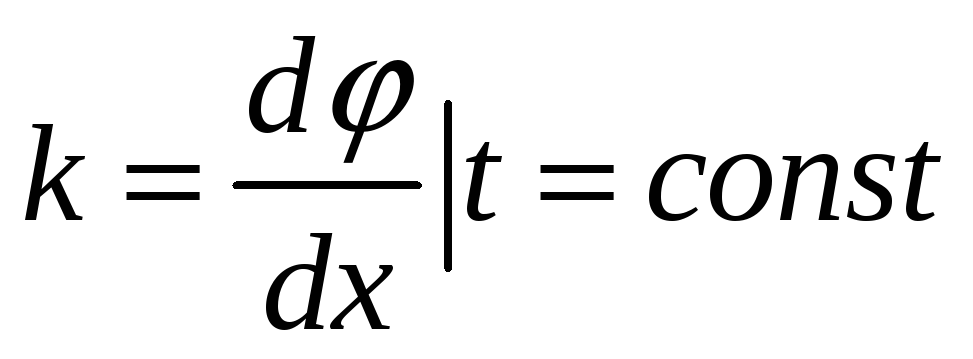 Показывает быстроту изменения фазы
колебаний в пространстве в фиксированный
момент времени.
Показывает быстроту изменения фазы
колебаний в пространстве в фиксированный
момент времени. -
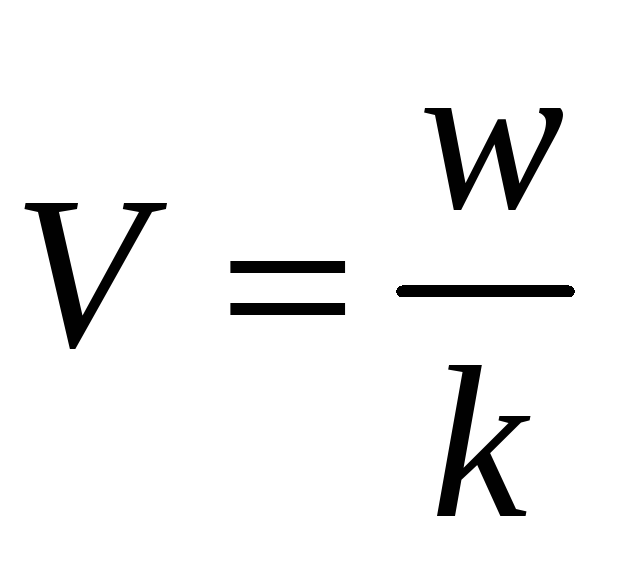 -
скорость волнового процесса.
-
скорость волнового процесса.
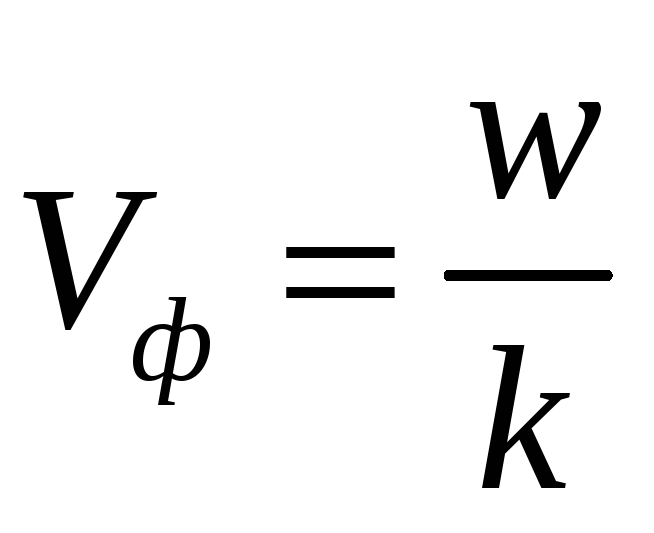 –фазовая скорость волны.
–фазовая скорость волны. -
- длина волны. k* =2 wT=2
- аналог Т, пространственный период волнового процесса.
l=
VфT
![]()
Уравнение волны можно представить в комплексном виде: Y=Аеi(wt-kx).
В общем случае jо!=0 , тогда Y=Acos(wt-kx+ jо), Y=Аeij еi(wt-kx).
19. Поперечные волны на непрерывной однородной струне. Волновое уравнение. Фазовая скорость волн. Импеданс струны.
Волновое уравнение для поперечных волн на струне.
![]()
-
упругость (возвращающее воздействие)
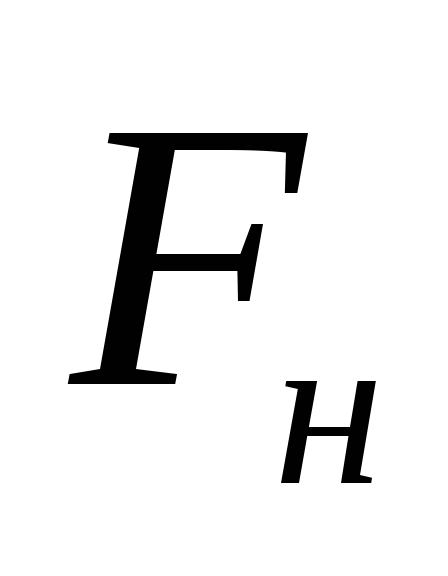
-
инертность

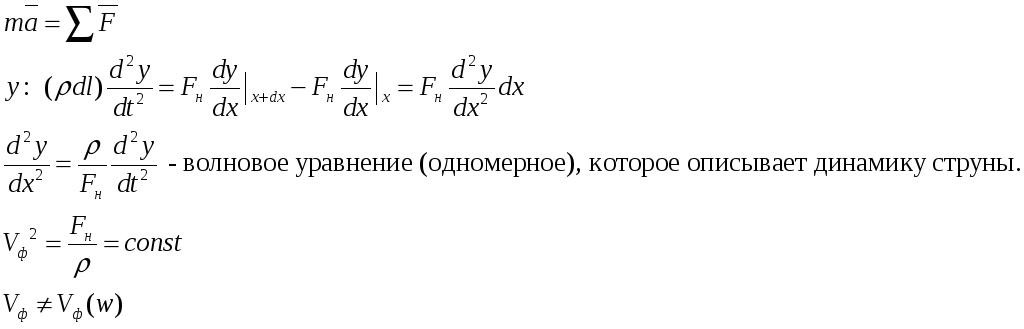 Поперечные
волны на непрерывной однородной струне
имеют дисперсии.
Поперечные
волны на непрерывной однородной струне
имеют дисперсии.
![]()
Импеданс струны. Гармонические волны на струне.
Возникает поперечная гармоническая волна:
![]()
![]()
-
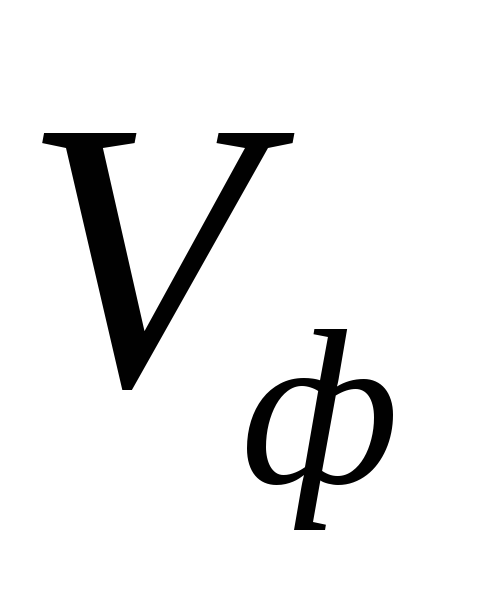 -
быстрота перемещения постоянной фазы.
-
быстрота перемещения постоянной фазы. -
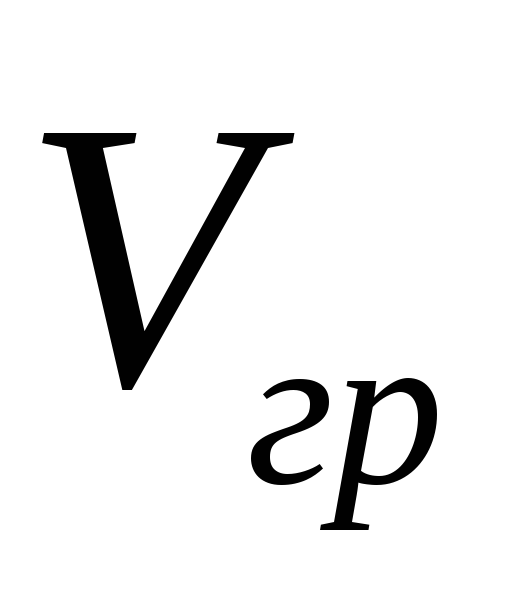 -
движение группы волн (энергии).
-
движение группы волн (энергии). -
 -
амплитуда колебаний скорости частиц
-
амплитуда колебаний скорости частиц
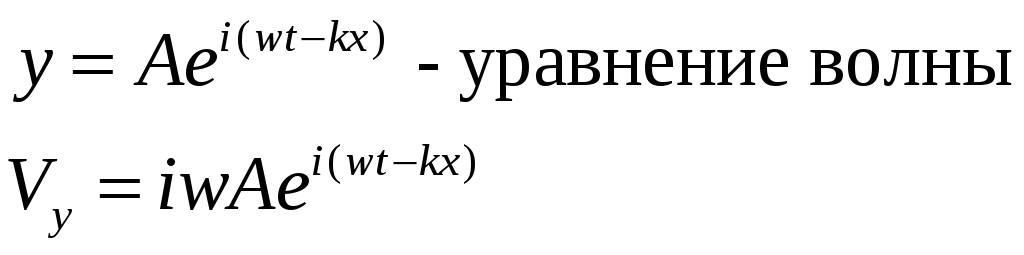
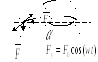
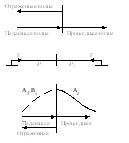
Внешнее воздействие можно связать с поперечной составляющей силы натяжения.
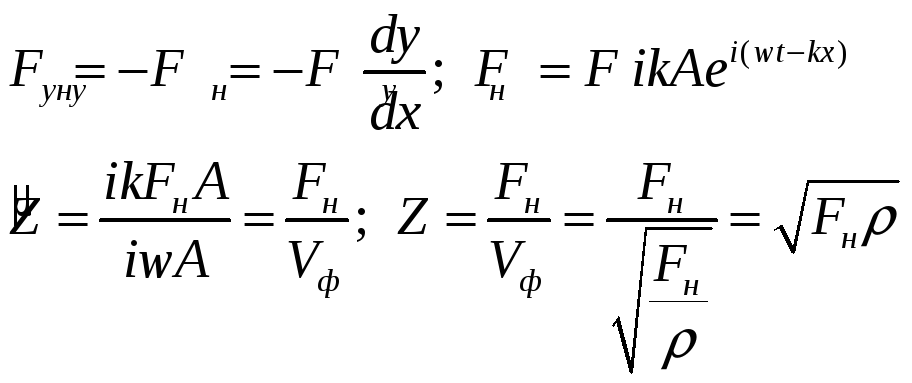
![]() -
импеданс
-
импеданс
Два
колебания в одной и той же фазе, т.к.
величина действительная
![]()
Источник
все время совершает работу. Источником
это воспринимается, как потеря энергии
(поэтому
![]() )
)
![]()
 ,
,
![]() ,
,
![]() ;
;
![]()
20. Поперечные волны на границе раздела струн. Стоячие волны на струне.
Поперечные волны на границе раздела двух струн.
На
границе раздела двух сред волны отражаются
и преломляются.
![]()
![]()
![]()
![]() :
:
![]() (1)
(1)
![]() (2)
(2)
![]()
 -
коэффициент прошедшей волны.
-
коэффициент прошедшей волны.
![]() -
коэффициент отраженной волны.
-
коэффициент отраженной волны.
Домножим (1) на k и вычтем из (1) (2)
![]()
![]() (3)
(3)
Домножим (1) на k и прибавим (1) к (2)
![]()
![]()
домножим
3 на
![]() =>
=>
![]() =>
=>
![]()
![]() =>
=>
![]()
1)
![]() =>
=>
![]()
2) ![]() =>
=>
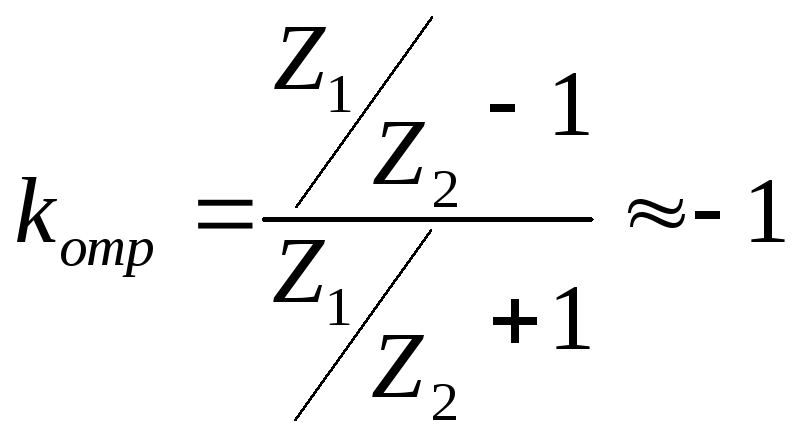
![]()
![]() Отраженная
волна имеет ту же амплитуду, что и
падающая. Волны будут
противофазными.
Отраженная
волна имеет ту же амплитуду, что и
падающая. Волны будут
противофазными.
3 )
)
![]() =>
=>
![]()
![]()
Стоячие волны на струне.
Это частный случай явления интерференции волн.
Интерференция волн – перераспределение энергии в пространстве связанное со сложением нескольких когерентных волн.
У когерентных волн одинаковые частоты колебаний и неменяющиеся со временем разности фаз.
Если по струне распространяется волна то результирующий волновой процесс есть сумма прямой и отраженной волны.
Е сли
сли
![]() - пряма волна то
- пряма волна то
![]() -
обратная волна.
-
обратная волна.
![]()
![]() -
уравнение стоячей волны для поперечных
волн на струне.
-
уравнение стоячей волны для поперечных
волн на струне.
Воспользуемся граничными условиями.
![]()
![]()
![]()
![]() -
условие существования стоячей волны.
-
условие существования стоячей волны.
Стоячие
волны могут существовать на струне <=>
когда на струне укладывается целое
число
![]() .
.
![]()
![]()
