19. Ортогональное планирование 2 - го порядка.

В окрестности оптимума линейного приближения уже не достаточно, доминирующими становятся коэффициенты регрессии, характеризующие элементы взаимодействия. Обычно окрестность экстремума, которую называют почти стационарной областью, удается описать полиномами 2-го порядка. Для этого нужно иметь такую систему планирования, в которой каждая из переменных будет принимать хотя бы 3 разных значения (количество уравнений у факторов как минимум равно 3). Такое планирование может быть получено путем добавления некоторого количества специально расположенных точек к «ядру», образованному планированием для линейного приближения. Такие планы называются композиционными, а само планирование центральным композиционным планированием. Рассмотрим случай: K = 2, N = 4 (при полном факторном эксперименте). Нужно получить:.

Для увеличения общего числа точек вводят так называемые «звездные точки».

ядро

звездные точки

центральная

всего 9 точек, следовательно необходимо

как минимум 9 опытов

В общем виде количество опытов . (ядро + звездные точки + центральная).

Рассмотрим трех – мерное производство:

К = 3 (= 27)

К = 4 (= 81)

Центральное композиционное планирование существенно уменьшает количество точек при увеличении К.

Необходимо создать новую матрицу планирования эксперимента, введя вместо изамену. При линейном приближении, когда мы использовали факторный эксперимент, мы получали ортогональное планирование и дисперсии для каждого коэффициента регрессии были минимальны и равны друг другу. При ортогональном планировании 2-го порядка мы будем пытаться добиться ортогональности в почти стационарной области. В общем случае матрица точек ЦКП не обеспечивает ортогональностью все векторы – столбцы, т.е.(*);(**)

Пример: Построим матрицу

+	+	+	+	+	+	+	+
+	+	+	-	+	-	+	+
+	+	-	+	-	+	+	+
+	-	+	+	-	-	+	+
+	+	-	-	-	-	+	+
+	-	+	-	-	+	+	+
+	-	-	+	+	-	+	+
+	-	-	-	+	+	+	+

Вместо квадратов введем переменную

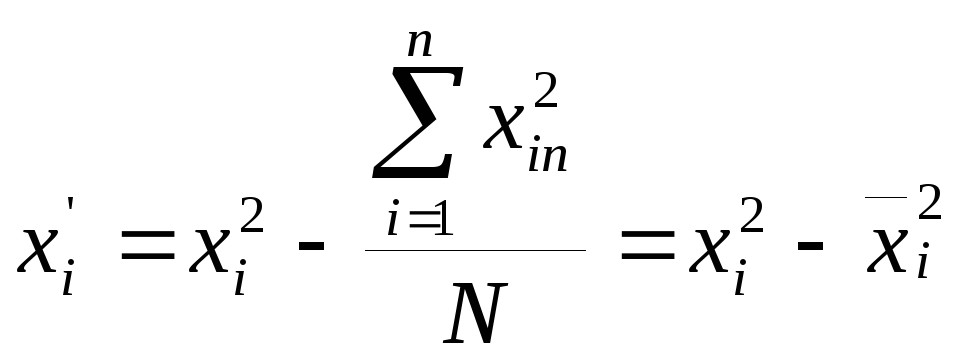
Нетрудно доказать, что будет зависеть только от числа переменных К.

	Число независимых переменных
	2	3	4
Ядро планирования
	1.000	1.215	1.414

Рассмотрим матрицу ортогонального планирования 2-го порядка для случая К = 3.

				-0,73	-0,73	-0,73
+	-	-	-	0,27	0,27	0,27	+	+	+		Ядро
+	+	-	-	0,27	0,27	0,27	-	-	+
+	-	+	-	0,27	0,27	0,27	-	+	-
+	-	-	+	0,27	0,27	0,27	+	-	-
+	-	+	+	0,27	0,27	0,27	-	-	+
+	+	-	+	0,27	0,27	0,27	-	+	-
+	+	+	-	0,27	0,27	0,27	+	-	-
+	+	+	+	0,27	0,27	0,27	+	+	+
+	-1,125	0	0	0,745	-0,73	-0,73	0	0	0		Звездные Точки
+	1,125	0	0	0,745	-0,73	-0,73	0	0	0
+	0	-1,125	0	-0,73	0,745	-0,73	0	0	0
+	0	1,125	0	-0,73	0,745	-0,73	0	0	0
+	0	0	-1,125	-0,73	-0,73	0,745	0	0	0
+	0	0	1,125	-0,73	-0,73	0,745	0	0	0
+	0	0	0	-0,73	-0,73	-0,73	0	0	0		Нулевая

(ядро), т.к.(для К = 3)

(звездные точки)

(начальная точка)

Проверим ортогональность:

(*)

(**)

Т.о. введя замену переменных, мы получаем ортогональную матрицу планирования эксперимента.

В результате, используя регрессионный анализ или метод наименьших квадратов, получим:

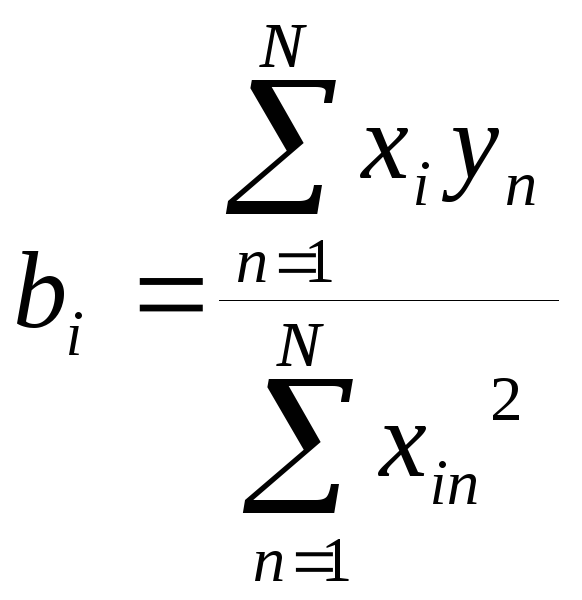
Чтобы определить оптимум, мы должны: . Получим,,и подставив их вполучим.