
- •Оглавление
- •Введение
- •1. Электростатика
- •1.1. Закон Кулона
- •1.2. Электрическое поле и его характеристики
- •1.3. Связь напряженности электрического поля и потенциала
- •1.4. Электрическое поле точечного заряда. Принцип суперпозиции
- •1.5. Графическое изображение электрических полей. Силовые линии и эквипотенциальные поверхности
- •1.6. Теорема Гаусса для электрического поля в вакууме
- •1.7. Проводники в электрическом поле
- •1.8. Электрическое поле в диэлектриках
- •1.9. Теорема Гаусса для электрического поля в диэлектриках
- •1.10. Конденсаторы
- •1.11. Энергия электрического поля
- •1.12. Потенциальность электрического поля. Теорема о циркуляции
- •2. Постоянный электрический ток
- •2.1. Закон Ома для однородного участка цепи
- •2.2. Работа и мощность электрического тока. Закон Джоуля - Ленца
- •2.3. Последовательное и параллельное соединение проводников
- •2.4. Источники тока. Закон Ома для полной цепи
- •2.5. Химические источники тока. Элемент Вольта
- •2.6. Закон Ома для неоднородного участка цепи
- •2.7. Правила Кирхгофа
- •Для лучшего уяснения всех нюансов, возникающих при применении правил Кирхгофа, рассмотрим пример достаточно разветвленной цепи.
- •2.8. Закон Ома в дифференциальной форме. Электронная теория проводимости
- •3. Магнетизм
- •3.1. Магнитное поле. Сила Лоренца
- •3.2. Движение заряженных частиц в электрических и магнитных полях
- •3.3. Сила Ампера
- •3.4. Рамка с током в магнитном поле
- •3.5. Эффект Холла
- •3.6. Вычисление магнитной индукции. Закон Био-Савара-Лапласа
- •3.7. Циркуляция и поток вектора магнитной индукции
- •3.8. Работа по перемещению контура с током в магнитном поле. Работа электродвигателя
- •3.9. Индуктивность
- •3.10. Закон электромагнитной индукции
- •3.11. Правило Ленца
- •3.12. Явления при замыкании и размыкании тока. Энергия магнитного поля
- •3.13. Генераторы и электродвигатели
- •3.14. Трансформаторы
- •3.15. Природа электромагнитной индукции
- •3.16. Магнитное поле в веществе
- •3.17. Теорема о циркуляции магнитного поля в веществе. Напряженность магнитного поля
- •3.18. Молекулярная теория магнетизма
- •3.19. Ток смещения. Уравнения Максвелла
- •3.20. Природа магнетизма
- •4. Электромагнитные колебания и волны
- •4.1. Колебательный контур
- •4.2. Колебательный контур с затуханием
- •4.3. Вынужденные колебания в lcr-контуре
- •4.4. Переменный ток в электрических цепях
- •4.4.1. Активное, индуктивное и емкостное сопротивления
- •4.4.2. Закон Ома для переменного тока. Активное и реактивное сопротивления
- •4.4.3. Метод векторных диаграмм
- •4.4.4. Эффективные напряжение и ток
- •4.4.5. Мощность в цепи переменного тока
- •4.5. Электромагнитные волны
- •4.5.1. Шкала электромагнитных волн
- •4.5.2. Получение электромагнитных волн
- •4.5.3. Энергия электромагнитных волн. Вектор Умова-Пойнтинга
- •Список литературы
4. Электромагнитные колебания и волны
4.1. Колебательный контур
Простейший пример электрических колебаний – это колебания напряжения и тока в обычной осветительной сети. Эти колебания происходят в результате действия внешней ЭДС генератора, изменяющейся по синусоидальному закону, т.е. являются вынужденными колебаниями. Напомним, что колебания можно разделить насвободныеивынужденные. Вынужденные колебания – это колебания, происходящие при воздействии на колебательную систему какой-либо внешнейпериодически действующей силы. Свободные колебания возникают при смещении колебательной системы из положения равновесия (т.е. внешняя сила действует только один раз перед началом колебаний) и в дальнейшем происходят без каких-либо внешних периодических воздействий на маятник. Простейшие примеры механических систем, совершающих свободные колебания – пружинный и физический маятники. А могут ли электрические величины совершать свободные колебания?
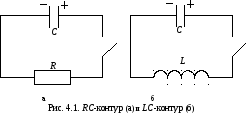
![]() конденсатор емкостью
конденсатор емкостью![]() замкнуть на резистор, то конденсатор
практически мгновенно разрядится (рис.
4.1,а). Энергия конденсатора по закону
сохранения не исчезает бесследно. При
протекании тока разрядки провод
нагреется, т.е. весь запас энергии
конденсатора перейдёт в тепло:
замкнуть на резистор, то конденсатор
практически мгновенно разрядится (рис.
4.1,а). Энергия конденсатора по закону
сохранения не исчезает бесследно. При
протекании тока разрядки провод
нагреется, т.е. весь запас энергии
конденсатора перейдёт в тепло:![]() .
Если же конденсатор замкнуть на катушку
с индуктивностью
.
Если же конденсатор замкнуть на катушку
с индуктивностью![]() (рис. 4.1, б), то конденсатор будет не просто
разряжаться, а перезаряжаться, т.е. в
контуре возникнут колебания заряда на
конденсаторе. А вместе с ними возникнут
и колебания тока в контуре, напряжения
на конденсаторе, ЭДС самоиндукции,
возникающей в витках катушки, колебания
энергий электрического поля конденсатора
и магнитного поля катушки. Энергия
электрического поля конденсатора будет
переходить в энергию магнитного поля
катушки, и наоборот
(рис. 4.1, б), то конденсатор будет не просто
разряжаться, а перезаряжаться, т.е. в
контуре возникнут колебания заряда на
конденсаторе. А вместе с ними возникнут
и колебания тока в контуре, напряжения
на конденсаторе, ЭДС самоиндукции,
возникающей в витках катушки, колебания
энергий электрического поля конденсатора
и магнитного поля катушки. Энергия
электрического поля конденсатора будет
переходить в энергию магнитного поля
катушки, и наоборот![]() .
Контур, состоящий из ёмкости и
индуктивности, называется колебательным
контуром без затухания (сопротивление
контура
.
Контур, состоящий из ёмкости и
индуктивности, называется колебательным
контуром без затухания (сопротивление
контура![]() )
илиLC-контуром. А сам
колебательный процесс вLC-контуре
называется электромагнитными колебаниями.
)
илиLC-контуром. А сам
колебательный процесс вLC-контуре
называется электромагнитными колебаниями.
Качественно
колебания в LC-контуре
можно объяснить следующим образом.
Главной причиной колебаний является
ЭДС самоиндукции![]() ,
возникающая в витках катушки при
изменении тока. После замыкания цепи в
контуре возникает электрический ток,
направленный от положительной обкладки
конденсатора к отрицательной. При этом
ЭДС самоиндукции препятствует нарастанию
тока, и он постепенно достигает своего
наибольшего значения к тому моменту,
когда конденсатор полностью разрядится.
Так как в этот момент движущая сила
(напряжение на конденсаторе) исчезла,
ток начинает уменьшаться. Но, опять-таки,
ток не может мгновенно уменьшится до
нуля, поскольку теперь в витках катушки
возникает ЭДС самоиндукции, препятствующая
убыванию тока, т.е. некоторое время
поддерживающая ток. За это время
конденсатор успевает перезарядиться.
,
возникающая в витках катушки при
изменении тока. После замыкания цепи в
контуре возникает электрический ток,
направленный от положительной обкладки
конденсатора к отрицательной. При этом
ЭДС самоиндукции препятствует нарастанию
тока, и он постепенно достигает своего
наибольшего значения к тому моменту,
когда конденсатор полностью разрядится.
Так как в этот момент движущая сила
(напряжение на конденсаторе) исчезла,
ток начинает уменьшаться. Но, опять-таки,
ток не может мгновенно уменьшится до
нуля, поскольку теперь в витках катушки
возникает ЭДС самоиндукции, препятствующая
убыванию тока, т.е. некоторое время
поддерживающая ток. За это время
конденсатор успевает перезарядиться.
Перед тем,
как рассмотреть вопрос о колебаниях в
LC-контуре количественно,
вспомним некоторые определения и выводы,
касающиеся гармонических колебаний и
изложенные в первой части физики –
механике. Колебания некоторой физической
величины![]() называются гармоническими, если она
изменяется со временем по закону косинуса
или синуса, т.е.:
называются гармоническими, если она
изменяется со временем по закону косинуса
или синуса, т.е.:
![]() ,
(4.1)
,
(4.1)
где
![]() амплитуда колебаний
(максимальное отклонение смещения
амплитуда колебаний
(максимальное отклонение смещения![]() от положения равновесия);
от положения равновесия);![]() циклическая частота
колебаний (
циклическая частота
колебаний (![]() период,
период,![]() частота колебаний);
частота колебаний);![]() фаза,
фаза,![]() начальная фаза
колебаний. Первая и вторая производные
величины
начальная фаза
колебаний. Первая и вторая производные
величины![]() по времени:
по времени:
![]() ,
,
![]() .
.
Из последнего
уравнения с учётом (4.1) следует
![]() или:
или:
![]() . (4.2)
. (4.2)
Соотношение (4.2) представляет собой дифференциальное уравнение гармонических колебаний.
Мы показали,
что если какая либо физическая величина
совершает гармонические колебания,
т.е. изменяется по закону (4.1), то для неё
справедливо дифференциальное уравнение
(4.2). В курсе дифференциальных уравнений
доказывается и обратное утверждение:
если для какой-либо физической величины
удалось (используя законы физики)
написать дифференциальное уравнение
(4.2), то единственным его решением будет
уравнение (4.1), т.е. величина
![]() совершает гармонические колебания.
При этом амплитуда
совершает гармонические колебания.
При этом амплитуда![]() и начальная фаза
и начальная фаза![]() определяются начальными условиями,
т.е. значениями величины
определяются начальными условиями,
т.е. значениями величины![]() и её первой производной
и её первой производной![]() в начальный момент времени
в начальный момент времени![]() .
Другими словами определяются тем, каким
образом экспериментатор «запустит
маятник».
.
Другими словами определяются тем, каким
образом экспериментатор «запустит
маятник».
Теперь
рассмотрим задачу о колебаниях в
LC-контуре. В контуре
действует единственная электродвижущая
сила – ЭДС самоиндукции![]() .
Согласно закону Ома для неоднородного
участка цепи, начало которого –
положительная обкладка конденсатора,
а конец – отрицательная (рис. 4.1,б), можно
записать:
.
Согласно закону Ома для неоднородного
участка цепи, начало которого –
положительная обкладка конденсатора,
а конец – отрицательная (рис. 4.1,б), можно
записать:![]() ,
где
,
где![]() разность потенциалов
или напряжение между обкладками
конденсатора. Так как сопротивление
контура
разность потенциалов
или напряжение между обкладками
конденсатора. Так как сопротивление
контура![]() ,
то:
,
то:
![]()
![]()
![]() .
.
По определению
сила тока – это заряд, протекающий через
сечение проводника за единицу времени,
т.е. производная заряда по времени (см.
формулу (2.1)). Если
![]() это заряд положительной
обкладки, то величина тока в контуре
это заряд положительной
обкладки, то величина тока в контуре![]() .
Знак минус учитывает тот факт, что после
замыкания ключа заряд положительной
обкладки убывает (
.
Знак минус учитывает тот факт, что после
замыкания ключа заряд положительной
обкладки убывает (![]() ).
Тогда производная тока по времени есть
вторая производная заряда по времени:
).
Тогда производная тока по времени есть
вторая производная заряда по времени:![]() .
В результате получим:
.
В результате получим:
![]()
![]()
![]() . (4.3)
. (4.3)
Отметим, что в электротехнике величина
ЭДС самоиндукции, взятая с обратным
знаком, рассматривается как напряжение
на катушке (индуктивности):
![]() .
Поэтому уравнение (4.3) можно записать в
виде
.
Поэтому уравнение (4.3) можно записать в
виде
![]() . (4.4)
. (4.4)
Уравнение (4.4) представляет собой, по сути, обобщение второго правила Кирхгофа, сформулированного нами ранее (см. п. 2.7) для замкнутых контуров с постоянными токами: сумма падений напряжений в замкнутом контуре равна алгебраической сумме внешнихЭДС, действующих в контуре. Внешние ЭДС вLC-контуре не действуют (ЭДС самоиндукции – это напряжение на индуктивности, внутренняя ЭДС).
Разделив обе
части уравнения (4.3) на величину
![]() ,
получим:
,
получим:
![]() . (4.5)
. (4.5)
Уравнение
(4.5) по форме совпадает с уравнением
(4.2), т.е. является дифференциальным
уравнением гармонических колебаний.
Роль физической величины
![]() играет заряд на обкладках конденсатора
играет заряд на обкладках конденсатора![]() .
Можно сделать два вывода: во-первых,
заряд на обкладках конденсатора изменяет
по гармоническому закону
.
Можно сделать два вывода: во-первых,
заряд на обкладках конденсатора изменяет
по гармоническому закону
![]() ; (4.6)
; (4.6)
во-вторых,
квадрат циклической частоты колебаний
(коэффициент при
![]() в уравнении (4.5)):
в уравнении (4.5)):![]() ,
откуда:
,
откуда:
![]() . (4.7)
. (4.7)
Период
колебаний связан с циклической частотой
![]() ,
тогда:
,
тогда:
![]() .
(4.8)
.
(4.8)
Формула (4.8) для периода колебаний заряда в LC-контуре называется формулой Томсона.
По гармоническому закону будут изменяться и другие физические величины, характеризующие процесс колебаний в LC-контуре. Зависимость напряжения на обкладках конденсатора от времени:
![]() ,
(4.9)
,
(4.9)
где
![]() максимальное
напряжение или амплитуда напряжения
на конденсаторе.
максимальное
напряжение или амплитуда напряжения
на конденсаторе.
Зависимость от времени силы тока найдется дифференцированием заряда по времени:
![]() , (4.10)
, (4.10)
где
![]() максимальный ток
в контуре или амплитуда тока.
Воспользовавшись известной формулой
тригонометрии
максимальный ток
в контуре или амплитуда тока.
Воспользовавшись известной формулой
тригонометрии![]() (формулой приведения), колебания тока
можно записать через функцию косинус:
(формулой приведения), колебания тока
можно записать через функцию косинус:
![]() .
.
![]() .
Это означает, что в тот момент, когда
заряд конденсатора и напряжение на нём
максимальны, т.е.
.
Это означает, что в тот момент, когда
заряд конденсатора и напряжение на нём
максимальны, т.е.![]() (напомним, что
(напомним, что![]() фаза), ток в контуре
равен нулю (если
фаза), ток в контуре
равен нулю (если![]() ,
то
,
то![]() ).
И, наоборот, когда ток максимален, заряд
и напряжение на конденсаторе равны
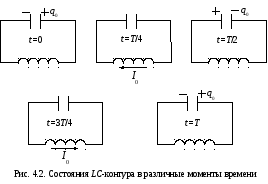
нулю. На рис. 4.2 показаны состоянияLC-контура в моменты
времени
).
И, наоборот, когда ток максимален, заряд
и напряжение на конденсаторе равны
нулю. На рис. 4.2 показаны состоянияLC-контура в моменты
времени![]() ,
где
,
где![]() период колебаний.
Предполагается, что в начальный момент
времени (
период колебаний.
Предполагается, что в начальный момент
времени (![]() )
заряд конденсатора максимален. Гармонические
колебания будут совершать также величины
ЭДС самоиндукции, энергий электрического
поля конденсатора и магнитного поля
катушки. Советуем читателям вывести
соответствующие выражения самостоятельно.
)
заряд конденсатора максимален. Гармонические
колебания будут совершать также величины
ЭДС самоиндукции, энергий электрического
поля конденсатора и магнитного поля
катушки. Советуем читателям вывести
соответствующие выражения самостоятельно.
Пример.
4.1. Максимальное значение напряжения
на обкладках конденсатораLC-контура![]() В. Определить значение силы тока
В. Определить значение силы тока![]() в контуре в тот момент, когда напряжение
на конденсаторе станет равным
в контуре в тот момент, когда напряжение
на конденсаторе станет равным![]() 5
В, если
5
В, если![]() нФ,
нФ,![]() Гн.
Гн.
Решение. Задачу можно решить, используя уравнения колебаний напряжения и тока (4.9) и (4.10). Однако проще воспользоваться законом сохранения энергии.
При колебаниях
в LC-контуре энергия
электрического поля конденсатора
переходит в энергию магнитного поля
катушки, и наоборот. Суммарная энергия
электрического поля конденсатора и
магнитного поля катушки в любой момент
времени остаётся неизменной:![]() .
.
В начальный
момент времени напряжение на конденсаторе
и его заряд максимальны. При этом сила
тока в цепи равна нулю (рис. 4.2) и полный
запас энергии контура состоит из энергии
электрического поля конденсатора:
![]() .
В промежутке времени между
.
В промежутке времени между![]() и
и![]() по цепи идёт ток, но конденсатор ещё
полностью не разрядился. Поэтому энергия
контура в конечный момент времени:
по цепи идёт ток, но конденсатор ещё
полностью не разрядился. Поэтому энергия
контура в конечный момент времени:![]() .
Таким образом
.
Таким образом
![]()
![]()
![]()
![]()
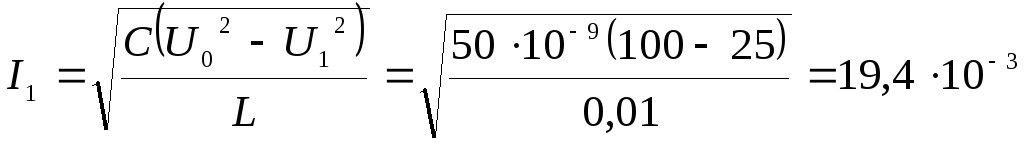 (А)
(А)![]() (мА).
(мА).
