3.4. Рамка с током в магнитном поле

На каждый элемент рамки с током, помещенной в магнитное поле, будет действовать сила Ампера. Суммируя все действия, можно определить результирующую силу Ампера и результирующий момент сил Ампера. Если магнитное поле однородно, то согласно выводу, сделанному в предыдущем параграфе, результирующая сила равна нулю, и на рамку будет действовать один только вращательный момент.

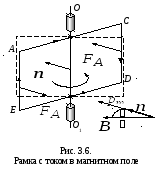
Рассмотрим рамку с током прямоугольной формы со сторонами и , помещенную в однородное магнитное поле с индукцией (рис. 3.6). Нормаль к плоскости рамки составляет с вектором магнитной индукции угол . На рис. 3.6 показаны силы Ампера, действующие на стороны рамки и . Силы, действующие на стороны и не создают вращательного момента относительно оси ОО₁. Предоставляем читателям самосто­я­тель­но определить направления дей­ствия этих сил (они будут растягивать рамку).

Моменты сил Ампера, действующих на стороны и :

, .

Суммарный вращательный момент, действующий на рамку:

.

Площадь рамки , тогда:

(3.8)

Введем характеристику рамки с током, называемую магнитным моментом рамки , направленным вдоль нормали и равным

. (3.9)

Направление нормали к плоскости рамки определяется направлением движения буравчика при вращении его по току.

Момент сил, действующих на рамку с током можно представить в виде:

(3.8,а)

Или в векторном виде:

(3.8,б)

Рамка будет находиться в равновесии, когда момент сил равен нулю. Это возможно, если или . В первом случае момент рамки параллелен вектору . Это устойчивое положение равновесия рамки (при небольших отклонениях рамка будет стремиться вернуться в положение равновесия). Во втором случае вектора и антипараллельны. Это неустойчивое положение равновесия (малейшее отклонение от этого положения приведет к развороту рамки на 180⁰).

Отметим, что полученные выражения (3.8,а) и (3.8,б) справедливы и для катушки с током (соленоида) во внешнем магнитном поле. В этом случае  магнитный момент катушки, где  число витков катушки.

Поведение рамки с током в магнитном поле аналогично поведению магнитной стрелки компаса. Магнитное поле ориентирует северный полюс стрелки вдоль направления вектора магнитной индукции . Это устойчивое положение равновесия стрелки. В случае рамки с током по направлению ориентируется магнитный момент (или нормаль к плоскости рамки ).

Если проводить параллели с электричеством, то свойства рамки с током во многом аналогичны свойствам электрического диполя (см. п. 1.8 и рис. 1.18 и 1.19). Напомним, что диполь – это система из двух точечных зарядов и , находящихся на расстоянии друг от друга. Дипольным моментом называется векторная величина . Вектор , а вместе с ним и , направлены от отрицательного заряда к положительному. Можно легко доказать, что на электрический диполь, находящийся в однородном электрическом поле с напряженностью , действует вращательный момент:

.

В устойчивом положении равновесия дипольный момент параллелен вектору , а в неустойчивом положении равновесия вектора и антипараллельны.

Аналогия между дипольным и магнитным моментом играет важную роль при описании диэлектрических и магнитных свойств вещества. При помещении диэлектрика в электрическое поле (см. п. 1.8) дипольные моменты молекул ориентируются в направлении поля. Этот процесс называется поляризацией диэлектрика и объясняет уменьшение напряженности электрического поля в диэлектрике по сравнению с полем в вакууме. Похожим образом происходит процесс намагничивания парамагнетиков, приводящий к усилению магнитного поля в веществе. Нужно немного воображения для того, чтобы молекулы или атомы рассматривать как маленькие рамки с токами. Токи создаются движением электронов вокруг ядер. Таким образом, молекулы и атомы могут обладать собственными магнитными моментами, которые ориентируются по внешнему магнитному полю. Этот процесс и есть намагничивание. Мы еще будем рассматривать его в п.п. 3.16 - 3.18.

В неоднородном магнитном поле на виток с током, помимо момента, будет действовать еще и результирующая сила. Приведем выражение для этой силы без вывода:

(3.9)

Предполагается, что ось направлена вдоль вектора .