2.6. Закон Ома для неоднородного участка цепи

Неоднородный участок цепи в отличие от однородного включает источник тока (рис. 2.12). На таком участке цепи на свободные заряды кроме сил электрического поля действуют сторонние силы. Значит, и работу на таком участке совершают как электрическое поле, так и источник тока. Результат работы всех сил, действующих на участке цепи с активным сопротивлением при прохождении тока, может быть единственным – нагревание сопро­тив­ления. Следовательно, для не­од­но­родного участка цепи

. (2.17)

Это уравнение полезно сравнить с аналогичным уравнением для однородного участка цепи , которое использовалось при выводе закона Джоуля-Ленца (2.6). В случае однородного участка работу совершает только электрическое поле.

Будем считать, что источник тока (рис. 2.12,а) разряжается, т.е. ток направлен от точки с потенциалом к точке с потенциалом. Пусть- заряд, прошедший по участку цепи. Тогда, а из определения ЭДС (см.(2.13)). Тепло выделяется как на внешнем сопротивлении, так и на внутреннем сопротивлении источника, поэтому по закону Джоуля-Ленца. Учитывая, что, из (2.17) получим:

.

Отсюда следует:

. (2.18)

Выражение (2.18) и представляет собой закон Ома для неоднородного участка цепи.

Вывод закона Ома для неоднородного участка в случае, когда источник тока заряжается, во многом аналогичен выводу, приведенному выше. В этом случае, очевидно, где-то в цепи есть иные источники, которые заряжают наш источник и обуславливают направление тока, показанное на рис. 2.12,б. Работа источника теперь будет отрицательной . Если химическая реакция в элементе обратима, то, пропуская ток в обратном направлении, заряжая источник, можно восстановить исходное состояние элемента, т.е. восстановить запасы его энергии. В прямой химической реакции при разрядке источника энергиявыделяется, а в обратной реакции точно такая же энергия поглощается источником. Если в первом случае источник совершает положительную работу, то во втором случае ее следует считать отрицательной.

Работа электрического поля теперь будет равна , так как положительный заряд переносится от точки с потенциаломк точке с потенциалом.

Записывая закон сохранения энергии, и выполняя простейшие преобразования, получим:

. (2.18,а)

Рассмотрим несколько частных случаев.

1. Исключим из участка цепи источник тока. Тогда 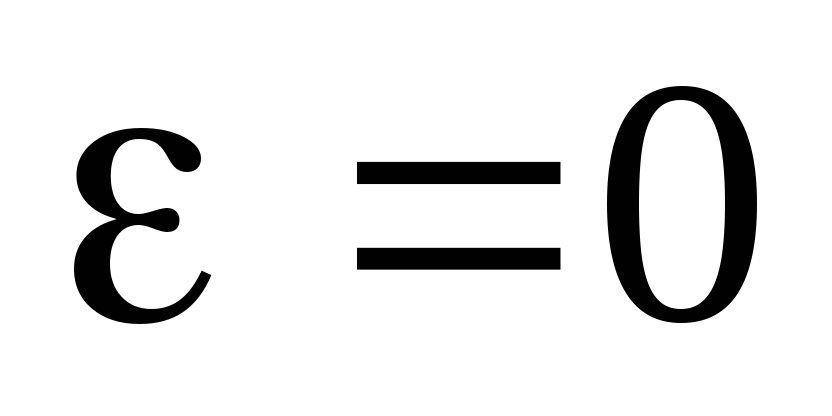,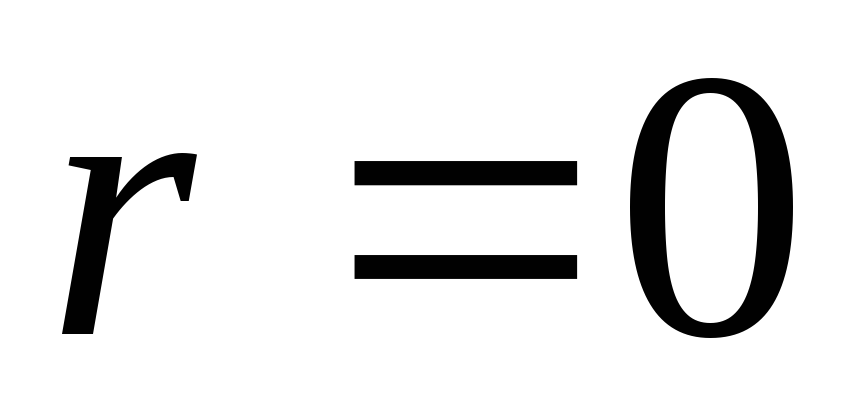и, как и следовало ожидать, из (2.18) получим закон Ома для однородного участка цепи:

.

2) Соединим (закоротим) точки 1 и 2, тогда , и мы получили замкнутую цепь (рис. 2.9). Из (2.18) закономерно следует закон Ома для замкнутой цепи:

.

3) Исключим из участка цепи внешнее сопротивление . Тогда в случае разрядки источника из (2.18,а) получим, что разность потенциалов на его клеммах:

(сравните с полученной ранее формулой (2.15)). При достаточно больших токах напряжение на клеммах источника может оказаться больше ЭДС.

В случае зарядки источника из (2.18,а) получим, что разность потенциалов на его клеммах:

В заключение подчеркнем, что закон Ома для неоднородного участка цепи является, по сути, прямым следствием закона сохранения энергии (и, конечно, закона Джоуля-Ленца).