2.3. Последовательное и параллельное соединение проводников

В практике электрические цепи представляют собой самые разные варианты соединения проводников, поэтому нужно уметь сложные цепи поэтапно сводить к двум важнейшим случаям: последовательномуипараллельномусоединению проводников. Законы параллельного и последовательного соединения проводников выводятся практически так же, как и законы параллельного и последовательного соединения конденсаторов (см. п.1. 10).

Рассмотрим участок цепи АВ, состоящий из трех последовательно соединенных проводников с сопротивлениями R₁, R₂ и R₃ (рис. 2.2). По всем проводникам течет один и тот же ток , где  суммарная сила тока, протекающего через участок АВ (т.е. ток, входящий в точку А и соответственно выходящий из точки В). Если бы это равенство было не верно, то количество заряда, втекшего за единицу времени, например, в первый провод было бы не равного количеству заряда вытекающему из него. Другими словами, в точках соприкосновения проводов накапливались бы заряды, что в стационарном случае невозможно. Полное напряжение на участке АВ равно сумме падений напряжений на каждом проводнике.

Общим сопротивлением участка цепи АВ назовем отношение напряжения на концах участка к полной силе тока, идущего по участку:.

Тогда из последних двух уравнений и закона Ома следует: . Учитывая равенство токов, получим:. Таким образом, в случае последовательного соединения проводников их общее сопротивление равно сумме сопротивлений:

. (2.8)

Теперь рассмотрим участок цепи АВ, состоящий из трех параллельно соединенных проводов (рис. 2.2). В этом случае общее падение напряжения на участке равно падению напряжения на каждом проводнике:. Действительно, все сопротивления подключены к одним и тем же точкамА и В и, следовательно, все их левые концы имеют потенциал , а правые концы . Общий ток, идущий по участку, в узлеА разделяется на три части, поэтому: . Используя последнее уравнение и закон Ома, определим общее сопротивлениеучастка цепиАВ:

.

Итак, в случае параллельного соединения проводников их общее сопротивление вычисляется по формуле:

. (2.9)

Предлагаем читателям самостоятельно обобщить формулы (2.8) и (2.9) на случай произвольного количества проводников.

Результаты (2.8) и (2.9) легко объяснить на примере двух одинаковых проводников с сопротивлением R. В случае последовательного соединения: , а в случае параллельного:. Действительно, последовательное соединение двух одинаковых проводников будет эквивалентно увеличению в 2 раза общей длины провода, а, следовательно, увеличению в 2 раза и общего сопротивления (см. (2.3)). Параллельное соединение двух одинаковых проводников эквивалентно увеличению в 2 раза площади сечения провода. В этом случае общее сопротивление уменьшится в 2 раза.

Пример 2.3. Найти сопротивление участка цепи АВ (рис. 2.3). Все сопротивления в схеме одинаковы и равны 8 Ом.

Решение. Последовательно, шаг за шагом, упрощаем исходную схему (рис.2.3). Заменим параллельно соединенные сопротивления R₂ и R₃, а также R₄ и R₅ на их результирующие сопротивления R₂₃ и R₄₅ и от схемы (а) перейдем к схеме (б). Согласно формуле (2.9):

Ом.

Точно так же получаем Ом. СопротивленияR₁ и R₂₃ схемы (б) соединены последовательно. По формуле (2.8) находим эквивалентное им сопротивление: (Ом) и переходим к схеме (в). Так как сопротивления схемы (в) соединены параллельно, эквивалентное им сопротивление определяется по формуле (2.9):

Ом.

Итак, мы нашли сопротивление участка цепи АВ, придя к простейшей схеме (г).

Пример 2.4. Определить общий ток в цепи и ток через сопротивление R₃ в схеме на рис. 2.3, если разность потенциалов между точками А и В В. Все сопротивления одинаковы и равны 8 Ом.

Решение. Прежде всего, нужно определить общее сопротивление участка цепи Ом (см. пример 2.3). Далее решение задачи сводится к последовательному расчету схем г, в, б, а.

Схема (г). По закону Ома находим ток через сопротивление R₀ (общий ток в цепи): (Ом).

Схема (в). Так как сопротивления R₁₂₃ и R₄₅ соединены параллельно, то В. Находим токи через эти сопротивления:А,А. Заметим, что токможно было определить и по-другому. Для параллельного соединения проводников имеем:А.

Схема (б). Через сопротивления R₁ и R₂₃ течет один и тот же ток, так как они соединены последовательно. Причем этот ток равен току через эквивалентное им сопротивление R₁₂₃ (который мы нашли, рассчитывая цепь (в)): А. Таким образом, мы можем рассчитать напряжение на сопротивленииR₂₃: В.

Схема (а). Так как сопротивления R₂ и R₃ соединены параллельно, то В (величинумы нашли, рассчитывая схему (б)). ТогдаА.

Токи и напряжения на оставшихся сопротивлениях рекомендуем рассчитать самостоятельно.

Пример 2.5. Найти сопротивление между точками А и В цепи, изображенной на рис. 2.4. ,,,.

Решение. Точки цепи 1 и 3 соединены проводом с пренебрежимо малым сопротивлением. Такое соединение точек цепи называется коротким замыканием. Падение напряжения на проводе с нулевым сопротивлением , откуда следует. Таким образом, потенциалы точек, замкнутых накоротко, совпадают.

Итак, сопротивления иподсоединены к точкам с одинаковыми потенциалами. Напряжения на этих сопротивлениях совпадают:(напряжение на первом сопротивлении, а на втором ). Следовательно, можно считать, что сопротивленияисоединены параллельно, и точку 1 соединить с точкой 3 (рис. 2.4). Отметим, что соединение точек с одинаковыми потенциалами является одним из принципов нахождения общего сопротивления участка цепи.

Используя вышесказанное, преобразуем цепь так, как показано на рис. 2.4. Легко определить, что . Сопротивленияисоединены последовательно и т. д. Конечный результат получить несложно:.

А как быть в случае более сложных схем, в которых невозможно найти ни одной пары сопротивлений, соединенных последовательно или параллельно? Или невозможно указать узлы с одинаковыми потенциалами, как мы это сделали в примере 2.5? Такая схема изображена на рис. 2.5. Здесь, например, сопротивления R₁ и R₄ нельзя считать соединенными последо­ва­тель­но, поскольку между ними есть узел С. В результате через эти сопротивления могут течь разные токи, так как в узле С ток делится на две части – токии. Или, например, сопротивленияR₁ и R₂ нельзя считать соединенными параллельно, поскольку их правые части соединены проводом с отличным от нуля сопротивлением R₃. В этом случае потенциалы точек С и D могут не совпадать (потенциал может падать на сопротивлении R₃), а значит и напряжение на сопротивлениях R₁ и R₂ может быть различным.

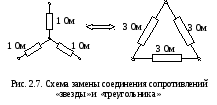
Наиболее универсальным методом для расчета сложных электрических цепей является применение правил Кирхгофа (см. п. 2.6). Здесь же мы покажем, как в некоторых случаях можно обойтись и без этих правил.

Замены последователь­но или параллельно сое­ди­нен­ных сопротивлений на эквивалентные по формулам (2.8) или (2.9) являются простейшими примерами пре­­образования электри­чес­ких цепей с двумя выводами. Теперь посмотрим, как «пре­об­разуются» друг в друга схе­мы, имеющие три вывода,  «звезда» и «треугольник» (рис. 2.6). На рис. 2.6 для удобства сопротивления схемы (а) обозначены малыми буквами, а сопротивления схемы (б) – большими с двойным индексом. Например, сопротивление R₂₃ включено между выводами 2 и 3 и т. д. Если мы хотим заменить одну схему другой, наша задача – получить такие соотношения между r и R, чтобы сопротивления между любыми двумя точками были для обеих схем одинаковыми.

Для того, чтобы найти сопротивление, например, между точками 1 и 2, нужно подать разность потенциалов на эти точки. Тогда в схеме «звезда» ток через сопро­тив­ление r₃ не пой­дет и сопротивления r₁ и r₂ соединены последо­ва­тель­но, поэтому сопротивление между точками 1 и 2 равно . В схеме «треу­голь­ник» сопротивление между точ­ками 1 и 2

,

(сопротивления R₁₃ и R₂₃ будут соединены последовательно, а их общее сопротивление и сопротивлениеR₁₂ будут соединены параллельно). Для того чтобы сопротивления между точками 1 и 2 были одинаковыми в обеих схемах, необходимо, чтобы

.

Аналогичные выражения можно получить для точек 1 и 3, 2 и 3:

, .

Решая систему из трех полученных уравнений, получим формулы для прямого:

(2.10)

и для обратного преобразования:

(2.11)

Пользуясь формулами (2.10) и (2.11), можно производить замену одной схемы другой. Например, «звезду с сопротивлениями 1 Ом можно заменить «треугольником» с сопротив­лениями 3 Ом (рис. 2.7).

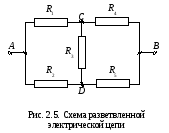
Пример 2.6. В схеме на рис. 2.5 Ом,Ом. Определить: 1) сопротивление участка цепиАВ, 2) ток через сопротивление , если точкиА и В подключены к напряжению В.

Решение. На рис. 2.8 показана последовательность преобразований схемы. Отметим лишь, что самым первым было преобразование «треугольника» ACD в «звезду». При этом мы воспользовались формулами (2.10) (см. также рис. 2.7). Для общего сопротивления участка АВ получаем Ом.

Для нахождения общего сопротивления участка можно было выбрать несколько вариантов преобразования исходной схемы. Например, можно было сначала «треугольник» CBD превратить в «звезду» или, наоборот, «звезду» с центром в узле С (или D) превратить в треугольник. Однако, помимо общего сопротивления, нам необходимо найти еще и ток через сопротивление R₅. Поэтому схему нужно преобразовать так, чтобы не затронуть интересующее нас сопротивление R₅. Этим мы и руководствовались при выборе преобразований.

Рассматривая упрощенные схемы, также как и в примере 2.4, легко получить, что общий ток, поступающий на участок цепи АВ А, а ток через сопротивлениеR₅: А.