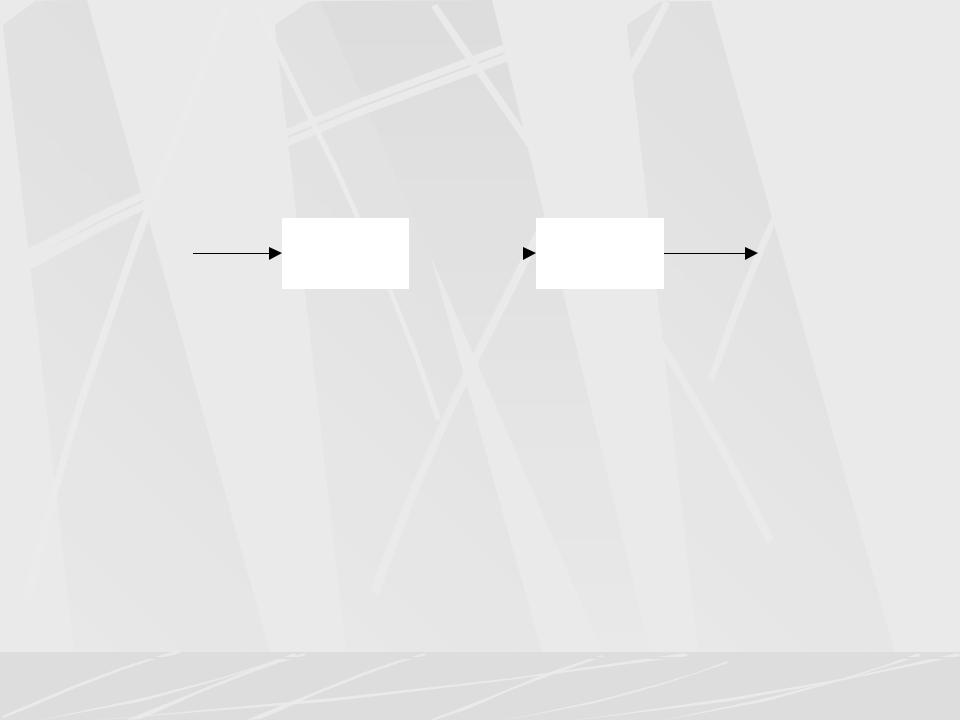
Но такая запись, соответствует последовательному соединению фильтров с передаточными функциями H1 (z) и H2 (z) . На рисунке показано последовательное соединение двух фильтров.
x(n) |
|
v(n) |
|
y(n) |
||
H2 (z) |
H1 (z) |
|||||
|
|
|
|
|||
|
|
|
|
|
|
|
Для этих фильтров напишем соответствующие им разностные уравнения. У первого фильтра все коэффициенты am 0 . Поэтому из общего разностного уравнения (87) находим уравнение для первого фильтра.
N |
|
y(n) bk v(n k) |
(95) |
|
|
k 0 |
|
61
У второго фильтра b0 1 , а все остальные коэффициенты bk 0 . Поэтому из общего разностного уравнения (87) находим уравнение для второго фильтра.
M
v(n) x(n) am v(n m) (96)
m 1
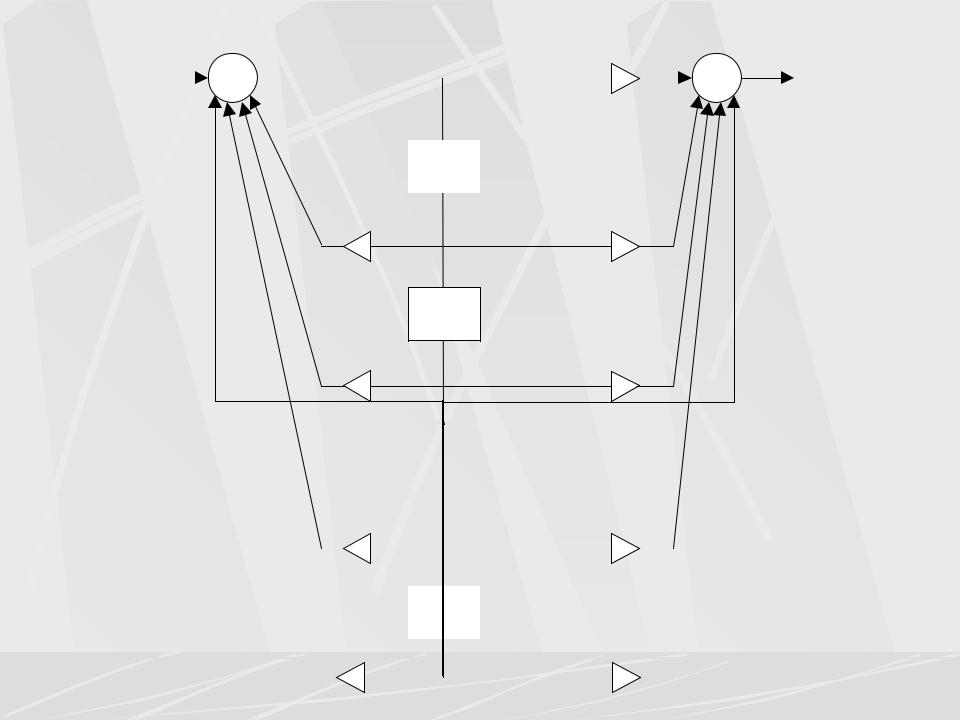
Структурная схема, соответствующая уравнениям (95), (96) показана на следующем рисунке.
Здесь число L определяется по формуле:
L max(N, M )
62
x(n) |
|
v(n) |
b0 |
|
|
|
|
y(n) |
||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
z 1 |
|
b1 |
|
v(n) |
||||
1 |
|
|||
a2 |
z 1 |
b2 |
v(n) |
|
aL 1 |
v(n L 1) |
bL 1 |
|||
|
|
|
||||
|
|
|
|
|
|
|
|
aL |
z 1 |
|
|
b |
|
v(n |
L) |
|||||
|
|
L |
||||
|
|
|
|
|
||
63
Пример 9. Построить прямую каноническую форму структурной формы фильтра из примера 8.
В примере 8 коэффициенты фильтра равны.
b0 1, b1 3, b2 2, a1 0.4
Это означает, что уравнения (95), (96) для этого фильтра имеют вид.
y(n) v(n) 3v(n 1) 2v(n 2)
v(n) x(n) |
0.4v(n 1) |
(97) |
|
64
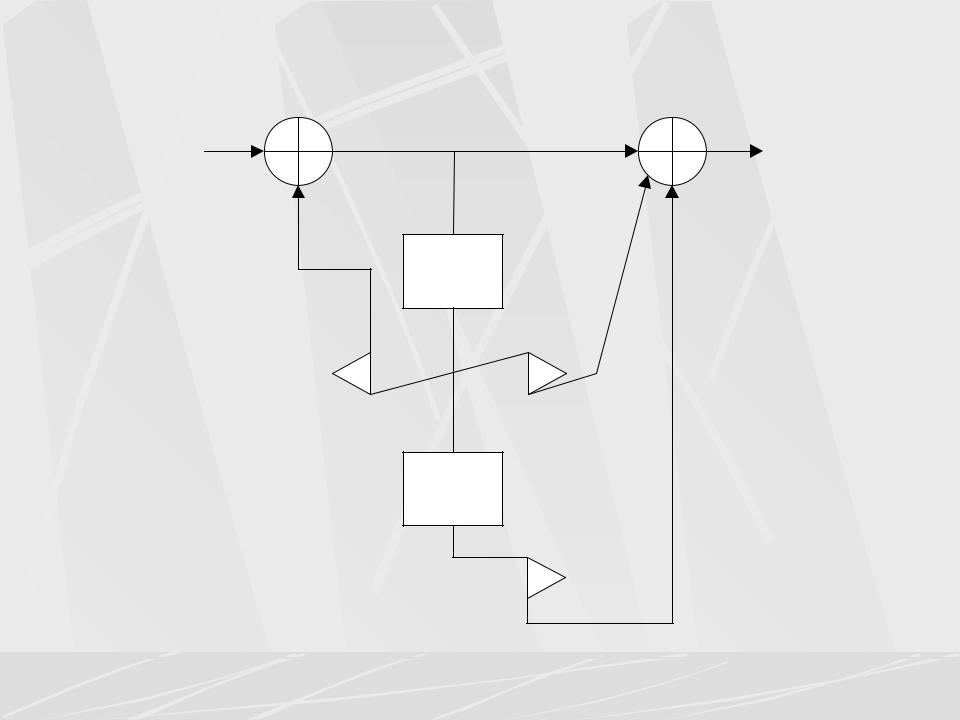
На рисунке показана каноническая форма, соответствующая |
уравнениям (97). |
z 1 |
3 |
z 1 |
2 |
Здесь число L =2 , и число элементов задержки тоже равно двум. |
65 |
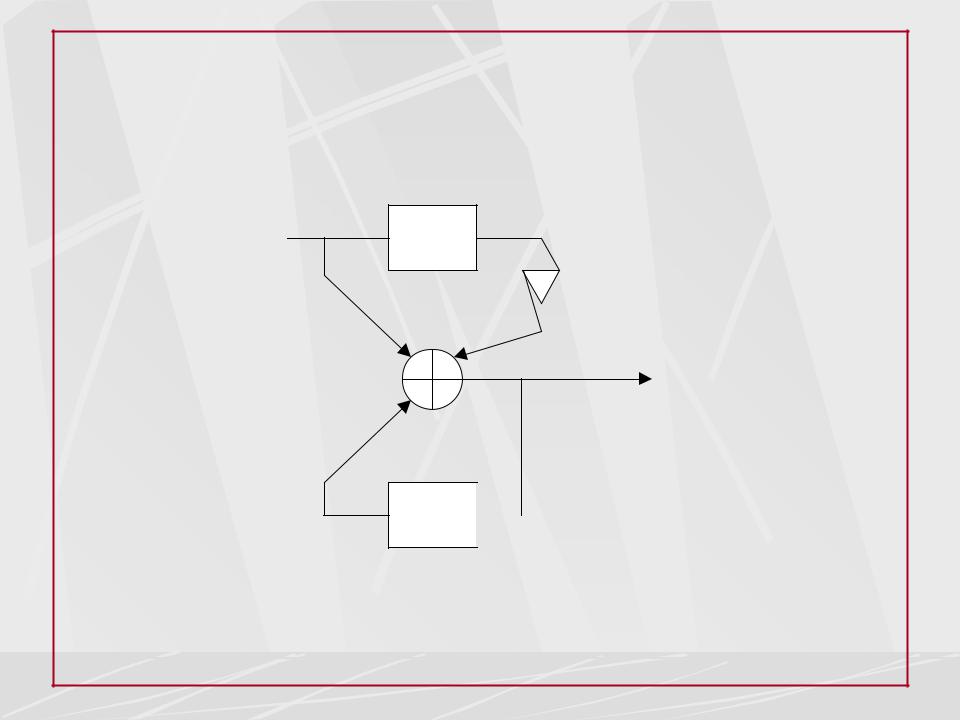
Пример 10. Найти передаточную функцию, импульсную характеристику и упростить структурную схему фильтра, изображенного на рисунке.
z 1
1
z 1 
Убедитесь самостоятельно, что Н(z)=1,
h(n) ~(n).
66
Доказать, что для системы с квадратичной нелинейностью выполняется соотношение:
x1(t) x2 (t) y1(t) y2 (t) 2x1(t)x2 (t)
x(t) y(t) x2 (t)
x1(t) y1(t) x12 (t) x2 (t) y2 (t) x22 (t)
x(t) x1(t) x2 (t) y(t) (x1(t) x2 (t))2x12 (t) 2x1 (t)x2 (t) x22 (t)
y1(t) 2x1(t)x2 (t) y2 (t) 
67