
Лекции / Лекции (Павлова) / L30
.docЛекция №30.
![]() Запишем
условия направленности химического
процесса. При p
и Т, имеем
Запишем
условия направленности химического
процесса. При p
и Т, имеем
в![]() самопроизвольном процессе
имеем для самопроизвольного процесса
самопроизвольном процессе
имеем для самопроизвольного процесса
т.е. изменение этой функции определяет знак.
Пример.
Раскроем условие химического равновесия для каждого участника реакции. Предположим у нас: гомогенная, газообразная фаза.
Раскроем химический потенциал
i=io(T)+RTlnpi. (io(T) – константа интегрирования).
П![]() одставим
эти выражения в наши уравнение и
сгруппируем члены:
одставим
эти выражения в наши уравнение и
сгруппируем члены:
В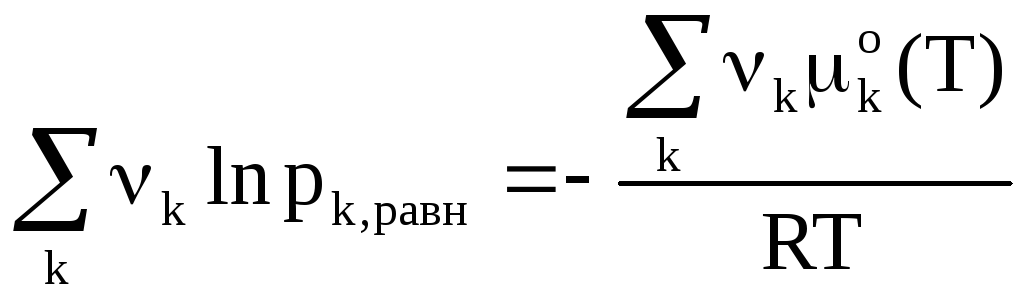 ведем
условие, что это равенство определяет
химическое равновесие.
ведем
условие, что это равенство определяет
химическое равновесие.
М ожно
представить правую часть в другом виде
ожно
представить правую часть в другом виде
Правая часть зависит только от температуры и не зависит от излишнего давления и парциальных давлений в исходной смеси.
 Введем
обозначение:
Введем
обозначение:
С![]() учетом последнего равенства, с учетом
потенцирования получим:
учетом последнего равенства, с учетом
потенцирования получим:
Р аскроем
это выражение для нашей реакции:
аскроем
это выражение для нашей реакции:
Итак, в этом уравнение в числителе стоят произведения равные парциальных давлений, возведенные в степени стехиометрических коэффициентов.
 Данное
выражение называется знаком действующих
масс. Константа kр
– константа химического равновесия.
Индекс р внизу указывает, что kр
зависит
только от температуры. Независимость
kр
от давления
означает, что с изменением давления в
системе, парциальные давление реагируемых
веществ изменяется таким образом, что
величина kр
остается постоянной. Используя другие
выражения концентрации, закон действующих
масс можно представить в следующем
виде:
Данное
выражение называется знаком действующих
масс. Константа kр
– константа химического равновесия.
Индекс р внизу указывает, что kр
зависит
только от температуры. Независимость
kр
от давления
означает, что с изменением давления в
системе, парциальные давление реагируемых
веществ изменяется таким образом, что
величина kр
остается постоянной. Используя другие
выражения концентрации, закон действующих
масс можно представить в следующем
виде:
С – мольно-объемная концепция
![]() x
– мольная доля;
x
– мольная доля;
Фугитивность – вместо парциальных давлений. Иначе, рассеивание, летучести.
Фугитивность – эффективное давление.
 р
- парциальные давления
р
- парциальные давления
- коэффициент фугитивности
Если р0 в этом случае i=pi. Т.о. для реальных газов, константа равновесия:
А![]()
![]() налогично
в неидеальных растворах используется
активность
налогично
в неидеальных растворах используется
активность
х - мольная доля
![]() -
коэффициент активности
-
коэффициент активности
В![]() общем случае константа равновесия –
это размерная величина. Например, для
нашей реакции, размерность константы
равновесия определяется тем, как
соотносятся между собой стехиометрические
коэффициенты
общем случае константа равновесия –
это размерная величина. Например, для
нашей реакции, размерность константы
равновесия определяется тем, как
соотносятся между собой стехиометрические
коэффициенты
Пример:
3H2+N2=2NH3
kp=p-2
– константа
прямой реакции
О – обратный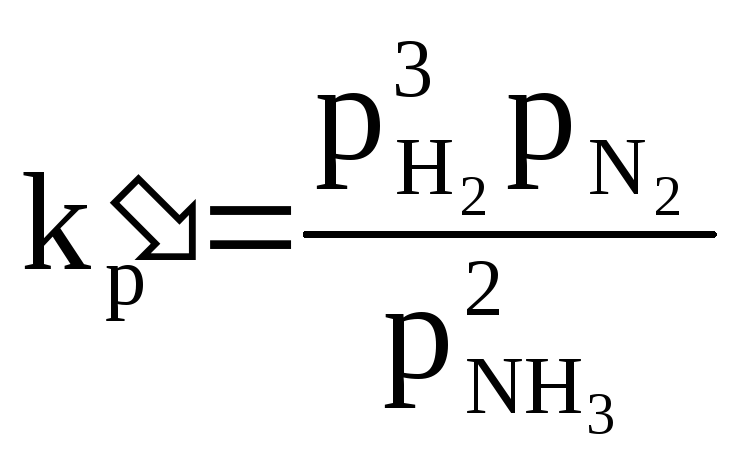
П![]() ри
записи химического уравнения можно в
одинаковое число раз менять стехиометрические
коэффициенты. Например, в нашей реакции
все коэффициенты можно уменьшить в 2
раза.
ри
записи химического уравнения можно в
одинаковое число раз менять стехиометрические
коэффициенты. Например, в нашей реакции
все коэффициенты можно уменьшить в 2
раза.
В зависимости от формы записи величина константы равновесия будет иметь разные числовые значения. Это надо иметь ввиду и при записи закона действующих масс нужно писать его либо в полном виде, либо писать рядом химическое уравнение.
Взаимосвязь между различными константами равновесия.
Н![]() айдем
связь между kp
и kC,
гомогенной реакции, протекающей в
газообразной фазе. Воспользуемся
уравнением Клайперона-Менделеева:
айдем
связь между kp
и kC,
гомогенной реакции, протекающей в
газообразной фазе. Воспользуемся
уравнением Клайперона-Менделеева:
Н

pi=ciRT
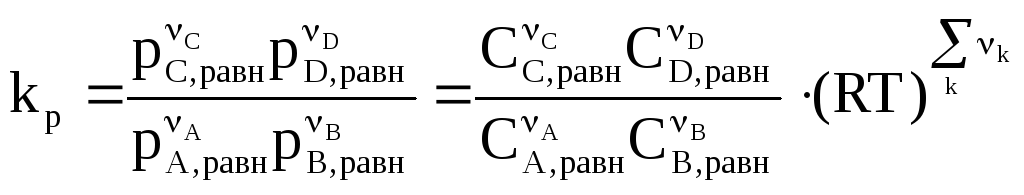 о
по определению мольной объемной
концентрации:
о
по определению мольной объемной
концентрации:
kp – не является функцией давления. Из этого следует, что и kC для идеальных газов также не является функцией давления. kC(p).
Аналогичным образом можно установить взаимосвязь между другими константами, например между kp и kC. Для этого воспользуемся уравнением Дальтона:
pi=pобщ*x1.
И![]()
![]() спользуя
это соотношение получим:
спользуя
это соотношение получим:
Вывод: поскольку kр(p), то из этого выражения следует, что kx – зависит от давления в общем случае.
Из представленных выражений вытекает, что для реакций, которые проходят без изменений числа молей имеет место равенство:
kp=kx=kC.
В этом случае величина константы является безразмерной величиной. В реальных системах, в случае широкого интервала изменяется давление и концентрации для реагируемых веществ, закон действующих масс нарушается, т.к. в газообразных, жидких и твердых системах, не является идеальными, всегда существует взаимодействие между молекулами. Поэтому и давление и концентрации не выражают действующих масс и константа равновесия не сохраняет постоянное значение. Обычно интервал изменения давлений, в котором еще можно пользоваться парциальным давлениями, а не фугитивными , не превышает 30-50 атм. Для ионных растворов трудно определить предел в котором соблюдается постоянство константы равновесия. Можно только отметить, что для растворов не электролитов, интервал в котором константы постоянны являются более широким. Эти отклонения связаны со сложными взаимосвязями в растворах между молекулами растворенного вещества и среднего растворителя.
Уравнение изотермы химической реакции.
![]() Обратимся
к уравнению, которое определяет изменение
энергии Гиббса в системе в которой
протекает химическая реакция. При
p,ξ=const.
Обратимся
к уравнению, которое определяет изменение
энергии Гиббса в системе в которой
протекает химическая реакция. При
p,ξ=const.
 Возьмем
достаточно большой объем реагирующей
смеси, такой чтобы при протекании одного
пробега реакции химические потенциалы
участников реакции не претерпели
изменения. Это условие позволяет нам
проинтегрировать это уравнение в
пределах.
Возьмем
достаточно большой объем реагирующей
смеси, такой чтобы при протекании одного
пробега реакции химические потенциалы
участников реакции не претерпели
изменения. Это условие позволяет нам
проинтегрировать это уравнение в
пределах.
В![]() ыразим
химические потенциалы через парциальные
уравнения:
ыразим
химические потенциалы через парциальные
уравнения:
![]()
К ак
и при выводе знака действующих масс,
обозначим величину
ак
и при выводе знака действующих масс,
обозначим величину
И![]() спользуем
это выражение, сделаем подстановку в
∆G.
спользуем
это выражение, сделаем подстановку в
∆G.
П рименим
это уравнение к заданной ранее реакции
рименим
это уравнение к заданной ранее реакции
 Последнее
выражение представляет собой уравнение
изотермы химической реакции. Это
уравнение определяет изменение энергии
Гиббса, при химической реакции в
результате которой А
молей вещества А, взятого при давлении
р’А
и В
молей вещества В, взятого при давлении
р’В,
переходит в С
молей вещества С, взятого при давлении
р’С
и D
молей D,
взятого при р’D.
Аналогичное уравнение можно записать
и для реакции, которая протекает при
постоянной температуре и объеме. В этом
случае вместо энергии Гиббса следует
использовать энергию Гельмгольца, а
закон действующих масс в этом случае
следует выразить через мольно-объемные
концентрации.
Последнее
выражение представляет собой уравнение
изотермы химической реакции. Это
уравнение определяет изменение энергии
Гиббса, при химической реакции в
результате которой А
молей вещества А, взятого при давлении
р’А
и В
молей вещества В, взятого при давлении
р’В,
переходит в С
молей вещества С, взятого при давлении
р’С
и D
молей D,
взятого при р’D.
Аналогичное уравнение можно записать
и для реакции, которая протекает при
постоянной температуре и объеме. В этом
случае вместо энергии Гиббса следует
использовать энергию Гельмгольца, а
закон действующих масс в этом случае
следует выразить через мольно-объемные
концентрации.
