Критерий Михайлова

Это частотный критерий, позволяющий судить об устойчивости замкнутой или разомкнутой системы по поведению её характеристического вектора на комплексной плоскости.

Критерий Михайлова является графоаналитическим методом оценки устойчивости с помощью годографа Михайлова характеристического вектора.

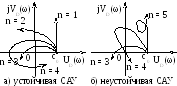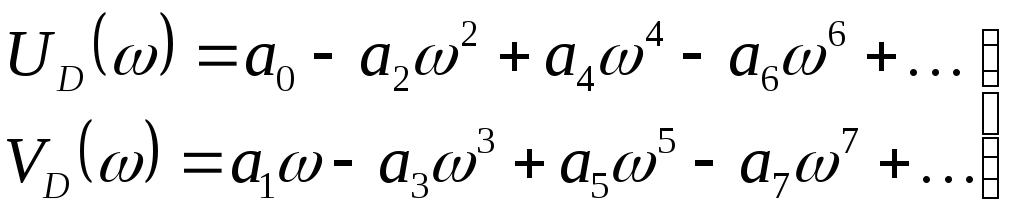Подставив в характеристический полином (4.5) вместоλ переменную jω, получим комплексную функцию: D(jω) = a_n(jω)ⁿ + a_n-1(jω)^n-1 + … + a₁(jω) + a₀ (4.12). После возведения в соответствующие степени, выражение (4.10) можно разбить на вещественную и мнимую части: D(jω) = U_D(ω) + jV_D(ω) (4.13), где (4.14)

Далее задав дискретные значения ω от 0 до ∞ можно вычислить соответствующие им значения U_D(ω) и V_D(ω) и по ним на комплексной плоскости построить годограф Михайлова.

Рис. 4.26. Графоаналитический критерий Михайлова (годограф Михайлова)

Представив выражение (4.13) в виде D(jω) = D(ω)e^jφ(ω) можно построить в полярных координатах годограф Михайлова, который начертит своим концом вектор, изменяясь по модулю и направлению с изменением частоты.

1. Структурные схемы и формулы САУ.

Преобразование структурных схем

ДЗ – динамическое звено,

ПФ – передаточная функция.

Структурная схема – представление САУ в виде совокупности ДЗ.

Рис.2.27. Структурная схема САУ

В прямоугольных блоках – ПФ блоков САУ, состоящие из элементарных ДЗ. Стрелками обозначаются связи между элементами и воздействия: выходное Y, задающее X, возмущающее f. Разветвления сигналов (узлы) обозначаются точками. Сумматоры – . Сумматор 1 вычисляет сигнал рассогласования ε = x – z.

Структурная схема представляет собой математическую модель САУ, состоящую из типовых ДЗ и являющуюся очень удобным, информативным и наглядным представлением САУ.

Для анализа и синтеза САУ необходимо на практике знать математическое описание системы в виде её общей ПФ.

Структурная схема позволяет просто решить эту задачу сворачиванием всей совокупности типовых ДЗ в одно. Для этого применяется 3 правила преобразования структурной схемы и правило переноса узла и сумматора.

Звенья в структурных схемах могут соединяться между собой последовательно, параллельно и встречно на схеме с обратной связью.

Рис.2.28. Структурные схемы соединений звеньев в САУ

1. ПФ цепочки последовательно соединённых звеньев равна произведению их ПФ: . (2.37)

2. ПФ группы параллельно соединённых звеньев равна сумме ПФ: .

3. ПФ группы звеньев, соединённых по схеме с обратной связью, равна отношению ПФ прямой цепи к выражению: 1 “­–” для положительной обратной связи и 1 “+”1 для отрицательной ПФ разомкнутой цепи:(ПФ замкнутой цепи) (2.39).

При положительной обратной связи сигнал обратной связи прибавляется к задающему воздействию, при отрицательной – вычитается из него.

Прямая цепь – совокупность звеньев, передающих сигнал от входа к выходу.

ПФ разомкнутой цепи состоит из ПФ цепи и ПФ обратной связи. В случае одноконтурной САУ ПФ такой цепи равна произведению ПФ всех звеньев.

Р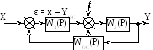ис.2.29. Правило переноса сумматора Рис.2.30. Правило переноса узла

Рис. 2.31. Одноконтурная линейная САУ с ПФ по возмущению, управлению и ошибке

Правило перевода / переноса сумматора и узла.

Определим ПФ по управлению, по возмущению и по ошибке для одноконтурной линии САУ. На основании принципа суперпозиции определим поочерёдно ПФ САУ по входу X и f, считая действующим только 1 из входов. Предполагая ,что f=0,определяем ПФ: (2.40). Аналогично ПФ по возмущению (X=0): . (2.41)

П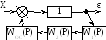Ф по ошибкеε получим после преобразования исходной схемы САУ в вид (f = 0,X = 0).

Рис. 2.32. Структурная схема САУ с ПФ по ошибкеε

ПФ прямой цепи между входным воздействием и сигналом ошибки равна 1, тогда ПФ САУ по ошибке: (2.42).

Анализируя ПФ (2.40-2.42) для случая, когда на линейную систему подаётся несколько воздействий z, на основании суперпозиции можно определить зависимость выходного сигнала от совокупности входящих: 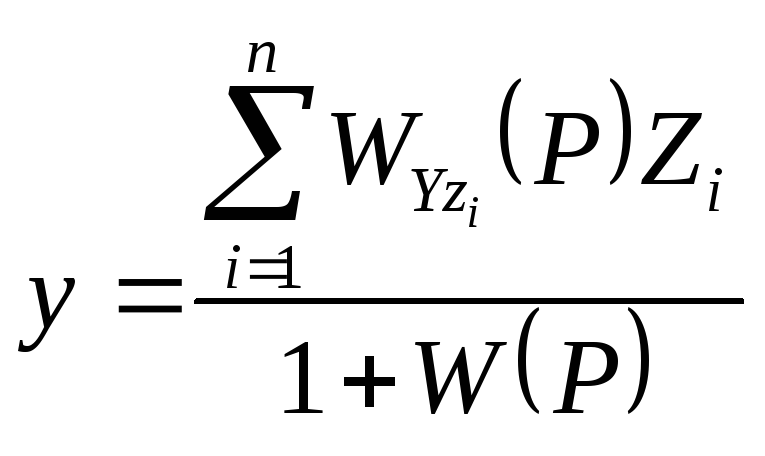. Отсюда для рассматриваемой системы получаем:(2.43). Эти уравнения используются для исследования всех САУ.

Применяя рассмотренные правила преобразования структурной схемы, можно любую многоконтурную схемы привести к одноконтурному виду и свернуть в 1 ДЗ, ПФ которого будет являться ПФ исходной многоконтурной системы.

2. Формулировка критерия Найквиста для случая замкнутой устойчивости системы.

Первая формулировка критерия Найквиста. Если в разомкнутом состоянии САУ устойчива, то для того, чтобы она была устойчива в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ её разомкнутого контура не охватывала точку с координатами (-1, j0).

В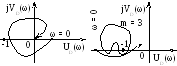торая формулировка критерия Найквиста. Неустойчивая в разомкнутом состоянии САУ в замкнутом состоянии является устойчивой, если число пересечений АФЧХ отрицательной вещественной полуоси левее точки (-1, j0) сверху вниз будет на m/2 больше, чем число пересечений снизу вверх (m – число корней характеристического уравнения разомкнутой САУ в правой полуплоскости).

Рис. 4.33. АФЧХ устойчивой САУ по I и II формулировкам Найквиста

1. Параметры распределения полюсов на комплексной плоскости.

2. Формулировка критерия Найквиста для обратной АФХ.

П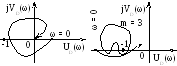ервая формулировка критерия Найквиста. Если в разомкнутом состоянии САУ устойчива, то для того, чтобы она была устойчива в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ её разомкнутого контура не охватывала точку с координатами (-1, j0).

Вторая формулировка критерия Найквиста. Неустойчивая в разомкнутом состоянии САУ в замкнутом состоянии является устойчивой, если число пересечений АФЧХ отрицательной вещественной полуоси левее точки (-1, j0) сверху вниз будет на m/2 больше, чем число пересечений снизу вверх (m – число корней характеристического уравнения разомкнутой САУ в правой полуплоскости).

Рис. 4.34. АФЧХ устойчивой САУ по I и II формулировкам Найквиста

1. Анализ устойчивости многоканальных систем с помощью логарифмического критерия Найквиста.

2. Приближённая ЛАХ звена с передаточной функцией К(Р)=1/(1+рТ).

1. Критерий Рауса.

1. Критерий Рауса-Гурвица. Применяется в случае, когда известны значение или выражение для коэффициента характерного полинома САУ: D(λ) = a_nλ_n + a_n-1λ_n-1 + … + +a₁λ₁ + +a₀ (4.5). Учёными Русом и Гурвицем были предложены независимо друг от друга неравенства, выполнение которых является необходимым и достаточным условием устойчивости систем с характеристическим полиномом любого порядка.

Гурвиц предложил определять устойчивость по специально составленному определителю элементами, которого являются коэффициентами характеристического полинома. Определитель Гурвица составляется по следующей схеме (по главной диагонали): записываются все коэффициенты характерного полинома от a_n-1 до a₀. Строки влево от главной диагонали дополняются коэффициентами с последовательно убывающими индексами, а вправо – с последовательно возрастающими. Вместо коэффициентов с индексами меньше 0 и больше n записываются 0. В результате определитель имеет вид:

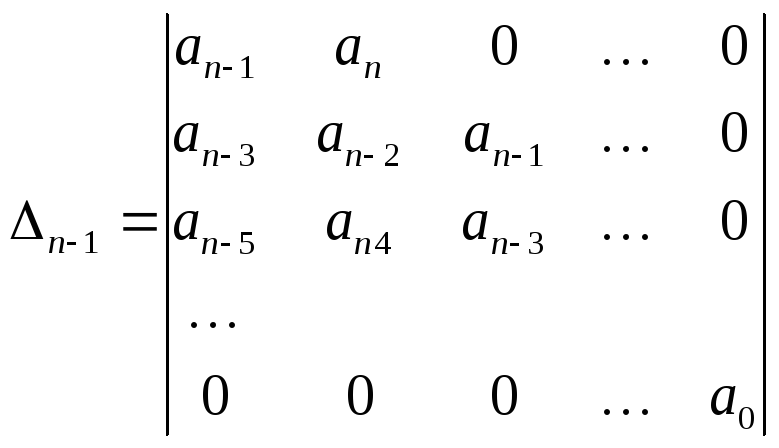. (4.6)

Критерий Гурвица: для того, чтобы САУ обладала устойчивостью необходимо и достаточно, чтобы при положительных коэффициентах характеристический полином определителя (4.6) и все его диагональные миноры были положительны.

Раус предложил определять устойчивость по значению коэффициентов в специально составленной таблице (4.1).

	an	an-2	an-4	…
	an-1	an-3	an-5	…
	C13 = an-2 – r0an-3	C23 = an-4 – r0an-5	C33 = an-6 – r0an-7	…
	C14 = an-3 – r1C23	C24 = an-5 – r1C33	C34 = an-7 – r1C43	…
	C15 = C23 – r2C24	C25 = C33 – r2C34	C35 = C43 – r2C44	…

В строках 1 и 2 – коэффициенты характерного полинома. Коэффициенты в остальных строках соединены формулами: C_k,i= C_k+1,i-2 – r_i-1C_k+1,i-1, .

Критерий Рауса формулируется следующим образом: для того, чтобы САУ была устойчива необходимо и достаточно, чтобы при положительных коэффициентах первой линии все коэффициенты первого столбца были положительны.

Часто критерии Рауса-Гурвица не разделяются, т.к. они представляют одно и тоже, но в расширенной теории автоматического управления эти критерии рассматриваются на основе теории высшей математики в разных разделах, т.к. вычисление значения определителя Гурвица наиболее эффективно производить путём приведения его к диагональной форме, при этом элементы такого определителя становятся коэффициентами таблицы Рауса.

2. Расположение нулей и полюсов на комплексной плоскости.

1. Графоаналитический метод расчёта переходного процесса.

2. Критерий Михайлова с изображением годографа.

Критерий Михайлова- это частотный критерий, позволяющий судить об устойчивости замкнутой или разомкнутой системы по поведению её характеристического вектора на комплексной плоскости.

Критерий Михайлова является графоаналитическим методом оценки устойчивости с помощью годографа Михайлова характеристического вектора.

Подставив в характеристический полином (4.5) вместо λ переменную jω, получим комплексную функцию: D(jω) = a_n(jω)ⁿ + a_n-1(jω)^n-1 + … + a₁(jω) + a₀ (4.12). После возведения в соответствующие степени, выражение (4.10) можно разбить на вещественную и мнимую части: D(jω) = U_D(ω) + jV_D(ω) (4.13), где (4.14)

Далее задав дискретные значенияω от 0 до ∞ можно вычислить соответствующие им значения U_D(ω) и V_D(ω) и по ним на комплексной плоскости построить годограф Михайлова.

Рис. 4.35. Графоаналитический критерий Михайлова (годограф Михайлова)

Представив выражение (4.13) в виде D(jω) = D(ω)e^jφ(ω) можно построить в полярных координатах годограф Михайлова, который начертит своим концом вектор, изменяясь по модулю и направлению с изменением частоты.

Первая формулировка критерия Михайлова: для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до ∞, начав своё движение с вещественной положительной полуоси, прошёл бы последовательно в положительном направлении (против часовой стрелки), нигде не обращаясь в 0, n квадрантов, где n – степень характеристического полинома. В последнем квадранте годограф должен уйти в бесконечность. При переходе годографа из одного квадранта в другой попеременно обращаются в 0 его вещественная и мнимая части. Отсюда вытекает следствие из критерия Михайлова: для устойчивости системы корни уравнений U_D(ω) = 0 и V_D(ω) = 0 должны чередоваться (условия перемежаемости корней) и общее число этих корней должно быть равно порядку характеристического полинома.

Вторая формулировка критерия Михайлова (критерий перемежаемости корней): для устойчивости системы необходимо и достаточно, чтобы корни уравнений U_D(ω) = 0 и V_D(ω) = 0 перемежались при условии ω_v1 = 0 < ω_u1 < ω_v2 < ω_u2 < ω_v3 < …. Этой формулировкой удобно пользоваться для исследования устойчивости систем, описываемых ДУ до 5-го порядка включительно.

1. Основные формулы для преобразования структурных схем САУ.