1. Общие понятия и сведения об элементах САУ.

Автоматическое управление – управление, осуществляемое с помощью специальных технических систем без непосредственного участия человека.

Автоматическая система управления – совокупность правил обмена данными и требований, предъявляемых к элементам и объектам с применением средств вычислительной техники и участием в интерактивном режиме. Автоматическое управление обеспечивает высокую точность и быстродействие технических систем, повышает надёжность технологических процессов.

ТАУ – основная часть технической кибернетики, предназначенная для разработки общих принципов автоматического управления, методов анализа исследования функций и синтеза САУ техническими объектами.

САУ – совокупность объекта управления (ОУ) и автоматического управляющего устройства. САУ функционирует под влиянием воздействий.

В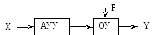оздействие – фактор, влияющий на работу САУ.

Рис. 1.1. Элементарная схема САУ

X – задающее воздействие, U – управляющее, F – возмущающее.

S = Ф{X, U, F, Y …} – формула системы.

Задающее воздействие X – внешнее воздействие, определяющее необходимый закон изменения выходной величины Y (т.н. управляемые координаты объекта управления).

Управляющее воздействие U – воздействие, поступающее от АУУ к ОУ и обеспечивающее изменение управляемой величины в соответствии с задающим воздействием X.

Зависимость U от X можно представить в виде некоторой функции / алгоритма управления, описывающей последовательность и содержание управляющего воздействия для обеспечения заданного поведения ОУ.

Возмущающее воздействие F – внешнее воздействие, нарушающее заданный закон изменения управления. Характер и состав возможных воздействий зависит от вида конкретного ОУ и условий его эксплуатации. Все возмущающие воздействия оказывают вредное влияние на работу ОУ, поэтому одной из базовых задач УУ является устранение / компенсация результатов этих воздействий.

Объекты управления (ОУ) могут быть одномерными (1 измеряемая величина). В общем случае ОУ – многомерные и могут работать под влиянием множества управляющих воздействий U и возмущающих воздействий F и иметь множество измеряемых выходных величин Y: Y = {Y₁, Y₂, … , Y_n}.

На практике при проектировании САУ по возможности стараются учитывать только основные воздействия, оказывающие наиболее существенное влияние на ОУ.

В ТАУ рассматриваются ОУ с сосредоточенными и распределёнными параметрами.

В ОУ с сосредоточенными параметрами при их математическом описании считают, что параметры объекта постоянны и сосредоточены в одной точке. Переменные, описывающие динамическое состояние объекта, – функции только времени.

В ОУ с распределёнными параметрами переменные, описывающие поведение ОУ, изменяются не только во времени, но и в пространстве, что существенно усложняет проведение их анализа и синтеза.

Все ОУ характеризуются наличием / отсутствием самовыравнивания / саморегулирования. Устойчивость – свойство ОУ самостоятельно (без участия УУ) возвращаться в исходное положение / состояние после снятия возмущения. Устойчивые объекты могут работать в одном режиме и без УУ, но недостаточно точно, поскольку отклонение управляемой величины будет пропорционально возмущающему воздействию F. Неустойчивые объекты не обладают самовыравниванием. После снятия возмущения их выходная величина без участия УУ может неограниченно изменяться до аварийного состояния / полной остановки.

Функция – полезные свойства системы.

Все автоматические системы можно разделить на системы

• автоматического контроля,

• автоматической сигнализации,

• автоматической защиты,

• автоматического управления и регулирования.

2. Частотный критерий качества переходного процесса.

При анализе качества переходного процесса частотным методом используется ЧХ замкнутой системы W(jω) = A(ω)e^jφω. Зная её, можно определить выходную величину ЧХ при подаче на вход гармонического воздействия и найти реакцию системы в переходном процессе на произведённое воздействие.

Представляя произведённое воздействие в виде бесконечной суммы гармонических колебаний, можно по ЧХ определить реакцию системы на каждое из этих элементарных колебаний, затем, просуммировав все реакции, найти результирующую.

Интеграл Фурье для единичной ступенчатой функции: (4.20), т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида, а реакция системы на единичную ступенчатую функцию – в виде оригинала:(4.21). Подставив вместоW(jω) = U(ω) + +jY(ω), получим: , гдеU(ω) – вещественная ЧХ системы.

Т.о. в частотном методе анализа косвенной характеристикой качества является вещественная ЧХ САУ.

К устойчивым критериям САУ относится показатель колебательности, резонансная частота, перерегулирование.

Частотный метод оценки качества справедлив для линейно-фазовых систем – систем, у которых при одинаковой АЧХ фазовые ЧХ имеют минимальное значение по модулю. Колебательность и длительность переходного процесса можно приблизительно оценить по вещественной ЧХ (ВЧХ) замкнутой САУ.

Если ВЧХ имеет вид кривой 1, то переходная характеристика не имеет перерегулирования. Для кривой 2 при относительном максимуме характеристики величина перерегулированияσ ≤ 18%. Кривые 3 и 4 соответствуют колебательному переходному процессу и колебательность тем больше, чем больше величина относительного максимума.

Если U_max(ω) = 1,2 (кривая 3), то σ ≤ 50% (автопилот).

При (кривая4) перерегулирование возрастает ещё больше, σ ≤ 80%.

К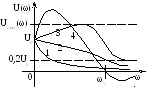роме того, если ВЧХ имеет не только положительную, но и отрицательную часть (кривая4), то колебательность возрастает. Длительность переходного процесса можно примерно определить по величине частотного диапазона, при котором ВЧХ будет положительна (кривая 4), или пока она не станет меньше 0,2U(0) (кривые 1-3). Этот частотный диапазон ω₊ называется интервалом положительности и определяет длительность переходного процесса: (4.23).

Для ВЧХ, у которых U_max(ω) ≤ U(0) (кривые 1,2) K = 4. С возрастанием величины относительного максимума K увеличивается.

Р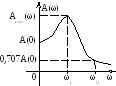ис.4.2. Приблизительные переходные характеристики, оцениваемые по ВЧХ замкнутой САУ

Рис. 4.3. Оценка качества регулирования по АЧХ САУ

Для оценки качества регулирования часто используется АЧХ САУ. По АЧХ замкнутой САУ можно определить колебательность системы по показателю колебательности M, численно равному отношению максимального значения АЧХ к его значению при ω=0: чем больше значение M, тем сильнее колебательность системы, и тем больше длительность колебательного процесса.

Качество переходного процесса считается удовлетворительным, если M[1,1;1,5]. При таком значении M переходная характеристика имеет слабую колебательность с частотой, близкой к резонансной ω_р, которая также является критерием качества. На этой частоте гармонические колебания проходят через систему с наибольшим усилением. Резонансная частота ω_р позволяет примерно определить время достижения первого максимума t_M, т.е. (4.24).

Длительность переходного процесса при предположении, что за это время в системе происходит 12 колебания, составляет (4.25).

В случае колебательной переходной характеристики резонансная частота ω_р замкнутой САУ близка к частоте среза ω_ср ЛЧХ замкнутой САУ, которая является также показателем качества.

Интервал частот, при котором выполняется условие A(ω) ≤ 0,707A(0) (4.26) называется полосой пропускания частот замкнутой САУ. Она связана с длительностью переходного процесса обратной зависимостью: чем шире полоса пропускания системы, тем меньше длительность переходного процесса. И наоборот: чем больше инерционность САУ, тем уже будет её полоса пропускания, и тем ближе она по своим свойствам к фильтру низких частот. Такая система является более точной, т.к. она хорошо пропускает информационные, как правило, низкочастотные, и задерживает высокочастотные помехи.

1. Расчёт переходного процесса при известном расположении нулей и полюсов выходной координаты САУ.

2. Воздействия и сигналы.

В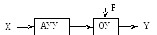оздействие – фактор, влияющий на работу САУ.

Рис. 1.4. Элементарная схема САУ

X – задающее воздействие, U – управляющее, F – возмущающее.

S = Ф{X, U, F, Y …} – формула системы.

Задающее воздействие X – внешнее воздействие, определяющее необходимый закон изменения выходной величины Y (т.н. управляемые координаты объекта управления).

Управляющее воздействие U – воздействие, поступающее от АУУ к ОУ и обеспечивающее изменение управляемой величины в соответствии с задающим воздействием X.

Зависимость U от X можно представить в виде некоторой функции / алгоритма управления, описывающей последовательность и содержание управляющего воздействия для обеспечения заданного поведения ОУ.

Возмущающее воздействие F – внешнее воздействие, нарушающее заданный закон изменения управления. Характер и состав возможных воздействий зависит от вида конкретного ОУ и условий его эксплуатации. Все возмущающие воздействия оказывают вредное влияние на работу ОУ, поэтому одной из базовых задач УУ является устранение / компенсация результатов этих воздействий.

Объекты управления (ОУ) могут быть одномерными (1 измеряемая величина). В общем случае ОУ – многомерные и могут работать под влиянием множества управляющих воздействий U и возмущающих воздействий F и иметь множество измеряемых выходных величин Y: Y = {Y₁, Y₂, … , Y_n}.

На практике при проектировании САУ по возможности стараются учитывать только основные воздействия, оказывающие наиболее существенное влияние на ОУ.

В ТАУ рассматриваются ОУ с сосредоточенными и распределёнными параметрами.

1. Принципы построения САУ и их классификация.

Частотные критерии качества

При анализе качества переходного процесса частотным методом используется ЧХ замкнутой системы W(jω) = A(ω)e^jφω. Зная её, можно определить выходную величину ЧХ при подаче на вход гармонического воздействия и найти реакцию системы в переходном процессе на произведённое воздействие.

Представляя произведённое воздействие в виде бесконечной суммы гармонических колебаний, можно по ЧХ определить реакцию системы на каждое из этих элементарных колебаний, затем, просуммировав все реакции, найти результирующую.

Интеграл Фурье для единичной ступенчатой функции: (4.20), т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида, а реакция системы на единичную ступенчатую функцию – в виде оригинала:(4.21). Подставив вместоW(jω) = U(ω) + +jY(ω), получим: , гдеU(ω) – вещественная ЧХ системы.

Т.о. в частотном методе анализа косвенной характеристикой качества является вещественная ЧХ САУ.

К устойчивым критериям САУ относится показатель колебательности, резонансная частота, перерегулирование.

Частотный метод оценки качества справедлив для линейно-фазовых систем – систем, у которых при одинаковой АЧХ фазовые ЧХ имеют минимальное значение по модулю. Колебательность и длительность переходного процесса можно приблизительно оценить по вещественной ЧХ (ВЧХ) замкнутой САУ.

Если ВЧХ имеет вид кривой 1, то переходная характеристика не имеет перерегулирования. Для кривой 2 при относительном максимуме характеристики величина перерегулированияσ ≤ 18%. Кривые 3 и 4 соответствуют колебательному переходному процессу и колебательность тем больше, чем больше величина относительного максимума.

Если U_max(ω) = 1,2 (кривая 3), то σ ≤ 50% (автопилот).

При (кривая4) перерегулирование возрастает ещё больше, σ ≤ 80%.

Кроме того, если ВЧХ имеет не только положительную, но и отрицательную часть (кривая4), то колебательность возрастает. Длительность переходного процесса можно примерно определить по величине частотного диапазона, при котором ВЧХ будет положительна (кривая 4), или пока она не станет меньше 0,2U(0) (кривые 1-3). Этот частотный диапазон ω₊ называется интервалом положительности и определяет длительность переходного процесса: (4.23).

Для ВЧХ, у которых U_max(ω) ≤ U(0) (кривые 1,2) K = 4. С возрастанием величины относительного максимума K увеличивается.

Р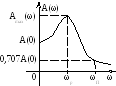ис.4.5. Приблизительные переходные характеристики, оцениваемые по ВЧХ замкнутой САУ

Рис. 4.6. Оценка качества регулирования по АЧХ САУ

Для оценки качества регулирования часто используется АЧХ САУ. По АЧХ замкнутой САУ можно определить колебательность системы по показателю колебательности M, численно равному отношению максимального значения АЧХ к его значению при ω=0: чем больше значение M, тем сильнее колебательность системы, и тем больше длительность колебательного процесса.

Качество переходного процесса считается удовлетворительным, если M[1,1;1,5]. При таком значении M переходная характеристика имеет слабую колебательность с частотой, близкой к резонансной ω_р, которая также является критерием качества. На этой частоте гармонические колебания проходят через систему с наибольшим усилением. Резонансная частота ω_р позволяет примерно определить время достижения первого максимума t_M, т.е. (4.24).

Длительность переходного процесса при предположении, что за это время в системе происходит 12 колебания, составляет (4.25).

В случае колебательной переходной характеристики резонансная частота ω_р замкнутой САУ близка к частоте среза ω_ср ЛЧХ замкнутой САУ, которая является также показателем качества.

Интервал частот, при котором выполняется условие A(ω) ≤ 0,707A(0) (4.26) называется полосой пропускания частот замкнутой САУ. Она связана с длительностью переходного процесса обратной зависимостью: чем шире полоса пропускания системы, тем меньше длительность переходного процесса. И наоборот: чем больше инерционность САУ, тем уже будет её полоса пропускания, и тем ближе она по своим свойствам к фильтру низких частот. Такая система является более точной, т.к. она хорошо пропускает информационные, как правило, низкочастотные, и задерживает высокочастотные помехи.

2. Графоаналитический метод расчёта переходного процесса.

1. Оценка показателей качества переходной характеристики по распределению корней на комплексной плоскости.

2. Элементы и звенья САУ.