Критерии устойчивости:
I. Алгебраические.
1. Критерий Рауса-Гурвица. Применяется в случае, когда известны значение или выражение для коэффициента характерного полинома САУ: D(λ) = anλn + an-1λn-1 + … + +a1λ1 + +a0 (4.5). Учёными Русом и Гурвицем были предложены независимо друг от друга неравенства, выполнение которых является необходимым и достаточным условием устойчивости систем с характеристическим полиномом любого порядка.
Гурвиц предложил определять устойчивость по специально составленному определителю элементами, которого являются коэффициентами характеристического полинома. Определитель Гурвица составляется по следующей схеме (по главной диагонали): записываются все коэффициенты характерного полинома от an-1 до a0. Строки влево от главной диагонали дополняются коэффициентами с последовательно убывающими индексами, а вправо – с последовательно возрастающими. Вместо коэффициентов с индексами меньше 0 и больше n записываются 0. В результате определитель имеет вид:
.
(4.6)
Критерий Гурвица: для того, чтобы САУ обладала устойчивостью необходимо и достаточно, чтобы при положительных коэффициентах характеристический полином определителя (4.6) и все его диагональные миноры были положительны.
Раус предложил определять устойчивость по значению коэффициентов в специально составленной таблице (4.1).
|
|
an |
an-2 |
an-4 |
… |
|
|
an-1 |
an-3 |
an-5 |
… |
|
|
C13 = an-2 – r0an-3 |
C23 = an-4 – r0an-5 |
C33 = an-6 – r0an-7 |
… |
|
|
C14 = an-3 – r1C23 |
C24 = an-5 – r1C33 |
C34 = an-7 – r1C43 |
… |
|
|
C15 = C23 – r2C24 |
C25 = C33 – r2C34 |
C35 = C43 – r2C44 |
… |
В строках 1 и 2 –
коэффициенты характерного полинома.
Коэффициенты в остальных строках
соединены формулами: Ck,i=
Ck+1,i-2
– ri-1Ck+1,i-1,
.
Критерий Рауса формулируется следующим образом: для того, чтобы САУ была устойчива необходимо и достаточно, чтобы при положительных коэффициентах первой линии все коэффициенты первого столбца были положительны.
Часто критерии Рауса-Гурвица не разделяются, т.к. они представляют одно и тоже, но в расширенной теории автоматического управления эти критерии рассматриваются на основе теории высшей математики в разных разделах, т.к. вычисление значения определителя Гурвица наиболее эффективно производить путём приведения его к диагональной форме, при этом элементы такого определителя становятся коэффициентами таблицы Рауса.
2. Критерий Льенора-Шипара. Является модификацией критерия Гурвица. Если при выходных положительных коэффициентах характерного полинома всем миноры с чётными индексами положительны, то будет положительны и все миноры с нечётными индексами. Критерий формулируется следующим образом: для того, чтобы САУ была устойчивой, необходимо, чтобы при всех положительных коэффициентах характеристического полинома с чётными или нечётными индексами.
По сравнению с критерием Гурвица критерий Льенора-Шипара требует меньше вычислений, что при использовании ЭВМ не является существенным препятствием.
3. Модернизированный алгебраический критерий устойчивости. Основным достоинством алгебраических критериев устойчивости является удобство их использования на ЭВМ, кроме того, задача решается в общих параметрах, т.к. коэффициенты характерного уравнения достаточно просто выражаются через физические характеристики исследуемой системы.
На практике большой интерес представляет диапазон изменения параметров САУ, в пределах которого может быть обеспечена устойчивость. Так диапазон запаса устойчивости определяет допуск на разброс физических характеристик системы.
Классические алгебраические критерии устанавливают только сам факт устойчивости и не позволяют получить информацию о запасах устойчивости САУ и определить, как изменить параметры системы, чтобы сделать её устойчивой.
На практике исследование САУ со сложной структурой с использованием алгебраических критериев затруднительно из-за возникающей ошибки расчётов и необходимости судить об устойчивости по знаку разности слишком больших и слишком малых чисел. Эти недостатки ограничивают использование алгебраических критериев в инженерной практике при проектировании САУ.
Рассмотрим расчёт устойчивости на примере критерия Гурвица. Преобразуем традиционную форму критерия Гурвица, воспользуемся одним из основных определителей и вынесем из определителя (4.6) произведение его главной диагонали.
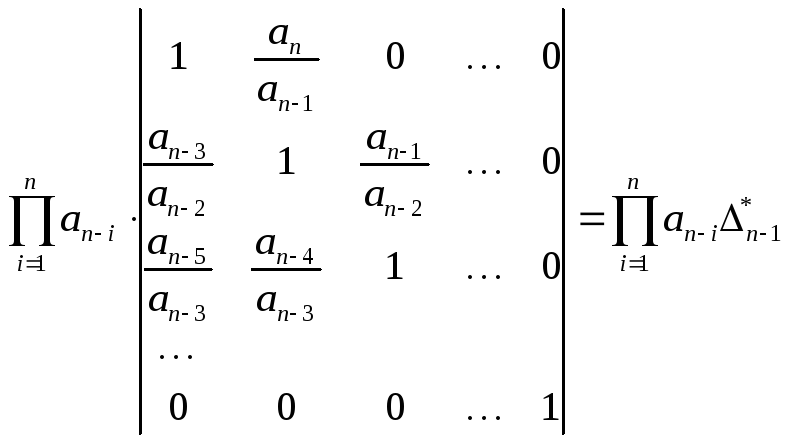(4.7).
Определитель Δn-1* называется страшим безразмерным определителем Гурвица.
Из выражения (4.7) следует, что критерий Гурвица не теряет справедливости и при оценке устойчивости по безразмерному определителю и его диагональным минорам, так как коэффициенты характеристического полинома должны быть положительны.
Представив выражение (4.7) в диагональной форме, можно получить выражение для коэффициентов таблицы Рауса.
Наиболее ценными оказываются следующие свойства безразмерной формы алгебраических критериев для устойчивой системы:
1. Значение определителя Гурвица (и его диагональных миноров) м коэффициентов таблицы Рауса в безразмерной форме лежат в пределах от 0 до ∞.
2. Значение определителя Гурвица и миноров безразмерной формы определителя Гурвица с увеличением их порядка уменьшается. Наименьшее значение имеет старший безразмерный определитель Гурвица.
3. Безразмерные коэффициенты таблицы Рауса располагаются в строках таблицы в порядке увеличения их значения слева направо, что является новым дополнительным необходимым условием устойчивости и адекватно условию перемежения корней действительной и мнимой частей частотных характеристик.
При поведении
расчётов с помощью безразмерной формы
критериев используют следующую
характеристику устойчивости САУ, на
практике называемую коэффициентом
устойчивости:
(4.8), гдеk
= 1, 2, …, n
(n
– порядок полинома).
При помощи коэффициента устойчивости формулируется дополнительное необходимое условие устойчивости, более жёсткое, чем положительность коэффициентов характеристического полинома, т.е. 0 ≤ Mk ≤ 1 (4.9), которое способствует существенному упрощению анализа устойчивости. Чем ближе Mk к 0, тем большими запасами устойчивости обладает система.
Следует отметить, что условие 0 ≤ Mk ≤ 0,4655 (k = 1,2,…n-2) является достаточным условием устойчивости САУ с характеристически полиномом любого порядка.
При использовании коэффициентов устойчивости, например, по критериям Гурвица, необходимые и достаточные условия устойчивости САУ с характеристическим полиномом 3-5 порядка имеют следующий практический вид:
n = 3: 1 – M1 ≥ 0;
n = 4: 1 – M1 – M2 ≥ 0;
n = 5: (1 – M1)(1 – M3) – M2(1 – M1M2)2 ≥ 0.
Коэффициент устойчивости служит исходными данными и для критерия Рауса. Таблица коэффициентов Рауса в безразмерной форме записывается начиная со строки 3, т.к. в строках 1-2 вместо коэффициентов характеристического полинома стоят 1:
|
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
c11 = 1 – Mn–2 |
c23 = 1 – Mn–2Mn–4 |
c33 = 1 – Mn–2Mn–4Mn–6 |
… |
|
|
|
|
… |
|
|
|
… |
… |
Анализ устойчивости с помощью безразмерной формы алгебраических критериев целесообразно проводить по следующему алгоритму:
1. Определяем коэффициенты характеристического полинома и вычисляем их значения;
2. Проверяем положительность коэффициентов характеристического полинома (классическое необходимое условие устойчивости);
3. Вычисляем значение коэффициента устойчивости (4.8) и проверяем выполнение условия устойчивости (4.9).
4. Вычисляем значение безразмерных определителей Гурвица или коэффициентов таблицы Рауса (при использовании критерия Рауса учитывается дополнительное необходимое условие устойчивости) и проверяем выполнение необходимого и достаточного условия устойчивости.
В случае невыполнения на каком-либо этапе анализа устойчивости требований условий устанавливается факт неустойчивости системы. При этом характеристики безразмерной формы алгебраических критериев позволят определить коэффициенты характеристического полинома, от которого зависит неустойчивость, и выработать рекомендации для изменения исследуемой системы с целью обеспечения её устойчивости.
При расчёте на ЭВМ безразмерная форма алгебраических критериев может применяться для анализа устойчивости системы с характеристически полиномом любого порядка. С точки зрения практических расчётов она обладает ценным свойством: значения безразмерных алгебраических характеристик не зависит от масштаба коэффициентов характеристического полинома. Кроме того, значение безразмерного определителя Гурвица и коэффициентов Рауса представляет собой числовые характеристики запасов устойчивости. Например, для устойчивой системы с характеристическим полиномом 4-го порядка значение старшего порядка определителя Гурвица равно максимальному допуску на величину коэффициента характеристического полинома, в пределах которого система сохраняет устойчивость.
В общем случае значение старшего безразмерного определителя Гурвица для абсолютно устойчивой системы близко к 1, а при приближении к границе устойчивости стремиться к 0.
Преимущество безразмерной формы алгебраических критериев можно проиллюстрировать на примере анализа устойчивости с помощью критерия Гурвица для 4-х САУ с характеристическими полиномами вида:
D1(s) = s9 + 9s8 +36s7 + 84s6 + 126s5 + 126s4 + 84s3 + 36s2 + 9s + 1 = (s + 1)9;
D2(s) = s9 + 1,8s8 +1,44s7 + 0,672s6 + 0,201s5 + 0,04032s4 + 5,376·10-3s3 + 4,608·10-4s2 + +2,3·10-5s + 5,12·10-6 = (s + 0,2)9;
D3(s) = s9 + 2,6s8 +6,56s7 + 10,016s6 + 13,001s5 + 13,0016s4 + 10,016s3 + 6,56s2 + 2,6s + 1= = (s2 + 0,4s + 1)4(s + 1);
D4(s)
= s9
+ 555s8
+28060s7
+ 140400s6
+ 70220s5
+ 35125s4
+ 17,55s3
+ 0,00877s2
+ +4,34·10-7s
+ 1,953·10-12
=
.
Значения определителя Гурвица Таблица 4.2.
|
№ п/п |
Δ1 |
Δ2 |
Δ3 |
Δ4 |
Δ5 |
Δ6 |
Δ7 |
Δ8 |
|
|
9 |
240 |
0,0011 |
6,1·105 |
2,9·107 |
9,0·108 |
1,3·1010 |
6,9·1010 |
|
|
1,8 |
1,92 |
0,71 |
0,062 |
9,5·10-4 |
1,9·10-6 |
3,6·10-10 |
4,7·10-15 |
|
|
2,6 |
7,04 |
16,4 |
20,7 |
30,4 |
6,98 |
7,22 |
0,058 |
|
|
555 |
1,5·107 |
2,0·1012 |
1,5·1017 |
5,2·1020 |
9,0·1021 |
7,8·1019 |
3,4·1012 |
Значения безразмерного определителя Гурвица Таблица 4.3.
|
№ п/п |
Δ1* |
Δ2* |
Δ3* |
Δ4* |
Δ5* |
Δ6* |
Δ7* |
Δ8* |
|
|
1 |
0,741 |
0,407 |
0,177 |
0,0671 |
0,0248 |
0,0130 |
0,00584 |
|
|
1 |
0,741 |
0,407 |
0,177 |
0,0671 |
0,0248 |
0,0130 |
0,00584 |
|
|
1 |
0,413 |
0,096 |
0,0093 |
0,0011 |
2,2·10-5 |
3,8·10-6 |
1,2·10-8 |
|
|
1 |
0,991 |
0,981 |
0,971 |
0,961 |
0,952 |
0,942 |
0,933 |
Анализ числовых значений определителя Гурвица показывает только, что рассмотренная система устойчива. При этом разброс численных значений очень широк.
По значению безразмерного определителя Гурвица кроме установления факта устойчивости системы сравнивая значения старших определителей можно утверждать, что системы с характеристическими полиномами 1 и 2 идентичны с толчки зрения запаса устойчивости. Система с характеристическим полиномом 2 обладает малым, а система с характеристическим полиномом 4 – большим запасами устойчивости. Это соответствует действительности.
Т.о. безразмерная форма алгебраических критериев устойчивости позволяет решать многие проблемы.
Критерий Гурвица.
1. Критерий Рауса-Гурвица. Применяется в случае, когда известны значение или выражение для коэффициента характерного полинома САУ: D(λ) = anλn + an-1λn-1 + … + +a1λ1 + +a0 (4.5). Учёными Русом и Гурвицем были предложены независимо друг от друга неравенства, выполнение которых является необходимым и достаточным условием устойчивости систем с характеристическим полиномом любого порядка.
Гурвиц предложил определять устойчивость по специально составленному определителю элементами, которого являются коэффициентами характеристического полинома. Определитель Гурвица составляется по следующей схеме (по главной диагонали): записываются все коэффициенты характерного полинома от an-1 до a0. Строки влево от главной диагонали дополняются коэффициентами с последовательно убывающими индексами, а вправо – с последовательно возрастающими. Вместо коэффициентов с индексами меньше 0 и больше n записываются 0. В результате определитель имеет вид:
.
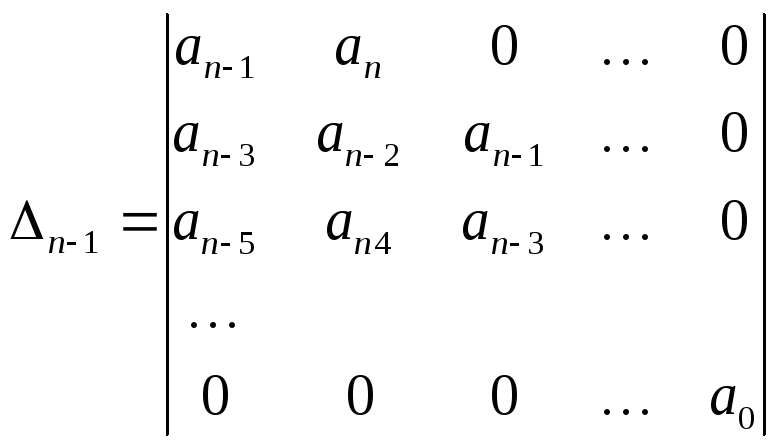(4.6)
Критерий Гурвица: для того, чтобы САУ обладала устойчивостью необходимо и достаточно, чтобы при положительных коэффициентах характеристический полином определителя (4.6) и все его диагональные миноры были положительны.
Раус предложил определять устойчивость по значению коэффициентов в специально составленной таблице (4.1).
|
|
an |
an-2 |
an-4 |
… |
|
|
an-1 |
an-3 |
an-5 |
… |
|
|
C13 = an-2 – r0an-3 |
C23 = an-4 – r0an-5 |
C33 = an-6 – r0an-7 |
… |
|
|
C14 = an-3 – r1C23 |
C24 = an-5 – r1C33 |
C34 = an-7 – r1C43 |
… |
|
|
C15 = C23 – r2C24 |
C25 = C33 – r2C34 |
C35 = C43 – r2C44 |
… |
В строках 1 и 2 –
коэффициенты характерного полинома.
Коэффициенты в остальных строках
соединены формулами: Ck,i=
Ck+1,i-2
– ri-1Ck+1,i-1,
.
Критерий Рауса формулируется следующим образом: для того, чтобы САУ была устойчива необходимо и достаточно, чтобы при положительных коэффициентах первой линии все коэффициенты первого столбца были положительны.
Часто критерии Рауса-Гурвица не разделяются, т.к. они представляют одно и тоже, но в расширенной теории автоматического управления эти критерии рассматриваются на основе теории высшей математики в разных разделах, т.к. вычисление значения определителя Гурвица наиболее эффективно производить путём приведения его к диагональной форме, при этом элементы такого определителя становятся коэффициентами таблицы Рауса.
Системы первого и второго рода. Запасы устойчивости.
Переходные процессы САУ. Методика учёта начальных условий.
Критерий Рауса.
1. Критерий Рауса-Гурвица. Применяется в случае, когда известны значение или выражение для коэффициента характерного полинома САУ: D(λ) = anλn + an-1λn-1 + … + +a1λ1 + +a0 (4.5). Учёными Русом и Гурвицем были предложены независимо друг от друга неравенства, выполнение которых является необходимым и достаточным условием устойчивости систем с характеристическим полиномом любого порядка.
Гурвиц предложил определять устойчивость по специально составленному определителю элементами, которого являются коэффициентами характеристического полинома. Определитель Гурвица составляется по следующей схеме (по главной диагонали): записываются все коэффициенты характерного полинома от an-1 до a0. Строки влево от главной диагонали дополняются коэффициентами с последовательно убывающими индексами, а вправо – с последовательно возрастающими. Вместо коэффициентов с индексами меньше 0 и больше n записываются 0. В результате определитель имеет вид:
.
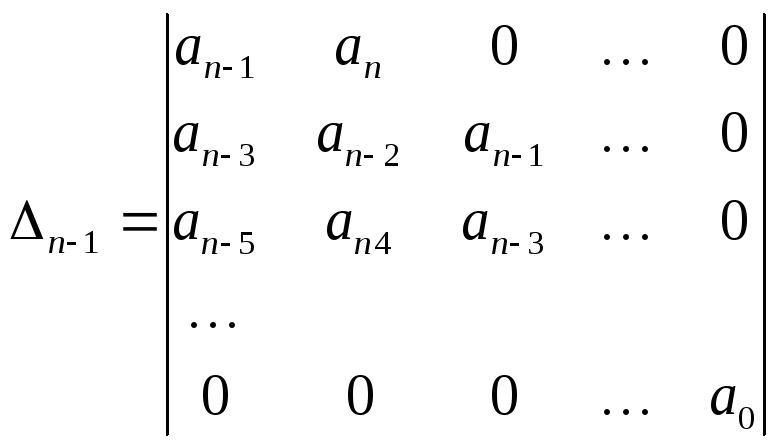(4.6)
Критерий Гурвица: для того, чтобы САУ обладала устойчивостью необходимо и достаточно, чтобы при положительных коэффициентах характеристический полином определителя (4.6) и все его диагональные миноры были положительны.
Раус предложил определять устойчивость по значению коэффициентов в специально составленной таблице (4.1).
|
|
an |
an-2 |
an-4 |
… |
|
|
an-1 |
an-3 |
an-5 |
… |
|
|
C13 = an-2 – r0an-3 |
C23 = an-4 – r0an-5 |
C33 = an-6 – r0an-7 |
… |
|
|
C14 = an-3 – r1C23 |
C24 = an-5 – r1C33 |
C34 = an-7 – r1C43 |
… |
|
|
C15 = C23 – r2C24 |
C25 = C33 – r2C34 |
C35 = C43 – r2C44 |
… |
В строках 1 и 2 –
коэффициенты характерного полинома.
Коэффициенты в остальных строках
соединены формулами: Ck,i=
Ck+1,i-2
– ri-1Ck+1,i-1,
.
Критерий Рауса формулируется следующим образом: для того, чтобы САУ была устойчива необходимо и достаточно, чтобы при положительных коэффициентах первой линии все коэффициенты первого столбца были положительны.
Часто критерии Рауса-Гурвица не разделяются, т.к. они представляют одно и тоже, но в расширенной теории автоматического управления эти критерии рассматриваются на основе теории высшей математики в разных разделах, т.к. вычисление значения определителя Гурвица наиболее эффективно производить путём приведения его к диагональной форме, при этом элементы такого определителя становятся коэффициентами таблицы Рауса.
Критерий Михайлова.
Критерий Михайлова- Это частотный критерий, позволяющий судить об устойчивости замкнутой или разомкнутой системы по поведению её характеристического вектора на комплексной плоскости.
Критерий Михайлова является графоаналитическим методом оценки устойчивости с помощью годографа Михайлова характеристического вектора.
Подставив в
характеристический полином (4.5) вместо
λ
переменную jω,
получим комплексную функцию: D(jω)
= an(jω)n
+ an-1(jω)n-1
+ … + a1(jω)
+ a0
(4.12). После возведения в соответствующие
степени, выражение (4.10) можно разбить
на вещественную и мнимую части: D(jω)
= UD(ω)
+ jVD(ω)
(4.13), где
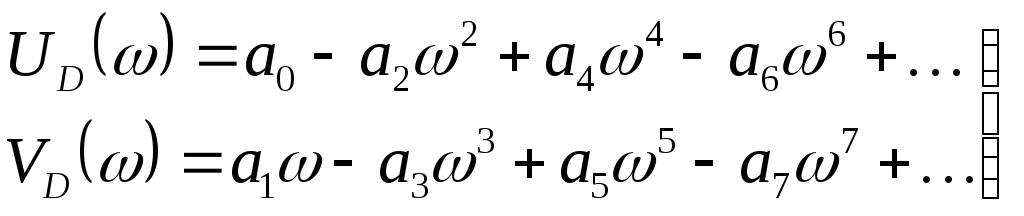(4.14)
Д
алее
задав дискретные значенияω
от 0
до ∞ можно вычислить соответствующие
им значения UD(ω)
и VD(ω)
и по ним на комплексной плоскости
построить годограф Михайлова.
Рис. 4.21. Графоаналитический критерий Михайлова (годограф Михайлова)
Представив выражение (4.13) в виде D(jω) = D(ω)ejφ(ω) можно построить в полярных координатах годограф Михайлова, который начертит своим концом вектор, изменяясь по модулю и направлению с изменением частоты.
Первая формулировка критерия Михайлова: для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до ∞, начав своё движение с вещественной положительной полуоси, прошёл бы последовательно в положительном направлении (против часовой стрелки), нигде не обращаясь в 0, n квадрантов, где n – степень характеристического полинома. В последнем квадранте годограф должен уйти в бесконечность. При переходе годографа из одного квадранта в другой попеременно обращаются в 0 его вещественная и мнимая части. Отсюда вытекает следствие из критерия Михайлова: для устойчивости системы корни уравнений UD(ω) = 0 и VD(ω) = 0 должны чередоваться (условия перемежаемости корней) и общее число этих корней должно быть равно порядку характеристического полинома.
Вторая формулировка критерия Михайлова (критерий перемежаемости корней): для устойчивости системы необходимо и достаточно, чтобы корни уравнений UD(ω) = 0 и VD(ω) = 0 перемежались при условии ωv1 = 0 < ωu1 < ωv2 < ωu2 < ωv3 < …. Этой формулировкой удобно пользоваться для исследования устойчивости систем, описываемых ДУ до 5-го порядка включительно.
Частотный метод оценки качества в переходных процессах САУ.