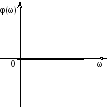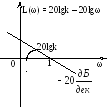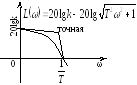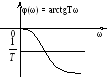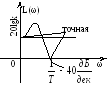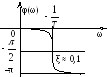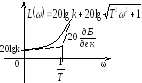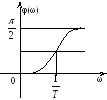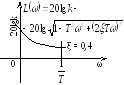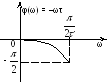Типовые динамические звенья
Передаточные функции сложных динамических элементов можно представить в виде выражения, состоящего из произведения простых сомножителей первого / второго порядка.
При анализе динамических свойств САУ часто оказывается удобно вводить в рассмотрение понятие элементарных звеньев как некоторых простых элементов САУ.
Типовые звенья – стандартные составные части элементов САУ, описываемые ДУ не выше второго порядка. Все элементарные звенья по характеру процессов, происходящих в них, можно разбить на следующие типы.
1. Усилительное звено. Тип звена однозначно определяется законам, связывающим между собой величины на входе x и выходе y. Для усилительного звена, которое из-за отсутствия переходных процессов иногда называют безинерционным / статическим, описываемого законом y = kx (2.23), переходная функция записывается: h(t) = k. Этот закон является наиболее простым и состоит в следующем преобразовании: входной сигнал умножается на постоянную величину k, называемую коэффициентом усиления. Он может иметь любое действительное значение (положительное / отрицательное).
Передаточная функция: W(P) = k (2.24).
Р ис.2.7. Выходная величина
при скачкообразном изменении входной
величины.
ис.2.7. Выходная величина
при скачкообразном изменении входной
величины.
2. Интегрирующее
звено.
Характеризуется тем, что скорость
изменения выходной величины пропорциональна
входной величине:
![]() (2.25).Переходная
функция:
h(t)=kt.
Интегрирующее звено не может находиться
в состоянии равновесия при любом
постоянном значении входного сигнала.
Передаточная
функция:
(2.25).Переходная
функция:
h(t)=kt.
Интегрирующее звено не может находиться
в состоянии равновесия при любом
постоянном значении входного сигнала.
Передаточная
функция:
![]() (2.26).
(2.26).
Р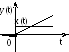 ис.2.8. Переходная функция
интегрирующего звена
ис.2.8. Переходная функция
интегрирующего звена
3 .Апериодическое
звено.
Уравнение:
.Апериодическое
звено.
Уравнение:
![]() (2.27),T
= [с] –
постоянная времени апериодического
звена, k
– коэффициент усиления / статический
коэффициент передачи. Переходная
функция:
(2.27),T
= [с] –
постоянная времени апериодического
звена, k
– коэффициент усиления / статический
коэффициент передачи. Переходная
функция:
![]() ,
приT
≥ 0 t
→ ∞,
асимптотически стремиться к установившемуся
значению k.
Передаточная
функция:
,
приT
≥ 0 t
→ ∞,
асимптотически стремиться к установившемуся
значению k.
Передаточная
функция:
![]() (2.28).
(2.28).
Рис. 2.9. Переходная функция апериодического звена
4. Колебательное
звено.
Уравнение второго порядка:
![]() (2.29).Переходная
функция:
(2.29).Переходная
функция:
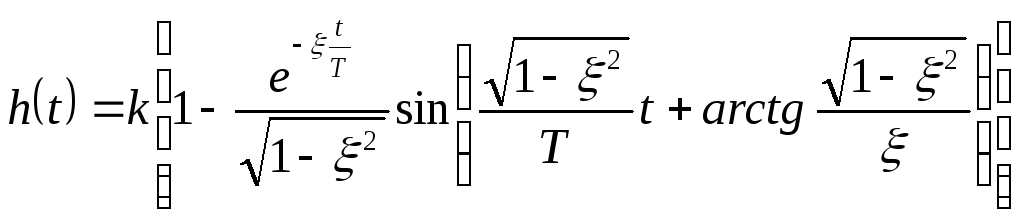 .
Описывает затухающий колебательный
процесс с относительны коэффициентом
затуханияξ
и постоянной времени T.
Форма переходного процесса зависит от
величины ξ
коэффициента затухания. При ξ
≥ 1 колебательное
звено распадается на 2 апериодических
звена (рис.2.11). Передаточная
функция:
.
Описывает затухающий колебательный
процесс с относительны коэффициентом
затуханияξ
и постоянной времени T.
Форма переходного процесса зависит от
величины ξ
коэффициента затухания. При ξ
≥ 1 колебательное
звено распадается на 2 апериодических
звена (рис.2.11). Передаточная
функция:
![]() (2.30).
(2.30).
Р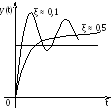 ис.2.10. Переходная функция
колебательного звена
ис.2.10. Переходная функция
колебательного звена
5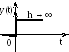 .Дифференциальное
звено первого порядка
(форсирующее звено). Уравнение:
.Дифференциальное
звено первого порядка
(форсирующее звено). Уравнение:
![]() (2.31). При скачкообразном изменении
входной величины на выходе получаем
линейный импульс с бесконечно большой
амплитудой, соответствующей бесконечно
большой скорости изменения входной
величины в момент скачка. Затем выходная
величина принимает постоянное
установившееся значение.Переходная
функция: h(t)
= =k[Tδ(t)
+ 1(t)],
δ(t)
– δ-функция, 1(t)
– единичная функция. Передаточная
функция: W(p)
= k(Ts
+ 1) (2.32).
(2.31). При скачкообразном изменении
входной величины на выходе получаем
линейный импульс с бесконечно большой
амплитудой, соответствующей бесконечно
большой скорости изменения входной
величины в момент скачка. Затем выходная
величина принимает постоянное
установившееся значение.Переходная
функция: h(t)
= =k[Tδ(t)
+ 1(t)],
δ(t)
– δ-функция, 1(t)
– единичная функция. Передаточная
функция: W(p)
= k(Ts
+ 1) (2.32).
Рис. 2.11. Переходная функция дифференцирующего звена
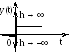 6.Дифференцирующее
звено второго порядка
(форсирующее звено второго порядка).
Уравнение:
6.Дифференцирующее
звено второго порядка
(форсирующее звено второго порядка).
Уравнение:
![]() (2.33). При скачкообразном изменении
входной величины на выходе получатся
мгновенный импульс разных знаков
бесконечно большой амплитуды,
соответствующей бесконечно большой
скорости изменения входной величины и
её производной в момент скачка. Затем
выходная величина принимает постоянное
значение.Переходная
функция:
(2.33). При скачкообразном изменении
входной величины на выходе получатся
мгновенный импульс разных знаков
бесконечно большой амплитуды,
соответствующей бесконечно большой
скорости изменения входной величины и
её производной в момент скачка. Затем
выходная величина принимает постоянное
значение.Переходная
функция:
![]() .Передаточная
функция: W(P)
= k(T2p2
+ 2ξTs
+ 1) (2.34).
.Передаточная
функция: W(P)
= k(T2p2
+ 2ξTs
+ 1) (2.34).
Рис. 2.12. Переходная функция дифференцирующего звена второго порядка
7. Звено чистого запаздывания. Выходной сигнал полностью повторяет входной сигнал, но с отставанием на некоторую величину запаздывания τ. Уравнение: y(t) = x(t – –τ) (2.35). Переходная функция: h(t) = 1(t – τ). Передаточная функция: W(P) = e-pτ (2.36).
Рис.
2.13. Переходная функция
звена чистого запаздывания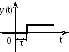
Выражения для логарифмических, амплитудных и фазных ЧХ.
Таблица 2.1. Выражения для ЛАЧХ и ЛФЧХ и их примерный вид
|
Звено |
ЛАЧХ |
ЛФЧХ |
|
Усилительное |
|
|
|
Интегрирующее |
|
|
|
Апериодическое |
|
|
|
Колебательное |
|
|
|
Дифференцирующее звено первого порядка |
|
|
|
Дифференцирующее звено второго порядка |
|
|
|
Звено чистого запаздывания |
|
|
Звенья, у которых
нет однозначной связи между частотными
характеристика, являются неустойчивыми
и имеют следующие передаточные функции
(ПФ):
![]() ;
;![]() ,
,![]() ;
;![]() .
.
У звена с передаточной
функцией
![]() АЧХ совпадает с АЧХ апериодического
звена. ФЧХ имеет вид:φ(ω)
= arctgTω
– π, при
изменении ω
от 0 до ∞ ФЧХ изменяется от –π
до –π/2.
В то время, как у апериодического
линейно-фазового звена – от 0
до –π/2.
АЧХ совпадает с АЧХ апериодического
звена. ФЧХ имеет вид:φ(ω)
= arctgTω
– π, при
изменении ω
от 0 до ∞ ФЧХ изменяется от –π
до –π/2.
В то время, как у апериодического
линейно-фазового звена – от 0
до –π/2.
Статические характеристики линейных систем с постоянными параметрами.
Влияние параметров САУ на распределение корней. Аналитический метод построения траектории корней (метод Эванса).
Определение параметров САУ по заданному распределению корней.
динамические процессы в линейных САУ описываются ДУ, связывающими выходной сигнал y(t) с входным x(t), т.е.
![]() .
(4.1)
.
(4.1)
Решение этого уравнения можно представить в виде y(t) = yсв(t) + yвын(t), где yсв – свободная составляющая выходного сигнала, зависящая от параметров САУ, yвын – вынужденная составляющая выходного сигнала, зависящая от входного воздействия.
Входной сигнал
можно рассматривать как бесконечно
малое возмущение (в виде толчка) в момент
времени t0,
являющееся постоянной величиной при t
> t0,
которое выводит систему из положения
равновесия. В этом случае вынужденную
составляющую можно не учитывать (характер
выходного сигнала будет определяться
только свободной составляющей). Общая
система уравнений (4.1) при условии
равенства 0 его правой части будет иметь
вид:
![]() (4.2), гдеAi
– постоянная интегрирования, определяемая
начальными условиями, λi
– корни следующего уравнения: anλn
+ an-1λn-1
+ … + a1λ1
+ +a0
= 0 (4.3).
(4.2), гдеAi
– постоянная интегрирования, определяемая
начальными условиями, λi
– корни следующего уравнения: anλn
+ an-1λn-1
+ … + a1λ1
+ +a0
= 0 (4.3).
Уравнение (4.3) – характерное уравнение САУ и может быть получено приравниванием к 0 характерного полинома передаточной функции.
Т.о. исследование устойчивости линейной САУ основано на использовании характерного уравнения (4.3). Необходимо отметить, что в характерном уравнении (4.3) λ уже не оператор дифференцирования, а некоторое комплексное число, определяющее в результате решения этого уравнения его корни: λi,i+1 = αi ± jωi (4.4).
Очевидно, что все слагаемые уравнения (4.2) при t → ∞ будет стремиться к 0 при условии, что αi < 0, т.е. для устойчивости линейной системы необходимо и достаточно, чтобы все корни характерного имели отрицательные действительные части. Это условие на практике называется условием устойчивости А.М.Ляпунова.
И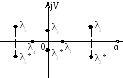 з
условия устойчивости нетрудно вывести
необходимое условие устойчивости. Для
устойчивой системы необходимо, чтобы
все коэффициенты уравнения (4.3) были бы
положительными. Далее следует отметить,
что корни характерного уравнения могут
быть действительными, мнимыми и
комплексными, т.к. характерное уравнение
имеет вещественные коэффициенты для
каждого мнимого и комплексного корня
всегда существует сопряжённый корень.
Для устойчивой системы необходимо,
чтобы все корни характерного уравнения
лежали в левой полуплоскости.
з
условия устойчивости нетрудно вывести
необходимое условие устойчивости. Для
устойчивой системы необходимо, чтобы
все коэффициенты уравнения (4.3) были бы
положительными. Далее следует отметить,
что корни характерного уравнения могут
быть действительными, мнимыми и
комплексными, т.к. характерное уравнение
имеет вещественные коэффициенты для
каждого мнимого и комплексного корня
всегда существует сопряжённый корень.
Для устойчивой системы необходимо,
чтобы все корни характерного уравнения
лежали в левой полуплоскости.
Рис. 4.14. Расположение корней характеристического уравнения на мнимой оси САУ
Вычисление корней при помощи аналитических выражений можно производить для уравнений до 4-ой степени. для уравнений более высокой степени общих выражений не существует, но для определения устойчивости нет необходимости определять значение корней. Достаточно получить информацию о знаках их вещественных частей. На этом подходе основан метод оценки без вычисления корней характерного уравнения. С помощью таких критериев можно определить влияние на устойчивость системы её параметров.
Линеаризация нелинейных статических характеристик и нелинейных уравнений.
Линеаризация – замена в уравнениях нелинейных математических операций линейными в некотором диапазоне изменения аргумента.
Л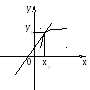 инеаризация
пометоду
касательной
заключается в разложении нелинейной
функции y
= φ(x)
в ряд Тейлора
в окрестностях точки (X0,
Y0).
Отбросив члены ряда выше первого порядка
малости, получим:
инеаризация
пометоду
касательной
заключается в разложении нелинейной
функции y
= φ(x)
в ряд Тейлора
в окрестностях точки (X0,
Y0).
Отбросив члены ряда выше первого порядка
малости, получим:
![]() ,
(2.4)
,
(2.4)![]() – значение производной функцииφ(X)X
при подстановке X
= X0.
– значение производной функцииφ(X)X
при подстановке X
= X0.
Рис. 2.15. Графический пример линеаризации
Если функция y(x)
разожжена в ряд Тейлора,
то
![]() ,y0
– начальное значение выходной величины,
соответствующее начальному значению
входной величины x0.
В окончательном виде уравнение (2.4)
запишется в виде: ΔY
≈ kΔX,
где ΔX
= X0,
ΔY
= Y
– Y0,
,y0
– начальное значение выходной величины,
соответствующее начальному значению
входной величины x0.
В окончательном виде уравнение (2.4)
запишется в виде: ΔY
≈ kΔX,
где ΔX
= X0,
ΔY
= Y
– Y0,
![]() .Геометрический
смысл такой
линеаризации (сплошная линия (рис.2.2.б),
прямая (рис.2.3)) заключается в замене
Y(X)
касательной, проведённой в точке (X0,
Y0).
Коэффициент k
в (2.5) равен тангенсу угла наклона этой
касательной к входной величине. Он
является коэффициентом пропорциональности
между отклонением входной и выходной
величин в статическом режиме и называется
коэффициентом
передачи.
.Геометрический
смысл такой
линеаризации (сплошная линия (рис.2.2.б),
прямая (рис.2.3)) заключается в замене
Y(X)
касательной, проведённой в точке (X0,
Y0).
Коэффициент k
в (2.5) равен тангенсу угла наклона этой
касательной к входной величине. Он
является коэффициентом пропорциональности
между отклонением входной и выходной
величин в статическом режиме и называется
коэффициентом
передачи.
Линеаризация по методу секущей происходит непосредственно на графике Y(X) (рис.2.2.б – пунктирная линия) таким образом, чтобы в некотором заданном диапазоне изменения входной величины X линеаризованная характеристика была как можно ближе к исходной характеристике.
Передаточный
коэффициент линеаризованной характеристики
определяется в виде:
![]() .
Таким же способом можно определитьk
при использовании метода касательной.
Этот метод даёт большую точность вблизи
рабочей точки, которая уменьшается при
переходе к границе рабочей области.
Характеристика линеаризации по методу
секущей имеет меньшее среднее расхождение
с исходной функцией.
.
Таким же способом можно определитьk
при использовании метода касательной.
Этот метод даёт большую точность вблизи
рабочей точки, которая уменьшается при
переходе к границе рабочей области.
Характеристика линеаризации по методу
секущей имеет меньшее среднее расхождение
с исходной функцией.
Методика составления дифференциальных уравнений САУ.
Приближённая оценка переходных процессов.
Интегральные оценки качества переходных процессов.
Переходная, импульсная, частотная и передаточная функции.
Переход от Y(P) к оригиналуy(t) с помощью таблицы операционных соответствий.
Вычисление интегральных квадратичных оценок (ИКО).
Точность при постоянных воздействиях.
АФХ и ЛЧХ усиленного звена.
Передаточные функции сложных динамических элементов можно представить в виде выражения, состоящего из произведения простых сомножителей первого / второго порядка.
При анализе динамических свойств САУ часто оказывается удобно вводить в рассмотрение понятие элементарных звеньев как некоторых простых элементов САУ.
Типовые звенья – стандартные составные части элементов САУ, описываемые ДУ не выше второго порядка. Все элементарные звенья по характеру процессов, происходящих в них, можно разбить на следующие типы.
1. Усилительное звено. Тип звена однозначно определяется законам, связывающим между собой величины на входе x и выходе y. Для усилительного звена, которое из-за отсутствия переходных процессов иногда называют безинерционным / статическим, описываемого законом y = kx (2.23), переходная функция записывается: h(t) = k. Этот закон является наиболее простым и состоит в следующем преобразовании: входной сигнал умножается на постоянную величину k, называемую коэффициентом усиления. Он может иметь любое действительное значение (положительное / отрицательное).
П ередаточнаяфункция:
W(P)
= k
(2.24).
ередаточнаяфункция:
W(P)
= k
(2.24).
Рис. 2.16. Выходная величина при скачкообразном изменении входной величины.
|
Звено |
ЛАЧХ |
ЛФЧХ |
|
Усилительное |
|
|
Графическое определение отклонения точкой ЛЧХ апериодического звена от асимптотического изображения.
Определение динамических ошибок с использованием коэффициентов ошибок.
Оценка качества системы при гармоническом воздействии.
Частотная характеристика колебательного звена и его графическая интерпретация.
Описание АФХ и ЛЧХ неустойчивых апериодического, колебательного, консервативного звеньев и звена неминимально- фазового типа.
Параметрические ошибки. Чувствительность.
теория инвариантности – один из основных разделов общей ТАУ, которая обосновывает синтез структуры и выбор параметров системы, находящейся под воздействием возмущений и помех.
Инвариантность какой-либо переменной САУ означает нечувствительность системы к действию возмущения.
При выполнении условий инвариантности достигается независимость регулируемой величины от внешних возмущающих воздействий и изменения параметров системы или точное воспроизведение управляющего воздействия.
Для достижения абсолютной инвариантности некоторой координаты x(t) относительно внешнего воздействия f(t) необходимо и достаточно, чтобы передаточная функция W(t) измерительного устройства была бы тождественно равна 0.
Динамический смысл условия абсолютной инвариантности, т.е. полной компенсации возмущений, заключается в том, что САУ воздействует на объект управления воздействием в точности равным внешнему воздействию на него, но противоположным по направлению.
Можно стремиться к достижению инвариантности одной из координат относительно внешнего возмущения или достижению инвариантности всех координат относительного одного какого-либо возмущения. Такие задачи называются задачами полиинвариантности.
Селективная инвариантность означает полную независимость / ограниченную зависимость установленной реакции системы на воздействие определённого вида.
Ковариантность переменных означает их совпадение/ близость.
Как отмечалось выше, изображение реакции y(t) на воздействие f(t) при нулевых начальных условиях записывается в виде: Y(s) = Ф(s)F(s), где Ф(s) – передаточная функция.
Реакция системы на воздействие имеет установившуюся и переходную составляющие, т.е. y(t) = yуст(t) + yпер(t). Характер установившейся составляющей определяется комплексным сектором изображения воздействия, переходной – полюсами передаточной функции системы.
Условие абсолютной инвариантности y(t) от воздействия f(t) записывается в виде s: Ф(s) = 0 (5.5) («квантор общности по s соответствует Ф(s) = 0»). Очевидно, что при этом не будет ни установившейся, ни переходной составляющих. Однако могут возникнуть свободные движения из-за ненулевых начальных условий.
Главной задачей для всей теории инвариантности в целом является проблема физического осуществления САУ, удовлетворяющей условию инвариантности.
В инженерной практике реализуется инвариантность до определённого уровня ε, т.е. ограниченная зависимость переменной от возмущающего воздействия.
Условие инвариантности до ε имеет вид: s: |Ф(s)| < ε > 0 (5.6).
Селективная абсолютная инвариантность достигается при обращении в 0 передаточной функции системы на спектре воздействий.
Если указано множество Ωf (Ω – омега), существенных частот воздействия, то селективная инвариантность до ε может быть количественно оценена по АФЧХ:
![]() ,
определяющей амплитуды установившихся
реакций на гармоническом воздействии
указанной частоты.
,
определяющей амплитуды установившихся
реакций на гармоническом воздействии
указанной частоты.
Очевидно, что переменная выхода системы ковариантна задающему воздействию, если соответствующая передаточная функция тождественна 1: s: Ф(s) = 1.
Теоретически ограничиваются рассмотрением только условий инвариантности переменных. Для следящих систем преимущественно использование ковариантности. Для систем стабилизации и подавления возмущений – условий инвариантности.
Кроме инвариантности при синтезе САУ большое влияние уделяется чувствительности системы.
Необходимым условием функционирования системы управления является малая чувствительность / параметрическая инвариантность их характеристик к вариациям элементов систем.
Для исследования влияния вариаций элементов на условие инвариантности системы используют функции чувствительности передаточной функции системы Ф(s).
Логарифмические
функции чувствительности записываются
в виде
![]() .
Позволяют оценивать относительное
влияние вариаций передаточных функций
элементовWi(s)
на передаточную функцию системы Ф(s).
.
Позволяют оценивать относительное
влияние вариаций передаточных функций
элементовWi(s)
на передаточную функцию системы Ф(s).
Обычно функции
чувствительности оценивают по их модулям
при s
= jω
(ω
≥ 0). Модули
функций чувствительности
![]() в виде частотных характеристик показывают
приблизительную зависимость относительных
приращений на каждой частоте.
в виде частотных характеристик показывают
приблизительную зависимость относительных
приращений на каждой частоте.
Помимо инвариантности и чувствительности при анализе САУ используют понятие «грубости». Система называется грубой, если малые приращения параметров не приводят к качественным изменениям её поведения. В линейных системах негрубость имеет место, если в результате малых изменений корни характеристического полинома переходят через мнимую ось.
Критерий Найквиста на плоскости ЛЧХ.
Для исследования устойчивости использую ЛЧХ. При этом критерий Найквиста для устойчивости в разомкнутом состоянии системы будет иметь следующую формулировку: замкнутая САУ будет устойчива, если ЛАХ её разомкнутого контура пересечёт ось частот раньше, чем ЛФХ достигнет –π.
Р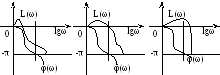 ис.4.17.
ЛХЧ устойчивой, находящийся на грани
устойчивости и неустойчивой САУ
ис.4.17.
ЛХЧ устойчивой, находящийся на грани
устойчивости и неустойчивой САУ
В случае использования ЛЧХ запас устойчивости по амплитуде определяется в точке пересечения ЛЧХ прямой (–π), запас устойчивости по фазе – на оси абсцисс.
Р ис.4.18.
Графическая интерпретация запаса
устойчивости системы по амплитуде и
фазе
ис.4.18.
Графическая интерпретация запаса
устойчивости системы по амплитуде и
фазе
При проектировании САУ рекомендуется назначать запас устойчивости по амплитуде ΔL ≥ 6 дБ, запас устойчивости по фазе Δφ ≥ 30°.
Метод исследования устойчивости с помощью ЛЧХ получим широкое распространение из-за простоты построения и наглядности ЛАХ и ЛФХ.
Результирующая ЛАХ незамкнутой САУ применяется не только для анализа устойчивости, но и даёт много другой информации о свойствах системы и часто используется на практике при синтезе САУ.
Все рассмотренные выше критерии устойчивости САУ равноценны, т.к. эти алгебраические критерии достаточно просты и могут быть поставлены на ЭВМ.
В некоторых случаях названные выше критерии, позволяющие получить аналитическое выражение для оценки устойчивости, накладывают ограничения на параметры системы, напрямую связанными с коэффициентами характеристического уравнения.
Одна алгебраические методы, применяются в случае, когда известно аналитическое выражение для коэффициентов характеристического уравнения.
Частотные критерии имеют основательную практическую базу и находят широкое применение на практике при проектировании новых моделей САУ, т.к. позволяют остаточно просто определить «физические характеристики САУ», т.е. полосу пропускания, резонансные частоты, сдвиг по фазе.
Геометрическая интерпретация корней характеристического уравнения.
Формулировка критерия Найквиста применительно к ЛЧХ.
Для исследования устойчивости использую ЛЧХ. При этом критерий Найквиста для устойчивости в разомкнутом состоянии системы будет иметь следующую формулировку: замкнутая САУ будет устойчива, если ЛАХ её разомкнутого контура пересечёт ось частот раньше, чем ЛФХ достигнет –π.
Р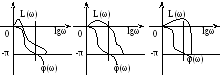 ис.4.19.
ЛХЧ устойчивой, находящийся на грани
устойчивости и неустойчивой САУ
ис.4.19.
ЛХЧ устойчивой, находящийся на грани
устойчивости и неустойчивой САУ
В случае использования ЛЧХ запас устойчивости по амплитуде определяется в точке пересечения ЛЧХ прямой (–π), запас устойчивости по фазе – на оси абсцисс.
Р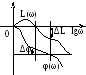 ис.4.20.
Графическая интерпретация запаса
устойчивости системы по амплитуде и
фазе
ис.4.20.
Графическая интерпретация запаса
устойчивости системы по амплитуде и
фазе
При проектировании САУ рекомендуется назначать запас устойчивости по амплитуде ΔL ≥ 6 дБ, запас устойчивости по фазе Δφ ≥ 30°.
Метод исследования устойчивости с помощью ЛЧХ получим широкое распространение из-за простоты построения и наглядности ЛАХ и ЛФХ.
Результирующая ЛАХ незамкнутой САУ применяется не только для анализа устойчивости, но и даёт много другой информации о свойствах системы и часто используется на практике при синтезе САУ.
Все рассмотренные выше критерии устойчивости САУ равноценны, т.к. эти алгебраические критерии достаточно просты и могут быть поставлены на ЭВМ.
В некоторых случаях названные выше критерии, позволяющие получить аналитическое выражение для оценки устойчивости, накладывают ограничения на параметры системы, напрямую связанными с коэффициентами характеристического уравнения.
Одна алгебраические методы, применяются в случае, когда известно аналитическое выражение для коэффициентов характеристического уравнения.
Частотные критерии имеют основательную практическую базу и находят широкое применение на практике при проектировании новых моделей САУ, т.к. позволяют остаточно просто определить «физические характеристики САУ», т.е. полосу пропускания, резонансные частоты, сдвиг по фазе.
Критерий устойчивости линейной системы.